ВИЩЕ ПРОФЕСІЙНЕ УЧИЛИЩЕ №20

м. Львова

 

 

 

 

 

 

 

 

 

 

 

 

 

 

МЕТОДИЧНІ ВКАЗІВКИ 

 

до виконання практичних робіт у програмі Maple

 

 

 

 

 

 

Розробив: викладач інформатики та спецдисциплін 

Бідак І.О.

 

 

 

 

Львів 2017

Методичні вказівки розроблені для виконання практичних робіт у програмі Maple. Ця програма допоможе учням при вивченні математики рівня середньої школи та деяких розділів вищої математики, що входять у програму з математики у спеціалізованих школах та ПТНЗ. Методичні вказівки допоможуть швидше зрозуміти сутність абстрактних понять математики, а також побачити складні графіки функцій, які важко зобразити на площині.

Теоретичні відомості.

 

1.Система комп’ютерної алгебри Maple версія 5.0 або 7.0

 

 Це потужний пакет, призначений для розв’язку різноманітних математичних задач. Процедурного програмування розв’язку задач лінійної алгебри та математичного аналізу.

           

Можливості системи:

 

1.      Розв’язок лінійних, нелінійних рівнянь, нерівностей, системи рівнянь та нерівностей.

2.      Обчислення звичайних математичних функцій (sin,cos,log, e^x і т.д. ). 3. Диференціальне та Інтегральне числення. Розв’язок диференціальних рівнянь.

4.      Операції над матрицями, векторами (Визначник, матричний і векторний добуток, обернена матриця і т.д.).

5.      Побудова графіків двомірних і тримірних функцій.

6.      Складання програм у вигляді процедур для розв’язку математичних задач.(Наприклад знаходження точок екстремуму функції).

 

Вікно програми  Maple V 7.0. Елементи вікна.

 

 

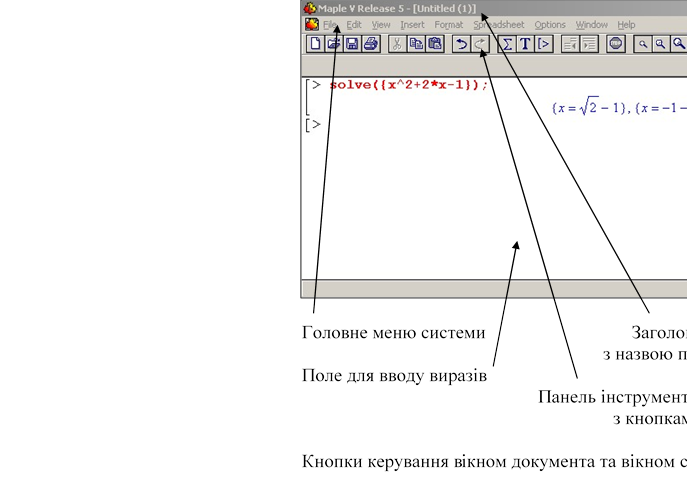
Приклад запису функції для розв’язку квадратного рівняння записаний у полі документа. 

Відповідь виведена системою у наступному рядку.

1.1. Меню системи.  

 

          Меню подібне до стандартного меню будь-якої програми (Напр. Word). Лише починаючи з третього пункту команди суттєво відрізняються.

 

 

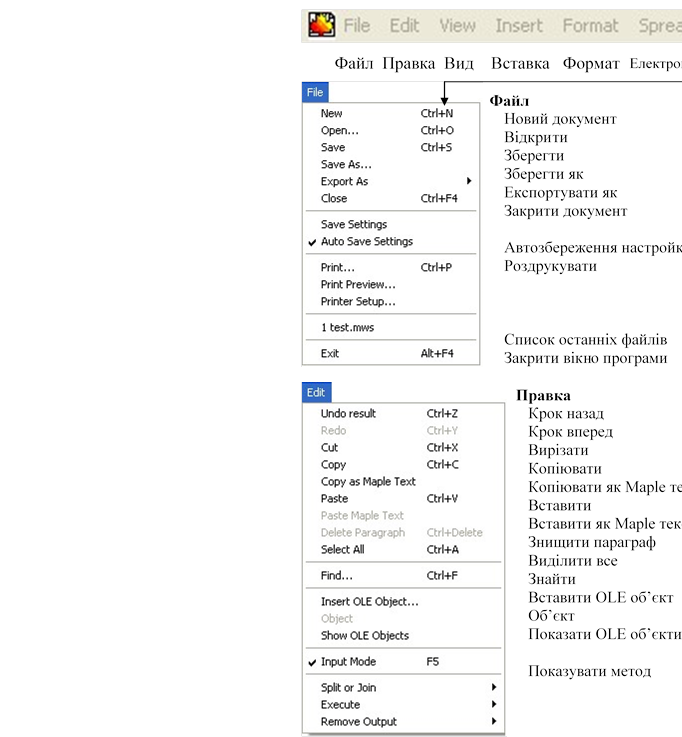
Команди, які не описані, не є основними. Тому при роботі початківці їх практично не використовують. У меню є групи команд, які представляють режими роботи. Режим може бути увімкнений або відключений. Якщо навпроти команди стоїть позначка (прапорець) то режим увімкнений. Вимкнути режим можна за допомогою лівої клав. миші, клікнувши на прапорці.

 

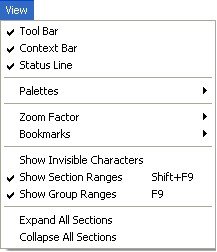
  Вид 

Панель інструментів 

Контекстна панель

Рядок статусу

 

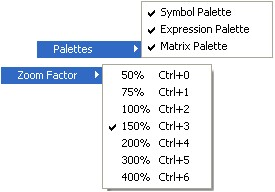
Палітри 

Вибір масштабу 

 

 

 

 

 

 

 

Символьна палітра (Symbol Pallete)  використовується для вводу математичної символіки грецькими буквами

 

 

 

 

 

 

Палітра виразів (Expressions Pallete)          

 

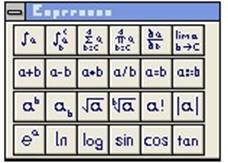
використовується для швидкого вводу виразів за шаблоном, зображеним у кнопці

 

 

 

 

 

Палітра матриць (Matrix Pallete)

 

використовується для швидкого вводу матриць та векторів до четвертого порядку

 

 

 

 

 

 

 Більшість основних команд, що знаходяться у пунктах меню винесені на панель інструментів у вигляді кнопок. Їх достатньо для роботи користувача.

Настройки  вікна (інтерфейсу) стандартні і змін не потребують.

1.2. Панель інструментів Maple 7.0

 

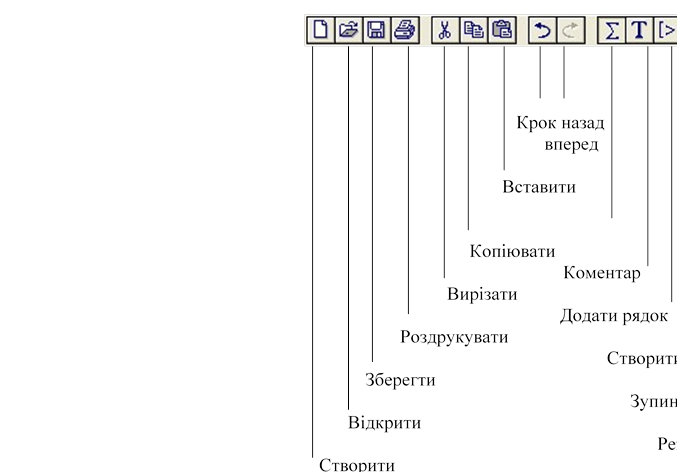
    Документ                                                                     Оптимальні розміри вікна

 

 Не усі кнопки на панелі активні. Це означає що для виконання даної дії потрібно виділити текст, або увімкнути відповідний режим. Під панеллю інструментів розташована “Контекстна панель” (Context Bar). Вона містить такі кнопки:

 

Для зручності користувач обирає які панелі інструментів йому потрібні на даний момент, а які зайві і їх потрібно забрати з робочої області вікна системи.

 

 

2. Запис та обчислення виразів у системі Maple 7.0

 

Maple – має свій алфавіт, який складається з :

ü 52 символів (26 латинських малих букв і 26 лат. великих);

ü цифр від 0 до 9;

ü спеціальних символів {} , [] ; : # ^ () . +  – * / =

Вирази записуються  на специфічній мові, назви стандартних функцій такі самі як у англійській мові, тільки у скороченому варіанті. Правила запису математичних виразів близькі до мови Pascal. Оператор присвоєння, конструкції розгалуження та циклу дають можливість програмувати задачі у вигляді процедур.

 

Запис у математиці	Запис у системі Maple
додавання + віднімання                             - ділення                                   / корінь квадратний               a піднесення до степеня         x3 дорівнює                                = модуль числа                        |x| x2y	+ – / sqrt(a) x^3 = abs(x)

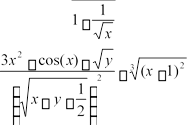(x+2*y)/(1+1/sqrt(x))

(3*x^2+cos(x)-sqrt(y))/sqrt(x+y1/2)^2+(x+1)^(2/3)

 

 

2.1. Оператор присвоєння. Обчислення математичних виразів. 

 

Оператор присвоєння працює аналогічно як у мові Паскаль. Змінним присвоюються числові значення або математичні вирази зі змінними величинами. Бажано у одному документі використовувати декілька змінних. Щоб їх не плутати, можна проіндексувати їх імена. 

Наприклад: для системи рівнянь: х1+х2+х3=2,  х1,х2,х3 – змінні, а числа у кінці х – це у нашому випадку індекси. Разом буква і цифра складають ім’я змінної (х1,х2,х3 і т.д).

 

Приклади обчислення математичного виразу:

 

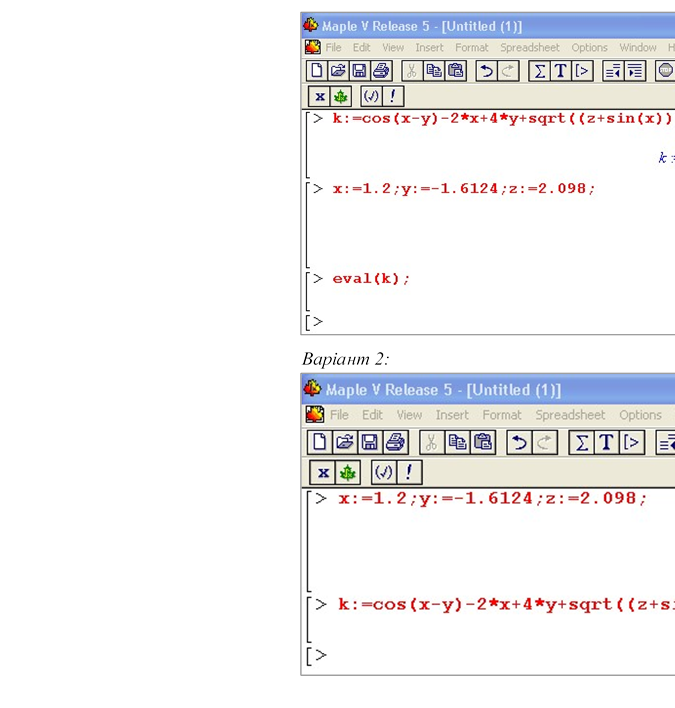
Варіант 1: 

а) введення виразу та присвоєння його змінній k;

б) присвоєння змінним x, y, z числових значень;

в) запис функції eval(k) для обчислення виразу k . Варіант 2: 

а) присвоєння змінним x, y, z числових значень;

б введення виразу та присвоєння його змінній k.

Варіант 1:

2.2. Розв’язок лінійного та квадратного рівняння з одною змінною. Система рівнянь.

Для розв’язку рівнянь використовують функцію solve. Загальний вигляд функції:  solve(рівняння);

 

Наприклад: Варіант 1:

а) присвоїти рівняння змінній;

б) записати функцію solve, використовуючи змінну.

 

Варіант 2:

Записати рівняння безпосередньо у функції solve.

Варіант 1:

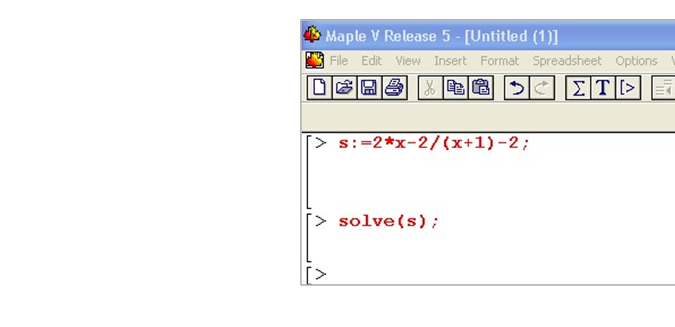Оскільки при зведенні до спільного знаменника лінійне  рівняння перетвориться у квадратне, то розв’язків буде два.                  розв’язки 

 

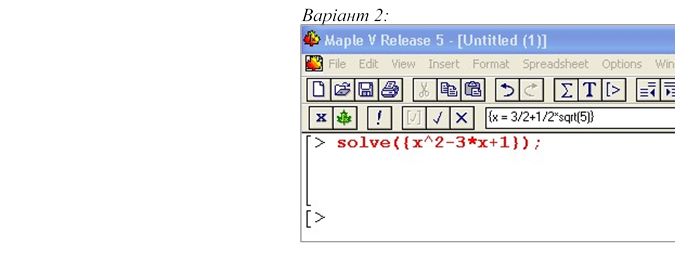
Якщо рівняння записати у фігурних дужках { }, то результат буде таким

 

Розв’язок системи рівнянь записують аналогічно, тільки кожне рівняння у дужках розділяють комою.

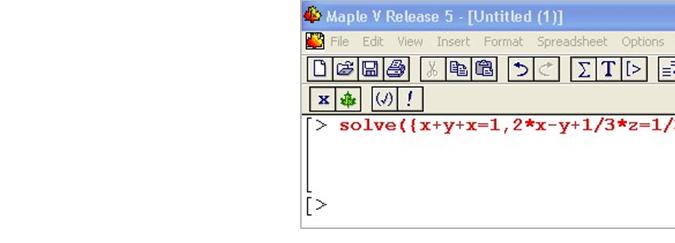
Результат

2.3 Знаходження похідної. Частинна похідна.

 

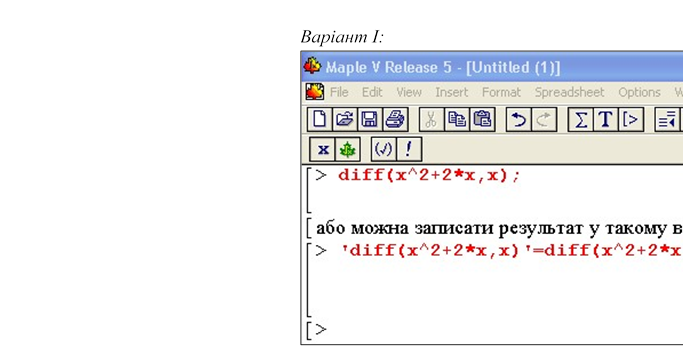
Для знаходження похідної функції (або диференціал) використовують функцію diff(). Загальний вигляд функції:

 

diff(математична функція, аргумент); де

математична функція – математичний вираз,                         аргумент – аргумент відносно якого береться похідна.

 

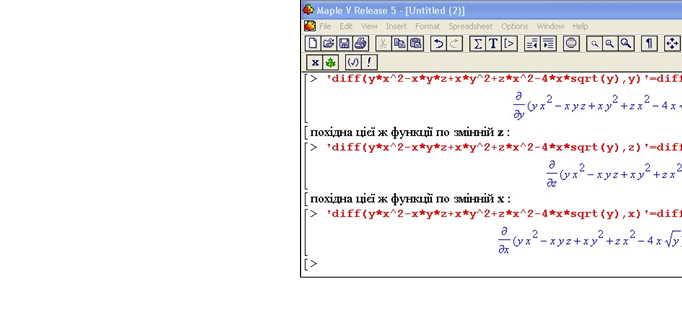
Якщо потрібно знайти частинну похідну від функції двох і більше змінних, вказують змінну відносно якої шукають похідну цієї функції.

 

Приклад 1. “Похідна від функції одної змінної” :

 

 

 

 

2.4. Знаходження неозначеного та означеного інтегралу.

 

Неозначений інтеграл – це первісна від функції. Означений інтеграл – це різниця між первісною функції у верхній межі і первісною функції у нижній межі. Отже результатом означеного інтегралу буде функція (точніше це первісна від підінтегральної функції), а результатом означеного інтегралу буде числове значення.

 

x3dx

^ _42xx2 ; – неозначений інтеграл,

 

2 x2dx

                          ^ 4_x₂ ^;      – означений інтеграл.

_0.5  

Для обчислення таких інтегралів використовують функцію int(); Загальний вигляд функції: int(вираз,x=a..b); для неозначеного: int(вираз,x) де  вираз – підінтегральна функція,

              a,b – нижня і верхня межі інтегрування,         x – змінна інтегрування.

 

          Щоб результат було зручно читати, використовують прирівнювання виразу до функції, як це було у розділі обчислення похідної (диференціалу) функції.

           

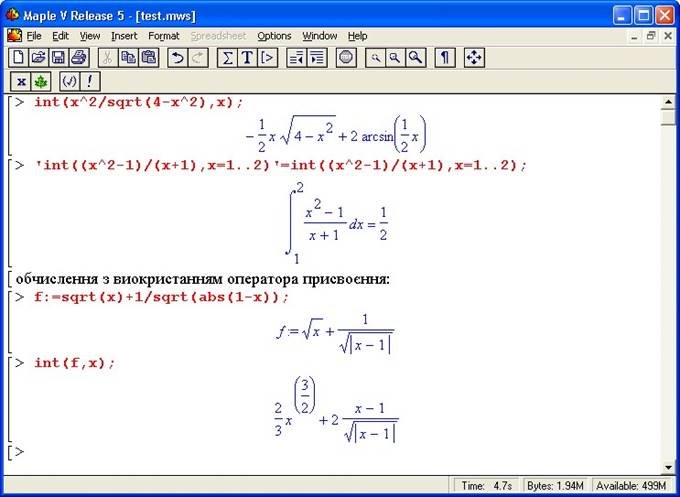
         ’int(x^2/sqrt(4-x^2),x=-0.5..2)’= int(x^2/sqrt(4-x^2),x=-0.5..2);

 

результат виконання такого запису зображений на малюнку:

 

           

Також можна використовувати інші варіанти запису та обчислення означеного або неозначеного інтегралу:

 

 

 

 

 

2.5. Обчислення границь.

 

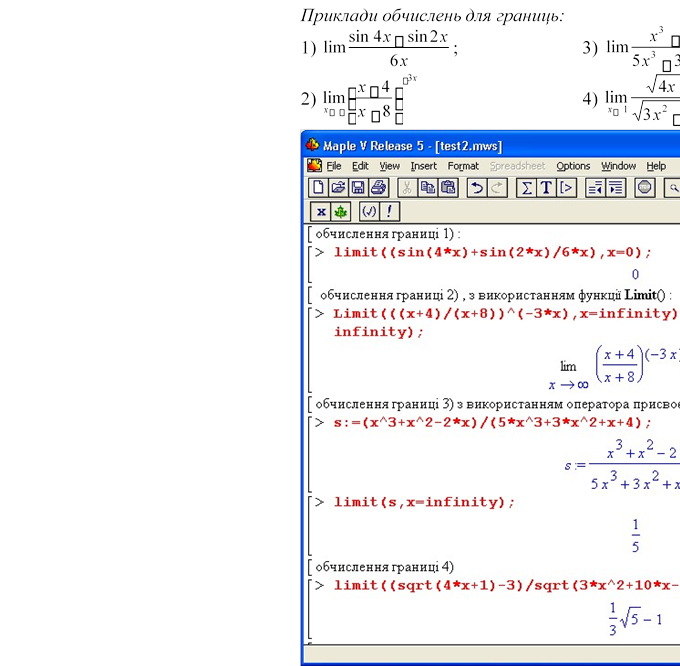
Для обчислення границь у системі Maple використовують використовують функцію limit(вираз, аргумент), (Такий запис: Limit(вираз, аргумент) дає можливість лише зручніше показати запис границі користувачу. Ця функція не виводить результат).

 

де  вираз – функція для якої шукатимуть границю,

 

аргумент – змінна функції і значення до якого прямує ця змінна.

 

 

Обов’язково аргумент прирівнюється до значення, до якого прямує змінна функції. Приклад запису: limit(sin(x)/x, x=0);

 

x0                                                                                                                                                                                                                               x

3. Побудова графіків у системі Maple

 

Система дозволяє будувати двомірні і тримірні графіки функцій. Графіки функцій можуть мати різноманітний вигляд, завдяки функціям представлення. Змінити вигляд графіка можна за допомогою кнопок на панелі інструментів, яка з’явиться лише тоді, коли відмітити графік мишею.

 

 

 

3.1. Побудова двомірних графіків

 

          У системі Maple двомірні графіки будуються за допомогою функції plot(). Загальний вигляд функції: plot(вираз, параметр)

 

де      вираз – це математична функція одної змінної. Записують як звичайний математичний вирах у системі Maple;

           

параметр – це проміжок осі абсцис, на якій будуватиметься графік. Проміжок

вибирається користувачем довільно, у наперед передбачуваних межах.

 

Приклади запису функції plot() для побудови графіків функцій :

 

1) x² 1;     3) 51n(x1)cos²(x1) 2) sin13x; 4) sin(5x)ctg(x)

 

(проміжок вибирається користувачем)

 

зображені на малюнку: 

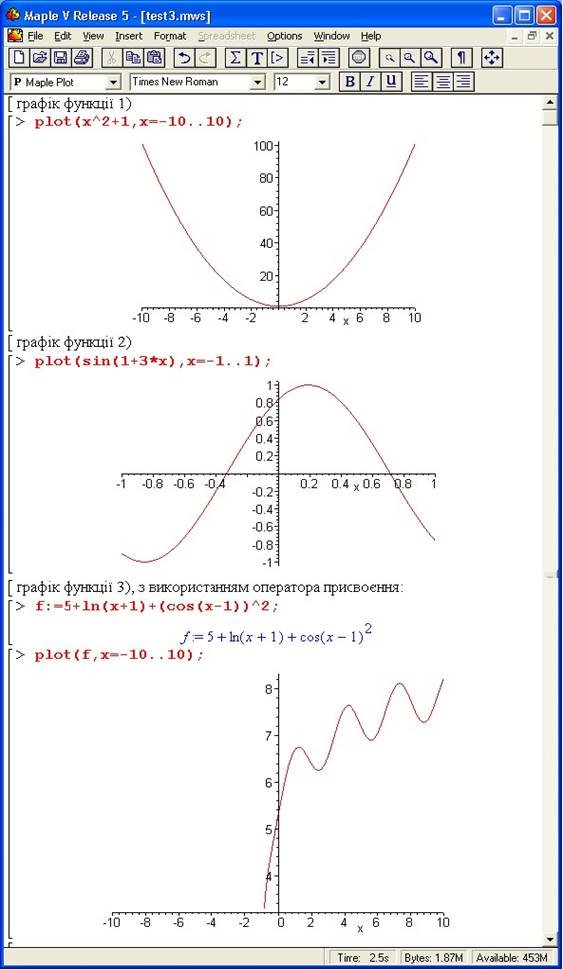
Зображення графіку функції 4) у різних режимах представлення:

 

 

 

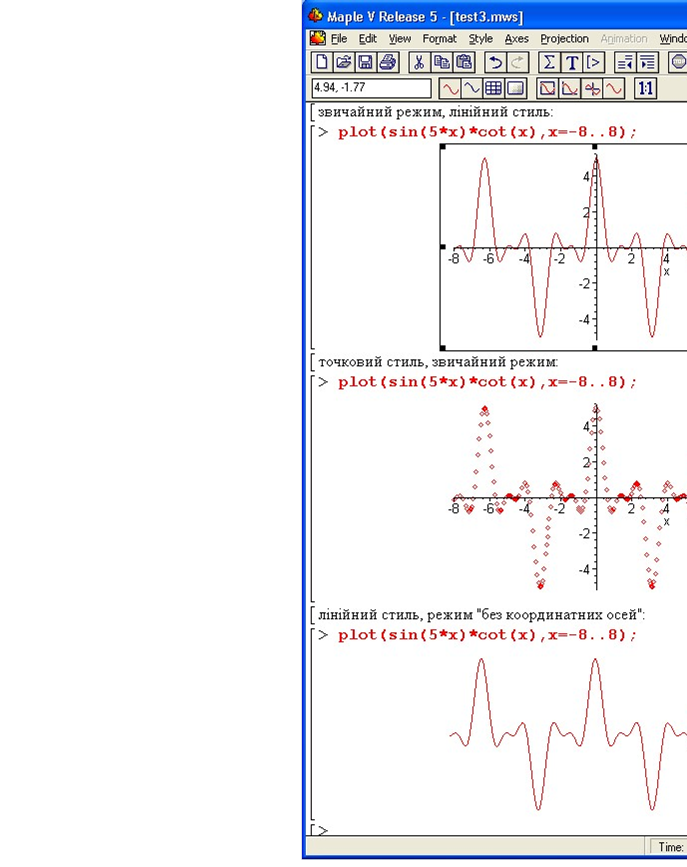
Кожна група кнопок на панелі інструментів працює у режимі вибору. Групи працюють незалежно. Але лише одна кнопка у кожній групі може бути натисненою.

 

3.2. Побудова тримірних графіків

 

У системі Maple тримірні графіки будуються за допомогою функції plot3d(). Загальний вигляд функції: plot3d(вираз, параметр1,параметр2) де      вираз – це математична функція двох змінних. Записують як звичайний математичний вирах у системі Maple;

параметр1,параметр2  – це проміжки осі абсцис і осі ординат, на яких будуватиметься графік. Проміжок вибирається користувачем довільно, у наперед передбачуваних межах.

 

Приклади запису функції plot3d() для побудови графіків функцій:

 

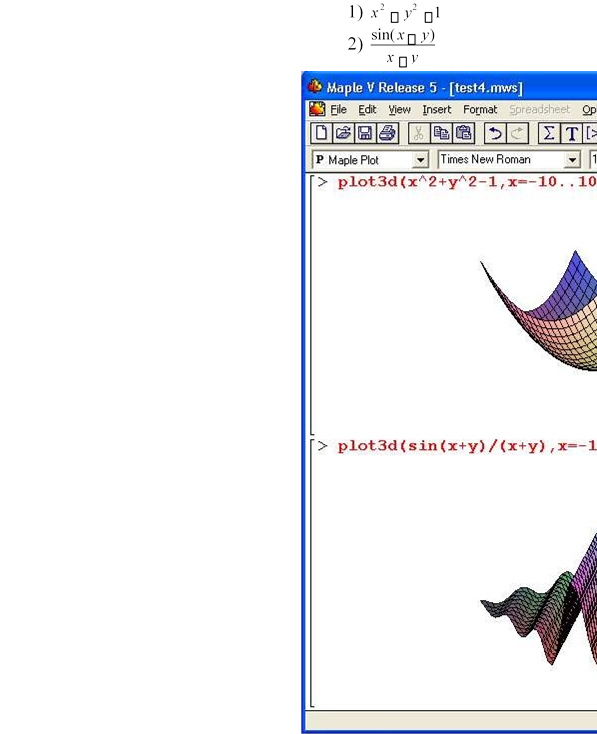
 Система дозволяє побачити графік з різних сторін. Графік можна обертати, використовуючи панель інструментів або використовуючи ліву клавішу миші. Клікнувши на графіку мишею, з’явиться рамка – область графіка. При натисненні у русі лівої кл. миші. графік буде обертатися. Щоб зафіксувати положення, потрібно відпустити лів. кл.  миші.

 Можна змінювати вигляд і стиль зображення фігури, так як у двомірному графіку. Панель інструментів маніпулювання тримірним графіком виглядає так

 

 

 

  1442443 1142434244546 7 8₁₄9₄₂10₄₄₃11 ₄₃

 

                координати фігури             стилі зображення фігури         вигляд системи 

координат

 масштаб один до одного      

 

Приклад 1: вигляд фігури з різних точок системи координат

 

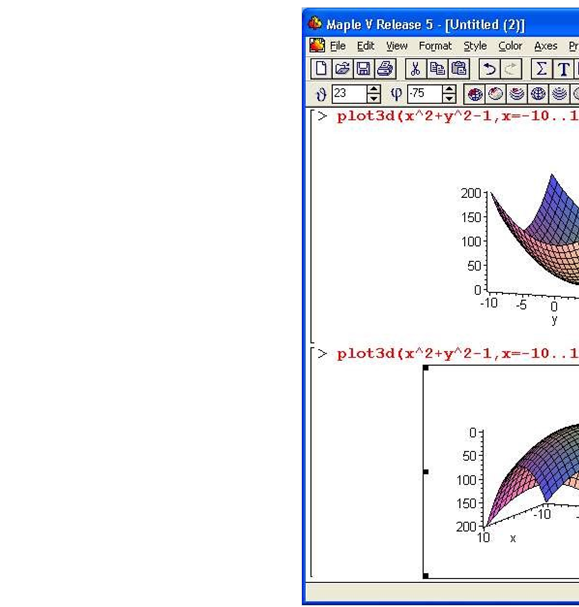
Приклад 2: стиль зображення фігури та вигляд системи координат

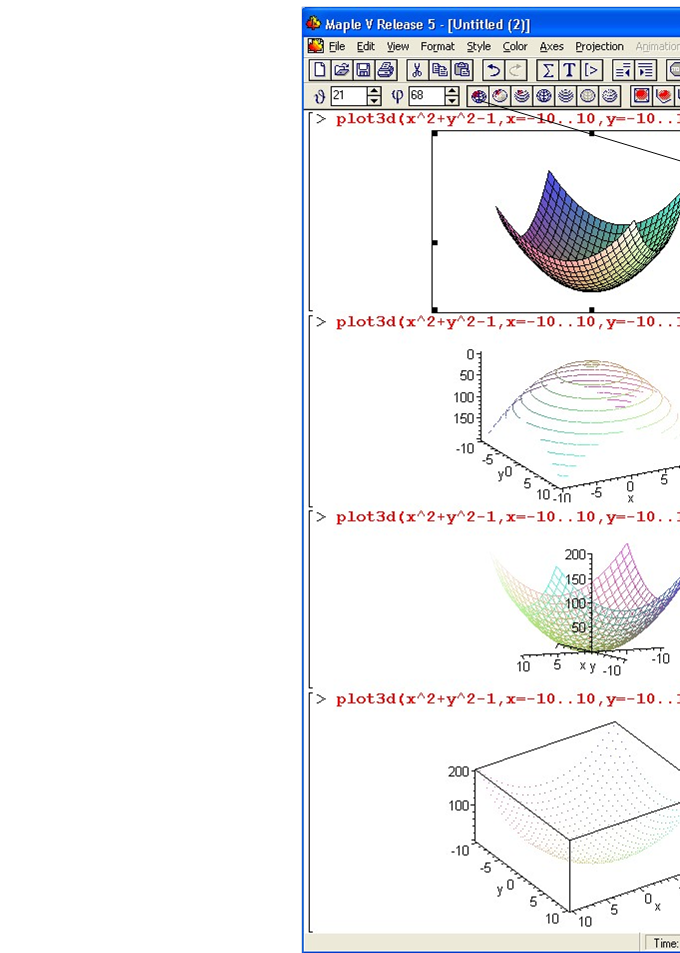
4. Обчислення лінійної алгебри 

 

 Система має багато функцій для лінійної алгебри. Це функції, які обчислюють визначник матриці, добуток або суму матриць векторний добуток, обернену матрицю, градієнт, і багато інших величин.

Для проведення обчислень потрібно спочатку підключити пакет лінійної алгебри linalg. Після підключення система виводить назви усіх функцій, які можна використовувати для лінійних обчислень:

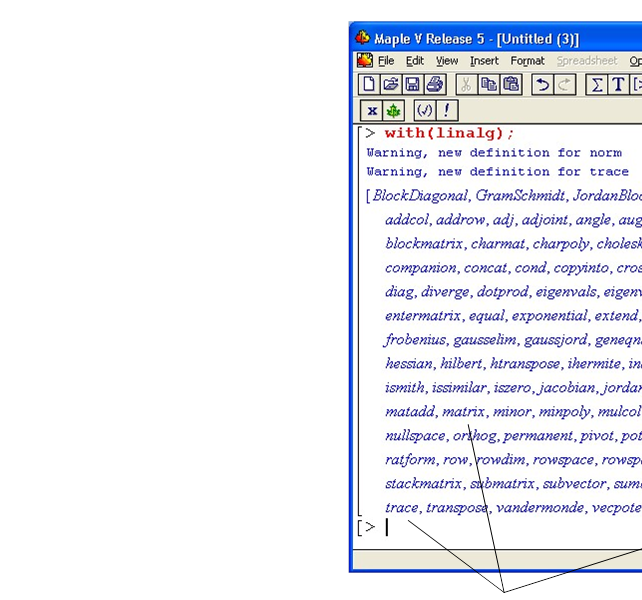
                   назви функцій лінійної алгебри

 

Пакет потрібно підключити лише раз, на початку роботи або безпосередньо перед написанням функцій лінійної алгебри. Інакше система буде видавати помилку запису функції. Оскільки основи лінійної алгебри вивчають у вищій школі і користувач може не володіти повною інформацією про функції, терміни, величини лінійної алгебри, тоді можна використовувати довідкову систему Maple. Як користуватися довідкою системи дивіться параграф 5.

 

 

4. 1. Запис матриці, обчислення визначника. 

 

 Матриця – це прямокутна таблиця з елементами, кожен з яких має індекси, які вказують на місце елемента у таблиці. 

Елемент матриці a_{i j} , де i – номер рядка, j – номер стовпця у якому знаходиться елемент. Ми будемо розглядати лише квадратні матриці nm, тобто такі де кількість рядків і стовпців однакова (nm). 

 

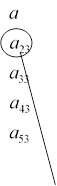
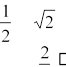               a11 a₁₂                 13 a14 a15                                     1         



                            a₂₁ a₂₂a₂₄ a25                                                    

Aa₃₁ a₃₂a₃₄ aa35₄₅                                         D 413 2012,5 32 __

a41 a₄₂a₄₄

             a₅₁ a₅₂                      a₅₄ a55                                  0     

 

 

елемент другого рядка і         матриця 33 з елементами третього стовпця (i  2, j  3)

 

Елементами матриці можуть бути дійсні числа (додатні, від’ємні, дробові, натуральні, раціональні і т.д. ) або змінні величини (символи). Матриці позначають великими буквами, усі елементи зображають у дужках, як показано вище.

Визначник – це число. Визначник позначають так A – визначник матриці А.

Визначник матриці 22 і 33 можна легко порахувати, не використовуючи системи, за таким правилом:

 1) правило для матриці  22:

                         1     2 

              A  _4 _7_; | A|1(7)24  15;

_

2) правило для матриці  33(правило трикутників):

 

крок 1

                               (2)25113(4)(1)1 13

                     

 

 

 

_{крок 2} 1231(4)51(1)(2)  12

                     

 

крок  3 

                     

Найчастіше результат обчислень записують так:

 

A (2)25113(4)(1)11231(4)51(1)(2)  1312  1

 Обчислити визначник четвертого і вищого порядку набагато складніше, тому зручно використати систему Maple. Для вводу матриці використовують функцію matrix(n, m, [[a1,a2, .., ],[], … []]); де n, m – розміри матриці ( кількість рядків і стовпців),     [[a1,a2, .., ],[], … []] – елементи матриці, записані по рядках.

 

Приклад обчислення визначників матриць:

 

                1   1   2                                   1 2 4          2 

13  02,5 23  2) B 00 94 73 312 1)  A

                0       5     2                                  4 8 3 1 

                                       

 

 

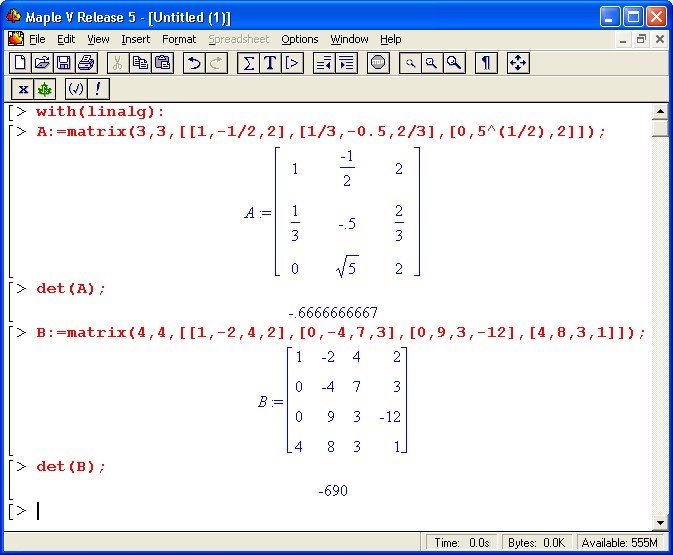
 Функція під єднання пакету лінійної алгебри записана з двокрапкою у кінці. Це дозволяє підключити пакет, але не виводити інформації про набір функцій, якими можна користуватись. Якщо не потрібно показувати результати обчислень на екрані, то потрібно ставити “:” у кінці записаного рядка чи функції.

5. Довідкова система Maple

 

          Довідкова система має ієрархічну (деревоподібну) структуру. Довідку можна викликати з меню системи: Help => Help On “Maple”. Підменю Help має декілька пунктів:

 

 

Проглянути вступ до Maple

Допомога по Maple

Турне для нового користувача

Що нового 

Використання довідки

Пошук за темою 

Повний текстовий пошук 

Історія 

Запис до бази даних 

Змінити тему 

 

Спливаюча підказка

Про Maple V

 

 

Кожен з цих пунктів виводить спосіб подання довідки для користувача. Способи бувають різні:

 

ü можна перечитувати повністю довідку від початку до кінця (використовують пункт Help on “Maple”), 

ü переглянути для чого призначена програма (introduction), послідовно продивитися можливості та приклади роботи з Maple (New User's Tour), 

ü прочитати про нові можливості Maple V 5.0.(What’s New), 

ü пошук з використанням ключового слова або теми (Topic Search), 

ü пошук з використанням фрагменту або речення у тексті (Full Text Search), 

ü список використання довідки (History),

ü змінити тему для пошуку (Remove Topic),

ü увімкнути/вимкнути спливаючу підказку (Balloon Help),

ü загальна інформація про Maple (About Maple V).

 

Вікно довідки відкривається паралельно з робочим вікном. Це вікно має кнопки керування та смуги прокручування, панель інструменті для зручнішого перегляду тексту у довідці, списки з розділами і підрозділами. У довідці можуть бути кнопки  відкриття/закриття     /       розділу для перегляду, гіпертекстові посилання на ключові слова.

Досить зручно використовувати довідку безпосередньо використавши її з робочого вікна. Спочатку потрібно ввести знак “?” , а тоді написати назву функції для якої потрібна довідка і натиснути <Enter>. Причому назва може бути неповна, лише 3-4 перші символи. Наприклад:

                           ] > ?int        це виклик довідки для функції інтегрування.

Звичайний виклик довідки з меню Help, пункт Help Guide:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

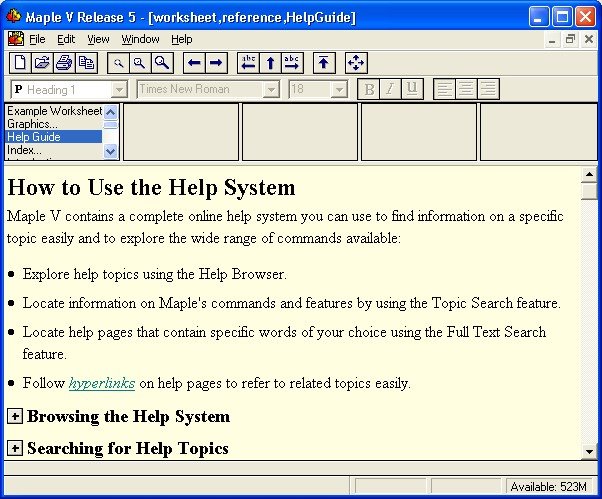
Виклик довідки за назвою функції:  ?int

 

 

 

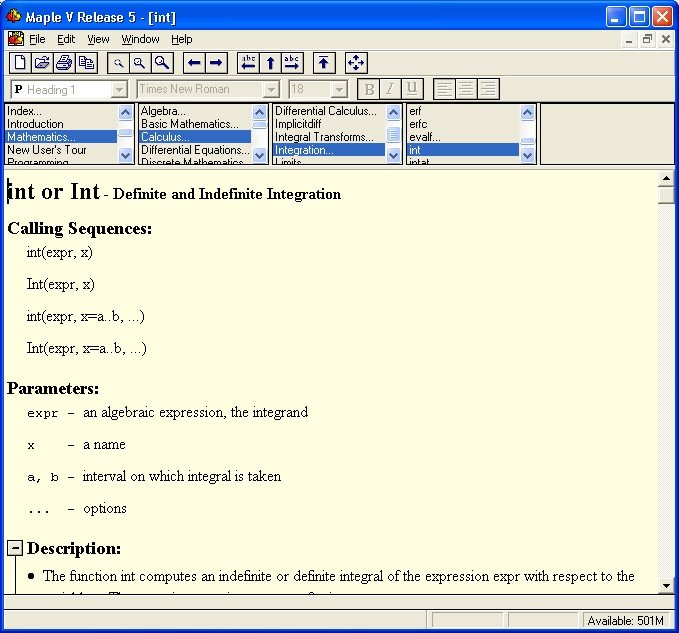
6. Нове середовище Maple 2016 для Windows 7/8/10 (32/64 біт)

 

Новий інтерфейс Maple 2016 – це нові можливості для користувача. Тепер можна виконувати математичні операції та обчислення не знаючи мови запису виразів. Викликавши контекстне меню на введеному прикладі/виразі ми отримуємо список дій у вигляді контекстного меню з підказками і прогнозованим результатом. Система вже давно вийшла за межі звичайної математики, тепер тут поєднані такі предмети як: 

ü природничі науки (фізика, хімія), 

ü нарисна геометрія, побудова графіків функцій,

ü лінійна алгебра та програмування,

ü математична статистика і  ймовірність, 

ü дискретна математика,

ü економічні задачі та методи оптимізації,

ü дослідження сигналів та шуму,

ü дослідження кривих, ü теорія чисел та фрактали, ü теорія графів та логіка.

На стартовій сторінці одразу можна ознайомитися з можливостями системи, скориставшись відповідними піктограмами:

 

 

 

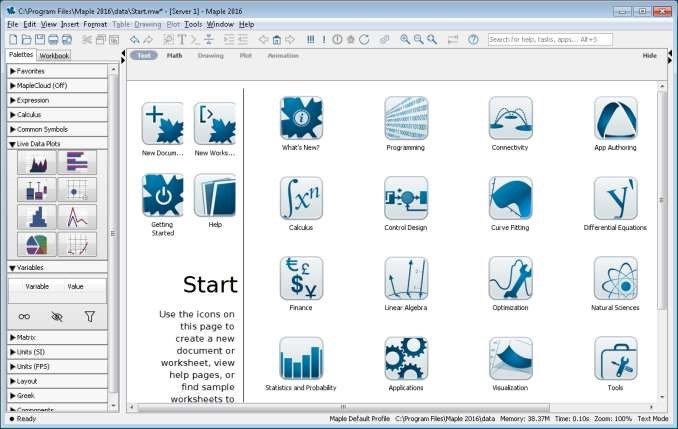
Нові функції програми 2016-го року можемо дізнатися натиснувши кнопку  

 

 

 

Детальніший опис можливостей  версії програми 2017 року можна побачити і оволодіти навичками, переглянувши вебінар за посиланням: https://www.youtube.com/watch?v=pcRS6mwGDgc

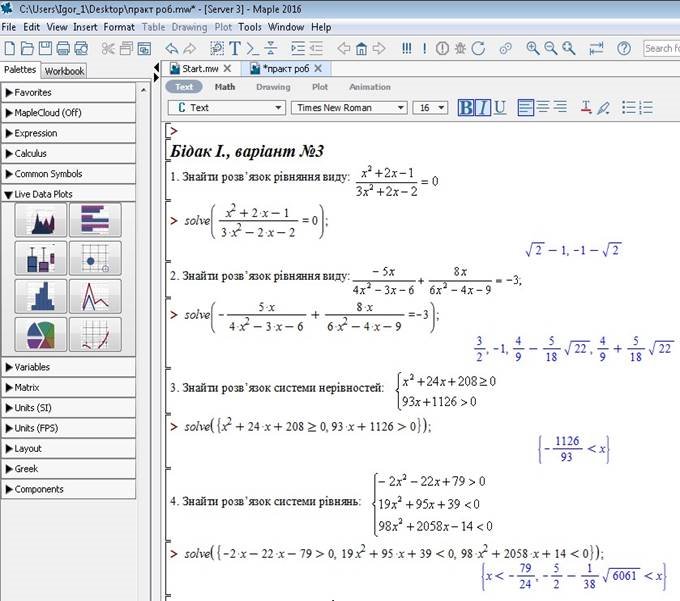
7. Приклад виконання практичної роботи у середовищі Maple 2016

 

Завдання для практичної роботи

з предмета «Інформатика та обчислювальна техніка», тема «Система комп’ютерної алгебри Maple»,

для спеціальності «Зварювальне виробництво» (молодший спеціаліст)

 

Варіант 3

1.     Знайти розв’язок квадратного рівняння: (6x² 21x25)(8x² 28x11) 90;

2.     Знайти розв’язок квадратного рівняння:   ₂^5x      ₂ ^8x   3;

                                                                                                                                4x 3x6         6x 4x9

3.     Знайти розв’язок системи нерівностей:  ^_^{x2 24x 208 0}

_93x1126  0

2x² 22x790

4.     Знайти розв’язок системи нерівностей:  ^_19x² 95x390

^98x² 2058x140

 Знайти границю:  lim 2xx²26₁₁x_x_5₅; 5.

                                                                 x        1              _

1 ² 2x2

6.                                                                                                                           Знайти похідну функції:  x 

3

7.                                                                                                                           Обчислити неозначений інтеграл: ^_x^₂²_^x_6x^5_^dx₁₃;

1

8.                                                                                                                           Обчислити означений інтеграл:  sin x1dx.

0

                                                                                                                   2          1                1

1^

9.                                                                                                                           Розв’язати показникове рівняння: ^{5 x} 5^x  24^x  0

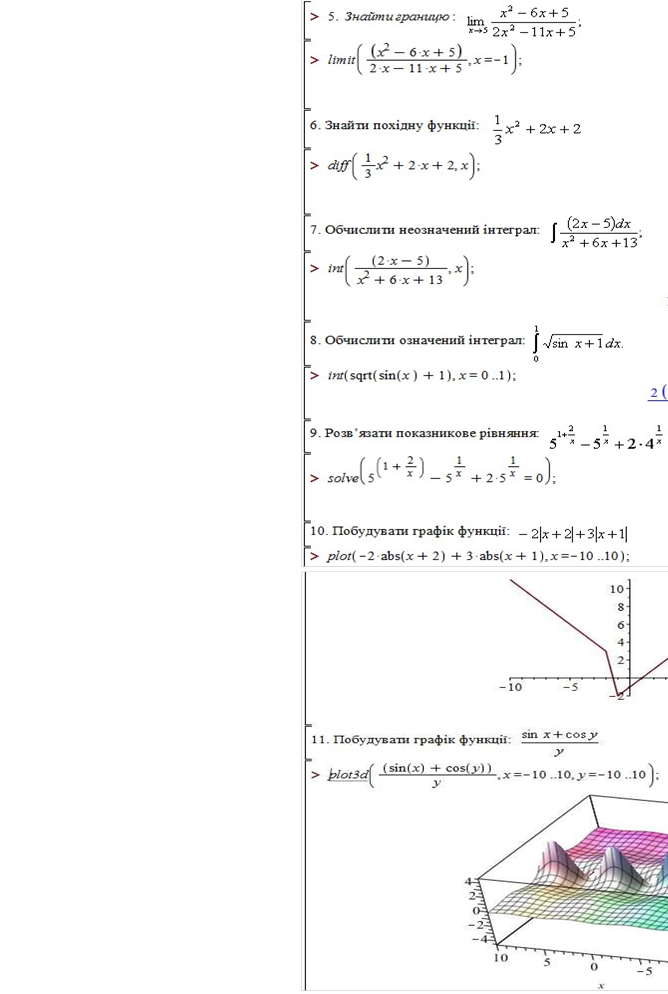
10.                                                                                                                      Побудувати графік функції:  2x23x1

11.                                                                                                                      sinxcos y

Побудувати графік функції:

 1   2  1 12. Обчислити визначник матриці:  1

1 2

0 3 1

3  0   5

y

                                                                                                                                _

  0 

0

2 7

2

 

 

 

Дані можна вводити звичним методом, знаючи мову запису або заготовленими шаблонами, що розташовані на палітрі інструментів зліва у вікні програми.

 

 

 

 

 

Переглянувши вебінар за посиланням:

https://www.youtube.com/watch?v=pcRS6mwGDgc можна побачити детальніший опис можливостей версії програми 2017 року а також оволодіти початковими навичками роботи у новому середовищі.

 

 

Список рекомендованої літератури 

 

1.     Білоусова Л.І., Горонескуль М.М. Курс вищої математики у середовищі Maple:

Навчальний посібник. – Х.: УЦЗУ, КП "Міська друкарня", 2009. – 412 с.

2.     Махней О. В. Математичне забезпечення автомати- зацiї прикладних дослiджень: навчальний посiбник / О. В. Махней, Т. П. Гой. – Iв.-Франкiвськ:

Сiмик, 2013. 304 с.

3.     Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч.1. - Харків: ХНУРЕ; Фактор, 2004. – 592 с.

4.     Кушнір В.А. Технологія бінарних занять з диференціальних рівнянь і інформатики у ВНЗ на основі Maple-середовища // Інформаційні технології в освіті. – 2016. – № 25. – С. 7-26

5.     Кушнір В.А. Проблеми поєднання фундаментального і інноваційного при вивченні математики у вищих навчальних закладах // Витоки педагогічної майстерності: Зб. наук. праць / Полт. педаг. універ. ім.В.Г.Короленка. – Полтава, 2015 С. 161 – 172.