системи рівнянь з двома змінними

                                          Урок №

                                   (алгебра 9 клас)

Тема уроку: системи двох рівнянь з двома змінними, як математична модель текстових і прикладних задач

Мета уроку: застосування систем двох рівнянь для прикладних задач

Тип уроку: комбінований

Наочність і обладнання: задачі зі збірника

Хід уроку

1. Перевірка домашнього завдання, опитування про основні методи розв’язання систем рівнянь другого степеня з двома змінними.
2. Повторення вивченого матеріалу.

Фронтальна бесіда.

Які основні типи текстових задач ви знаєте?

На рух, на рух водоймою, на спільну роботу, на переливання, на сплави і суміші, на відсотки, на складання рівнянь.

3. Формування знань

Алгоритм розв’язку прикладних задач

1. Проаналізувати  умову задачі (основні величини, зв’язки між ними, вимоги задачі)
2. Створити математичну модель( у вигляді тексту, рисунку, таблиці, тощо)
3. Скласти систему рівнянь до задачі
4. Розв’язати отриману систему рівнянь
5. Проаналізувати отримані результати на  з огляду на умову задачі
6. Записати відповідь

Застосуємо даний алгоритм для розв’язування задач

Задача 1

За 5кг цукерок і 4 кг печива заплатити 310 грн. Скільки коштує 1 кг цукерок і скільки 1 кг печива, якщо 3 кг цукерок дорожчі за 2 кг печива на 76 грн.

Розв’язання

Нехай 1 кг цукерок коштує x грн, а 1 кг печива Тоді за 5 кг цукерок і 4 кг печива заплатили 5x+4y=310 (грн). 2 кг печива коштують 2y  грн, а 3 кг цукерок коштують  3x грн, що за умовою на 76 грн дорожче, отже, 3x-2y=76 (грн). Маємо:     Додавши рівняння останньої системи отримаємо: 11x=462, x=42. Тоді 210+4y=310; y=25

Відповідь: 42 грн, 25 грн.

Задача 2

Вкладник поклав до банку на два різні рахунки 12000 грн. По першому з рахунків банк виплачує 6% річних, а по другому 8% річних  Через рік клієнт отримав 800 грн відсоткових грошей. Скільки гривень він поклав на кожен рахунок?

Розв’язання

Нехай на перший рахунок вкладник поклав x грн, а на другий грн. Тоді разом він поклав у банк =12000 (грн). Відсотки, отримані за першим рахунком , складають 0,06x грн, а за другим рахунком 0,08y грн. За умовою, разом отримані  відсоткові гроші 0,06x+0,08y=800 (грн)

Маємо:     

Відповідь: 8000 грн, 4000 грн

Задача 3

Двоє робітників працюючи разом можуть виконати завадання, працюючи разом за 2 дні. За скільки днів може виконати це завдання кожний робітник, працюючи самостійно, якщо одному з них на виконання , менше, ніж іншому для виконання завдання

Розв’язання

Нехай перший робітник може виконати все завдання за x днів, а другий за y днів. Тоді за один день перший виконує а другий Оскільки за умовою вони виконують завдання за 2 дні, то разом вони виконують завдання отже, . Другий робітник виконує За умовою , Отримуємо систему

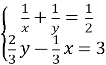
Звідси   

Відповідь: 3 дні, 6 днів

Задача 4 (самостійно)

З міста A в місто В, відстань між якими 320 км, виїхав вантажний автомобіль. Через 3 год після цього з міста В у місто А виїхав легковий автомобіль, який зустрівся з вантажним через  1 год після свого виїзду. Легковий автомобіль долає відстань між містами А і В на 1 год 20 хв швидше, ніж вантажний. Знайдіть швидкість кожного автомобіля.

Відповідь: 60 км/год і 80 км/год.

Домашнє завдання

Висновок: Сьогодні ми вивчили як застосовувати системи двох рівнянь до прикладних задач, розглянули задачі на рух, відсотки, спільну роботу.