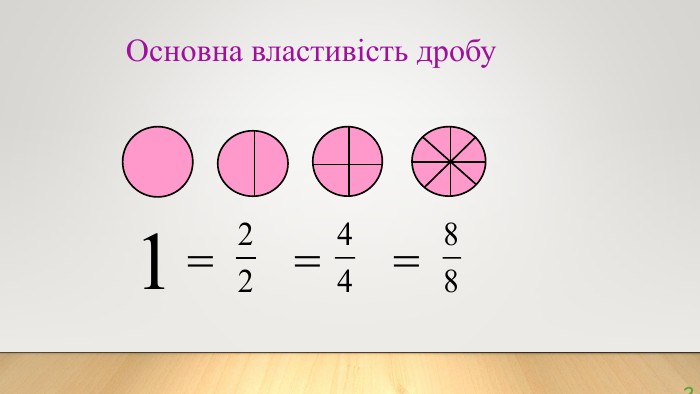
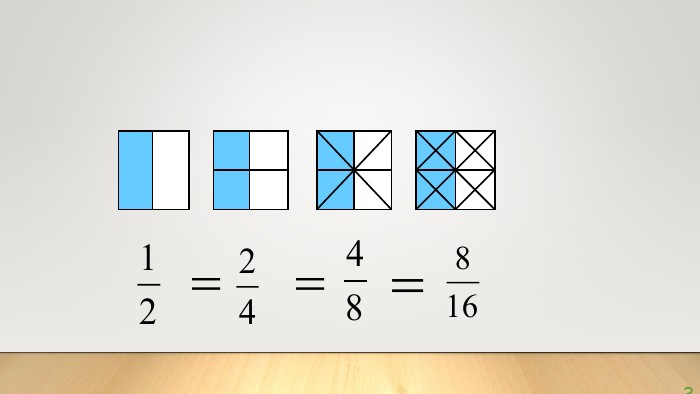
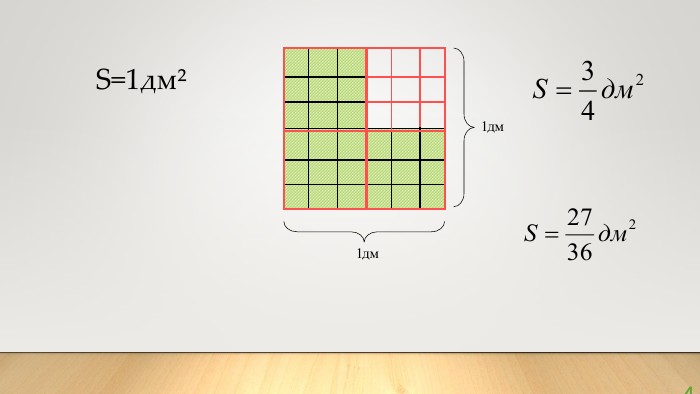
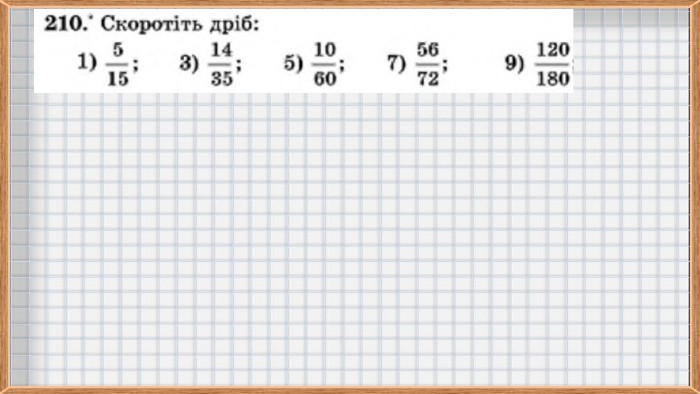
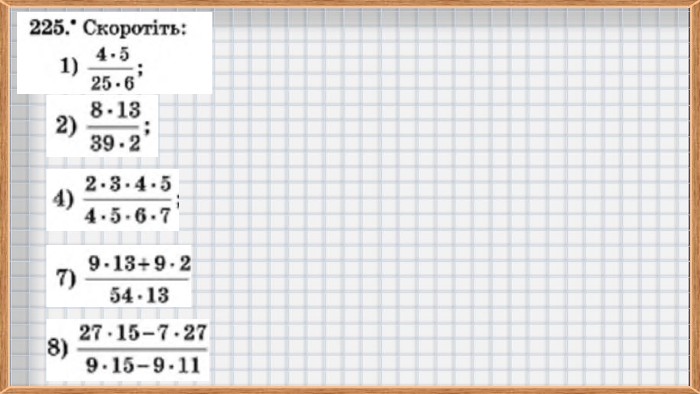
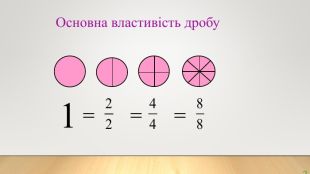
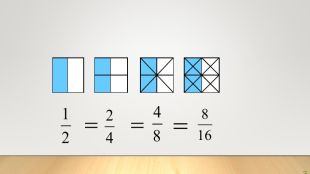
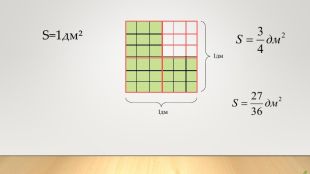
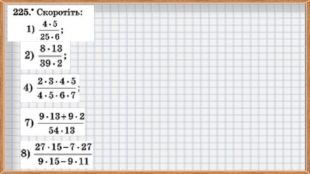
Скорочення дробів. Математика, 6 клас
Про матеріал
Презентація з теми: "Звичайні дроби. Скорочення дробів". Для вивчення звичайних дробів на математиці у 6 класі. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку