Стаття "Роль і місце практичних робіт на уроках математики у 5-6 класах в системі синергетичного мислення"

Роль і місце практичних робіт на уроках математики

у 5-6 класах в системі синергетичного мислення

Мало мати хороший розум,

 головне — 

                                                        добре його застосовувати.                                                                                                                                          Декарт

Однією з проблем сучасної методики викладання математики є реалізація зв'язку навчання з життям. Всім відомо, що знати і вміти не одне і те ж. Сам процес навчання, його процедура, спосіб взаємодії вчителя і учня з точки зору синергетики постає не як механічна передача знань від однієї до іншої людини, а створення умов, за яких стають можливими процеси народження знань самим учнем, його активна  і продуктивна творчість. Дана ситуація – це ситуація відкритого діалогу, прямого і зворотнього зв’язку, солідарної взаємодопомоги. Завдяки сумісній активності в такому контексті учитель і учень починають функціонувати в одному темпі. Для сучасної інноваційної освіти важливим є навчання, яке пробуджує. Проблема полягає в тому, як управляти, не управляючи, як малим резонансним впливом підштовхнути учня до саморозвитку, тобто до самоосвіти. В результаті синергетично осмисленого процесу освіти глибоко перебудовується особистість того, хто навчається. Навчання протікає як специфічна видозміна вже існуючих способів поведінки в напрямку того завдання, яке потрібно вирішувати. Завдання – це підготовка особистості учня до соціально-економічного життя, котра є складною синергетичною системою.

Проте до цих пір недостатньо приділяється уваги тому, щоб навчити учнів використовувати отримані знання на практиці. При вирішенні задач з задачника учень має справу тільки з поставленим і точно сформульованої проблемою. В реальному ж житті працівникові потрібно самому сформулювати задачу, самому визначити, від яких інших величин залежить значення шуканої величини, і самостійно знайти ці значення. Змінюється і характер освіченості людини. Час мислителів-універсалів відійшов в минуле. Сьогодні освіченість полягає не в об'ємі утримуваних в пам’яті знань з різних дисциплін, а в оволодінні загальною системою орієнтації в океані інформації, в створенні жорстких особистісних «фільтрів» чітких способів відбору цінної інформації. Тому в школі слід навчити учнів самостійно виділяти з реальних умов певні практичні проблеми і формулювати їх у вигляді математичних задач, а також самостійно визначати значення тих величин, від яких залежить відповідь на поставлене запитання.

Згідно з обласною програмою підвищення якості шкільної природничо-математичної освіти на період до 2015 року, потрібно створити умови для подальшого розвитку інтересу учнівської молоді до природничо-математичних наук. Математика - основоположна складова інших наук. Без математичних знань неможливо розвинути ніякі інші вміння: ні в інженерії, ні в космонавтиці, ні в медицині, ні в яких інших областях знань.

Застосування математичних знань на практиці, змінює відношення учнів до предмету, пробуджує інтерес до вивчення математики. Використання практичних робіт у викладанні математики допомагає вчителю зацікавити учнів, сформувати ситуацію успіху.

Дати дітям радість праці, радість успіху в навчанні, збудити в їхніх серцях почуття гордості, власної гідності - це перша заповідь виховання. У наших школах не повинно бути нещасливих дітей, душу яких гнітить думка, що вони ні на що не здібні. Успіх у навчанні – єдине джерело внутрішніх сил дитини, які породжують енергію для переборення труднощів, бажання вчитися.

Важливою умовою  удосконалення викладання математики - є посилення її практичної спрямованості. В. О. Сухомлинський наголошував, що виняткового значення слід надавати дослідницькому характеру розумової праці: спостерігаючи, думаючи, вивчаючи, зіставляючи діти знаходять істину або ж бачать, що для відкриття істини потрібні нові спостереження, потрібне читання, експериментування. Вироблення в учнів практичних умінь і навичок, формування життєдіяльнісних компетентностей - є один із шляхів розв’язання цієї проблеми.

Одними з форм організації дослідницької діяльності і є лабораторні та практичні роботи. При їх виконанні в учнів народжується істина, нове знання або розуміння математичних законів на практиці. Крім освітніх цілей лабораторні та практичні роботи відіграють роль в досягненні виховних і розвиваючих цілей. Важливо, щоб кожен учень розумів те, що він робить - цього можна досягти із застосуванням практичної діяльності, в якій школяр не тільки застосовує отримані знання, а й вчиться самостійно виконувати завдання, відповідальності за виконану роботу, засвоює окремі моменти досліджуваної теми.

Таким чином, використання лабораторних і практичних робіт при навчанні математиці допоможуть досягти наступних цілей:

• освітні: засвоєння математичних знань, формування практичних умінь і навичок, засвоєння принципів дії і навичок використання різних лічильних, вимірювальних і креслярських інструментів, вдосконалення знань учнів і навчання їх самостійному застосуванню цих знань, навчання вирішенню практико-орієнтованих завдань;

• виховні: формування акуратності та відповідальності за свою діяльність, активізація навчальної діяльності дослідницького характеру, формування умінь працювати в колективі;

• розвиваючі: розвиток спостережливості, вміння висувати і перевіряти гіпотези і припущення, спростовувати помилкові узагальнення і судження, розвиток інтересу до досліджуваного предмета.

Застосування лабораторних і практичних робіт, систематичне включення їх в навчальну роботу школярів для підвищення науково-теоретичного рівня, для посилення творчого характеру процесу навчання математики допомагає поліпшити якість математичних знань, є засобом формування міцних конструктивних, вимірювальних і обчислювальних умінь і навичок.

Практична робота - це діяльність учнів з роздатковим дидактичним матеріалом, вимірювання, ліплення, аплікація, малювання, моделювання тощо і використовується під час закріплення вмінь і формування навичок вимірювання, креслення, конструювання тощо. Як показують дослідження, для формування в учнів позитивного ставлення до навчання потрібне творення емоційно-сприятливої атмосфери на уроці, урахування життєвого досвіду школярів. Ці компоненти є складовою частиною роботи вчителів.

Це дає їм змогу на практиці використовувати діяльнісний метод навчання, при якому діти виступають у ролі активних шукачів інформації, дослідників, доповідачів, співрозмовників. Отримуючи мінімум готових фактів, діти виявляють максимум активного творчого пошуку. Саме така робота сприяє глибокому засвоєнню знань, розвитку пізнавальних інтересів, креативному збагаченню особистості.

Практичні роботи - є однією з активних форм навчання математики, які сприяють  розвитку і вихованню навичок і вмінь учнів , необхідних для застосування здобутих знань у практичних ситуаціях. Це такі форми  навчання, при яких учні самим безпосереднім чином включені в активний пізнавальний процес, в ході якого вони  визначають навчальну проблему; здійснюють збір необхідної інформації; планують шляхи розв’язання проблеми; роблять висновки;  аналізують свою діяльність ;  формують «по краплинці» нові знання, а головне - це одна із ефективних форм організації самостійної , пізнавально-пошукової діяльності учнів на уроці , де учні  набувають новий навчальний і життєвий досвід і тим самим знаходять відповідь  на запитання: «Навіщо мені потрібно вчити  математику?».

Під математичною практичною роботою (МПР) розуміють розв’язання деякої задачі з використанням певного обладнання: креслярських та вимірювальних інструментів, таблиць, графіків, допоміжних засобів обчислення (масштабна лінійка, штангенциркуль, калькулятор, комп’ютер). На практичних заняттях передбачають виготовлення моделей геометричних фігур (певної форми та розмірів), вимірювання довжин їх елементів, обчислення площ, об’ємів, величин кутів; знаходження площі, об’єму навколишніх об’єктів, зробивши попередньо необхідні вимірювання. Вимірювальні роботи на місцевості: знімання плану місцевості, знаходження недоступних відстаней тощо сприяють формуванню в учнів спостережливості за предметами певних геометричних форм у навколишньому середовищі (деталі, споруди), допомагають їм застосовувати набуті теоретичні знання до розв’язання завдань практичного змісту. При виконанні практичних робіт в деяких випадках учні «приходять» до важливих математичних відкриттів. Фактично аналіз знайдених результатів вимірювань приводить до думки про існування певного математичного твердження, а вже дедуктивні міркування стверджують істинність такого твердження.

Методика проведення практичних робіт з математики передбачає чітке визначення навчальної та виховної мети, інструктаж учнів щодо методики та послідовності їх проведення, забезпечення потрібних матеріальних засобів. Необхідно, щоб до кожної практичної роботи була коротка інструкція – інструкційна картка.

Суть практичних робіт полягає в застосуванні теоретичних знань під час розв’язання  практичних завдань, прикладних задач та створенні проектів. Також до  практичних робіт відносять ті самостійні роботи учнів, метою виконання яких є перевірка теоретично встановлених фактів, співвідношень, залежностей та застосування теоретичних знань на практиці.  Їх виконують після вивчення теми чи розділу курсу. За характером діяльності учнів  вони близькі до лабораторних робіт, сприяють поглибленню знань, навичок і вмінь, стимулюванню пізнавальної діяльності, дають змогу провести корекцію і контроль.

Під практичними роботами розуміють  такий вид пізнавальної діяльності з елементами навчального дослідження, який базується, перш за все, на виконанні навчальних завдань, для яких  характерно :

• завершений дослідницький цикл: спостереження - гіпотеза - перевірка гіпотези;
• використання  конструктивних методів із застосуванням безпосередніх вимірювань, побудов, зображень, геометричного моделювання та конструювання;
• спрямованість  на досягнення дидактичних цілей навчання.

Коли доцільно і методично виправдано на уроках математики проводити  практичні роботи ?

Аналіз навчальних програм із математики, алгебри , геометрії  підказує, що самостійну пізнавальну діяльність учнів засобом практичних робіт  варто проводити,  коли вчитель ставить учням завдання:

• виявити  істотні властивості математичних понять та встановити  зв'язки даного поняття з іншими;
• встановити закономірності та залежності між математичними величинами;
• узагальнити  та теоретично обґрунтувати  різні прикладні задачі;
• створити модель геометричної  фігури  чи   ситуації;
• скласти  нові задачі , що випливають з розв’язання даних;
• застосувати теоретичні знання до розв’язування практичних завдань, прикладних задач.

Готуючись до практичної роботи, вчитель підбирає такі завдання, які забезпечать формування компетенцій учнів у самостійній пізнавальній діяльності.  Тому постановка запитання в задачі повинна бути такою, що тільки,  коли  учень проведе   дослідження, то зможе знайти на нього  відповідь;  умова задачі має забезпечувати  використання різних методів і способів розв’язання;  в умовах завдань повинні бути відсутні прямі вказівки на використання відомих теорем і формул та шляхів розв’язання поставленої проблеми.

До практичних робіт учитель вдається перед поясненням нового матеріалу (для актуалізації опорних знань та умінь), у процесі розповіді (для ілюстрування теоретичних положень) або після вивчення матеріалу (з метою узагальнення і систематизації комплексного застосування знань).

Перші практичні роботи у 5 класі бажано проводити тільки в класі. Вони повинні бути нетривалими. Їх необхідно виконувати разом з учнями, використовуючи плакати, переносні дошки, тощо. Про проведення практичних робіт учнів потрібно повідомляти заздалегідь. Учитель повинен пояснити, скільки часу дається на виконання роботи, які вимоги пред'являються до оформлення роботи.

Вимоги щодо виконання практичних завдань змінюються із зміною віку учнів і їх математичного розвитку. Якщо, наприклад, у 5 класі цілком досить виконати вимірювання і зробити відповідні обчислення, то в 7 і 8 класах, крім потрібних вимірювань і обчислень, учні повинні зробити певні обґрунтування, чому саме так треба виконувати завдання.

Під час виконання роботи учні записують у зошитах тему, мету та хід роботи. Практичні роботи оформляються в робочих зошитах. Науковці-методисти В.І. Мокін, В.О. Папьєв, О.В. Мокін пропонують використовувати такі різновиди практичних робіт як:

1. Ознайомчі практичні роботи, що передбачають формування вмінь і навичок користування приладами, пристроями, необхідних для виконання завдань.

2. Підтверджуючі практичні роботи, виконання яких має на меті підтвердження правильності отриманих теоретичних знань.

3. Частково-пошукові практичні заняття, що стимулюють самостійність та творче мислення учнів. В інструкціях до таких робіт вказується тема, мета, завдання, загальний план досліджень та орієнтований перелік запитань, на які слід знайти відповіді. Учні самостійно деталізують план дослідження і вибирають траєкторію руху для досягнення мети дослідження.

4. Дослідні практичні роботи мають лише мету дослідження, усі інші етапи роботи учні планують самостійно. Такий вид робіт вимагає великих часових затрат, високої інтелектуальної напруги і передбачає відповідне оцінювання.

Практичні роботи можуть бути організовані як у класі, так і задані додому. Залежно від обсягу та змісту матеріалу, можуть бути організовані на цілий урок, на частину уроку або задані у вигляді домашнього завдання.

Готуючись до уроку,  визначаю такі етапи проведення  практичних робіт:

•         Повідомлення теми і мети роботи; повторення теоретичного матеріалу, потрібного для виконання роботи.
•         Ознайомлення зі змістом та описом роботи, яку слід виконати; здійснення необхідного інструктажу щодо етапів роботи, послідовності виконання вимірювань та обчислень, схеми оформлення роботи.
•         Самостійне виконання кожним учнем роботи, запис результатів вимірювання та обчислень до таблиці.
•         Спостереження вчителя за роботою учнів, перевірка правильності вимірювань та обчислень.
•         Підбиття підсумків виконання роботи.

Під час оцінювання якості виконання роботи враховую правильність побудов і обчислень, раціональність, уміння виконувати наближені обчислення, а також, охайність роботи. Оцінки за окремі практичні заняття враховую, виставляючи тематичну оцінку.

Програмою шкільного курсу математики проведення практичних робіт не передбачено. Але не варто недооцінювати роботи такого виду. Проводити їх на кожному уроці необов’язково,але користуючись ними,можна розвинути в учнів потребу експериментувати під час розв’язування різних математичних задач. Вони дозволяють учням повніше і свідоміше усвідомити математичні залежності між величинами, ознайомитися з вимірювальними математичними приладами та їх застосуванням на практиці, навчитися вимірювати і обчислювати з певним ступенем точності, використовувати ІКТ, що забезпечує високу ефективність та результативність.

Роблячи підсумок з усього викладеного, можна сказати, що практичні роботи на уроках математики :

• Розвивають творче мислення школярів;
• Дають можливість охопити і зацікавити всіх учнів класу;
• Підвищують активність і самостійність учнів на уроці;
• Сприяють розвитку допитливості, кмітливості, почуття відповідальності;
• Після проведення роботи її суть краще закарбовується в пам’яті;
• У учнів народжується розуміння  математичних законів на практиці та чітке переконання, що «математика - безмежна і різноманітна як світ, присутня  і міститься в усьому» (М.П. Яругін)…

Література:

1. Кремень В. Г.  Освіта і суспільство в парадигмі синергетичного мислення. Педагогіка і психологія. Вісник НАПН України
2. Пометун О. І., Пироженко Л. В. Сучасний урок. Інтерактивні технології навчання: Науково-методичний посібник. К.: А. С. К., 2003.
3. Раков С.А. Математична освіта: компетентнісний підхід з використанням ІКТ: Монографія. – Х.:Факт, 2005. – 360с.
4. Реп'єв, В.В. Загальна методика викладання математики.
5. Сухомлинський В. О.. Сто порад учителеві. — К.,1982.
6. Шарко В. Д. Сучасний урок // К.: 2006, 224 с.

Розробки практичних робіт з математики для 6 класу.

Практична робота № 1

Тема: Дослідження ознак подільності та практичне їх застосування.

Мета: закріпити ознаки подільності на 2, 5, 10, 9, 3. Навчитися розв’язувати задачі з даної теми. Закріпити вміння знаходити НСД та НСК і з’ясувати практичну необхідність вивчення теми «Ознаки подібності» в шкільному курсі. Розвиток інтересу до досліджуваного предмета.

Обладнання: олівець, лінійка, ручка, картки з завданнями, рулетка, цукерки, комп’ютер.

Хід роботи

ІV. Практична робота  (робота в групах)

Картку з завданням отримує кожна група.(правила роботи у групі на дошці)

1. Ось перед кожним з вас лежить стрічка. Яку найменшу довжину вона повинна мати, щоб її можна без обрізків розділити на частини завдовжки як 30 см, так і 75 см?
2. Перед вами є цукерки двох видів. 10 цукерок одного виду. 15 – другого. По скільки цукерок різного виду отримає кожен учень вашої групи?
3. Загадкове число. У єгипетській піраміди на гробниці накреслено число 2520. Чому саме для цього числа випала «така честь»? (Вказівка. Це число ділиться на всі натуральні числа від 1 до 10. Перевірте це).

Аналіз експериментів та їх результативність

1. Представник групи перевіряє результати роботи на «Онлайн калькуляторі»
2. Інші учні аналізують результати своєї роботи та дають відповіді на такі запитання: Метод евристичних запитань за Квінтіліаном: Що? Хто? Коли? Навіщо? Де? Чим? Як?

1. Що? Що за тему ми сьогодні закріпили?
2. Хто? Хто з вчених працював над вивченням ознак подільності?
3. Коли? Коли ще вміли знаходити НСК та НСД?
4. Навіщо? Для чого нам потрібні дані знання?
5. Де? В яких галузях застосовуються дані знання?
6. Чим? Чим цікавим ви зможете зайнятися вміючи знаходити НСД та НСК натуральних чисел?
7. Як? Як дані знання можна застосувати в житті?

V. Оцінювання практичної роботи.

Самооцінювання (правильні відповіді завдань проектуються на екран)

VІ. Доповідь учня. Знаходження НСД за алгоритмом Евкліда.

VІІ. Рефлексія.

VІІІ. Домашнє завдання.

Підготувати по дві задачі з даної теми.

                              Практична робота № 2

Тема: Масштаб. Робота з картою.

Мета: Закріпити вміння знаходити відстань на карті, вміння складати план кімнати, будинку. Активізація навчальної діяльності дослідницького характеру, розвиток інтересу до досліджуваного предмета. З’ясувати практичну необхідність вивчення теми «Масштаб» в 6 класі.

Обладнання: карта України, лінійка, ручка, олівець, рулетка.

ХІД РОБОТИ

ІІ. Розминка.

1. Виміряй за картою відстань між містами:

Київ – Харків;

Київ – Одеса;

Херсон  – Київ;

Київ – Берислав

Знайди відстань між цими містами, якщо масштаб 1:10 000 000

 (в 1 см 100 000 м)

ІІІ. Застосовуємо на практиці

1. Довжина автомобільної дороги Львів – Київ наближено дорівнює 530 км. Зобрази відрізком автомобільну дорогу в зошиті, узявши за масштаб 1:7000000.

      ІV. Задачі краєзнавчого характеру по Херсонській області

  Користуючись запропонованою Вам картою, з масштабом 1 : 1 000 000 

 знайдіть відстань між:

                    - містами Бериславом та Херсоном;

• містами Бериславом та Новою Каховкою;
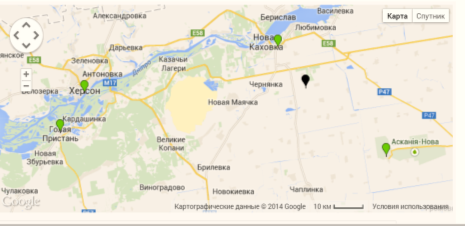• містами Бериславом та Асканією –Новою.

1. Відстань від м.Берислав до с. Тягинка  33 км. а на карті – 11 см. Знайдіть масштаб карти.
2. Довжина автомобільної дороги Берислав – Аскания Нова наближено дорівнює 105км. Зобрази відрізком автомобільну дорогу в зошиті, узявши за масштаб 1:2000000.
3. Довжина Арбатської стрілки  на місцевості 115 км. Яка буде довжина  півострову на карті з масштабом 1 : 200 000.

VІІІ. Домашнє завдання.

1. Скласти план вашої кімнати в зошиті.

Практична    робота   №3

Тема. Пропорція

Мета :формувати   вміння   розв’язувати  задачі із  застосуванням   пропорцій;

•  формування  пошуково -  смислового  поля, вміння  працювати  

 групами;

•  виховувати  свідоме  ставлення  до  своєї  діяльності,  прагнення   до  

 досконалості.

ХІД РОБОТИ

І. Організаційний момент.

    ІІ. Розминка.

1.                    Заміни  зірочки  так, щоб  отримати  правильні  пропорції

6 : * = 36 : 30;                                      */5 = 21/15

3. На  пошиття  14  костюмів  витратили  49 м  тканини. Скільки  таких  самих   костюмів  можна  пошити  з  84  м  цієї  тканини ?

ІІІ.  Застосовуємо на практиці

Задача. З  20 кг морської води можна  добути  0,5 кг солі. Скільки  потрібно  взяти  морської  води, щоб  отримати  45 кг солі?

Задача. З  10 кг  жита  виходить 9 кг   борошна  . Скільки  треба  змолотити  жита  щоб отримати 900 кг борошна ?

ІV. Осмислення  і  оцінка  власного  рівня  навченості .

    Кожен  учень  аналізує  свою  активність  і  впевненість  на  уроці. Підраховуються  набрані  бали  в  ході  розв’язування  задач.

V. Підсумок  уроку  здійснити  з  використанням    карток  зворотного  зв’язку « так» , « ні»

• Чи  зрозуміла  вивчена  тема?
• Чи відчував  втому  на  уроці?
• Чи  переконався  в  необхідності   теми « пропорції»  при  розв’язуванні  практичних  задач ?
• Чи  залишився  задоволений  собою?

 Практична робота № 5

Тема: Довжина кола й площа круга.

Мета: Навчитися визначати радіус, діаметр, хорду кола. Будувати кола з заданим радіусом та діаметром. Обчислювати діаметр та радіус побудованих кіл. Вчитися знаходити довжину кола та площу круга в задачах пов’язаних з повсякденним життям.

Обладнання: циркуль, олівець, лінійка, чернетка, кольорові олівці,  ножиці, нитки, циркуль, клей, калькулятор, картон, кольоровий папір

 ІV. Практична робота.

1. Учні в  парах виконують практичні завдання по інструкції й записують свої спостереження:

1) На картонному аркуші накреслити кола довільного радіуса, відзначити її центр, записати значення радіуса в міліметрах (R) і значення діаметра в міліметрах(D).

2) Провести клеєм-олівцем по колу  й, поки клей не висохнув, прокласти нитку точно по контуру кола й акуратно відрізати її на стику.

3) Зняти нитку з картону й дуже точно виміряти її довжину в міліметрах. Цей розмір назвемо довжиною окружності (L). Записати значення L.

4) Знайти відношення    за допомогою калькулятора, округлити  дріб, що вийшов, до тисячних,  до сотих, до десятих, до цілих. Зробити відповідні записи.

5) Занести всі результати в таблицю:

4. Учні в парах виконують практичні завдання по наступній інструкції:

1)      На аркуші кольорового паперу накреслити коло довільного радіуса й провести фломастером по її контурі.

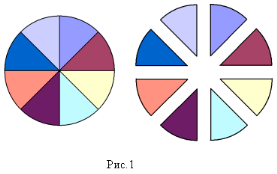2) Розділити коло за допомогою лінійки й олівця на кілька  секторів, потім розрізати його (див. мал.1).  Коло варто розділити як мінімум на 8 секторів.

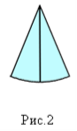3) В одному із секторів варто провести радіус, що ділить його на 2 рівні сектори, які назвемо крайніми (див. мал.2) і відкласти його.

 4) На картонному аркуші провести горизонтальну пряму й приклеїти уздовж її сектори, як показано на мал.3. Крайні сектори приклеїти по краях.