STEM у освітньому процесі школи .Проект «Многранники та кристали»

УКРАЇНА

ДЕПАРТАМЕНТ ОСВІТИ ТА ГУМАНІТАРНОЇ ПОЛІТИКИ

КОМУНАЛЬНА УСТАНОВА «ЧЕРКАСЬКИЙ МІСЬКИЙ МЕТОДИЧНИЙ КАБІНЕТ УСТАНОВ ОСВІТИ»

ЧЕРКАСЬКОЇ МІСЬКОЇ РАДИ

ЧЕРКАСЬКА СПЕЦІАЛІЗОВАНА ШКОЛА І – ІІІ СТУПЕНІВ № 28

імені Т.Г. ШЕВЧЕНКА

ЧЕРКАСЬКОЇ МІСЬКОЇ РАДИ ЧЕРКАСЬКОЇ ОБЛАСТІ

 

 

 

 

 

 

 

 

 

Леонова В.Л

 

 

STEM у освітньому  процесі  школи

 

 

 

 

 

 

 

 

Черкаси – 2020

 

 

 

STEM у освітньому процесі школи

 

Упорядник матеріалів: Леонова Валентина Леонтіївна  – вчитель математики Черкаської спеціалізованої школи І - ІІІ ступенів №28 імені

Т.Г. Шевченка Черкаської міської ради Черкаської області

 

 

 

 

Збірка матеріалів містить роботи із упровадження елементів STEM-освіти в навчанні математики, хімії, географії, інтеграції навчальних предметів, забезпечення тісного взаємозв’язку суміжних наук у процесі навчання.

Представлені матеріали роботи вчителів у навчальних проектах, що сприяють  створенню умов щодо збалансованого гармонійного формування науково-орієнтованої освіти на основі модернізації математично-природничого та гуманітарних профілів освіти.

 Матеріали можуть бути використані вчителями математики, георафії та хімії при вивченні відповідних тем на уроках та для проведення позакласних заходів

 

 

 

 

 

 

 

Схвалено педагогічною радою Черкаської спеціалізованої школи

І – ІІІ ступенів № 28 ім. Т.Г. Шевченка Черкаської міської ради Черкаської області

 Протокол № 4 від 05 березня 2020 року

 

 

 

 

Проект «Многранники  та  кристали»

Девіз проекту:

   Найвище призначення  математики полягає в тому, щоб знаходити прихований порядок в хаосі, що оточує нас 

Н. Вінер

 Місце проведення: Черкаська спеціалізована школа І – ІІІ ступенів № 28 імені Т.Г. Шевченка Черкаської міськогї ради Черкаської області

Предмет:  Хімія, математика

Вік учнів: 10- 14 років

Склад учасників проекту: учні, вчитель математики Леонова Валентина Леотіївна, Шепета оксана Миколаівна хімії, Ковальова Марина Юріївна

Тип проекту: Пізнавальний, дослідницький, творчий

За кількістю учасників: груповий

За тривалістю підготовки: короткотривалий ( два тижні)

Актуальність теми:

Вирощування кристалів в домашніх умовах – дуже захоплююче заняття. Його можна віднести до виготовлення виробів з природного матеріалу, тому що необхідна для цього сіль - матеріал натуральний, природний.Крім цього, експерименти з вирощуванням кристалів прості, доступні, недорогі і відносно безпечні, завдяки чому зайнятися цією цікавою справою може кожен. Зможете відточити свої навички лабораторної роботи, поводження з речовинами, організації плану роботи і т. д.

Освітня:

• Поглибити знання учнів про правильні многогранники;
• Показати значення правильних многогранників з історичної і
• математичної точки зору;
• навчитися експериментувати з різними солями, спробувати підфарбовувати розчин, робити його більш-менш насиченим, швидше або повільніше остуджувати;спостерігати за розмірами і формою кристалів;
• розвивати  вміння отримувати інформацію з різних джерел.
• Показати взаємозв’язок вивчених на уроці тем з навколишнім

світом і оточуючим нас побутом.

Розвиваюча:

• Розвивати пізнавальний інтерес до математики;

• Розвивати художнє бачення, навички режисури;

• Сприяти вихованню активного мислення, комунікативних

якостей учнів;

Виховна:

• Виховувати творче мислення, всебічно розвинуту особистість;

• Виховувати естетичний смак, уміння цінувати прекрасне;

Завдання проекту:

• дослідити«присутність»правильних многогранників в природі та побуті;
• довести необхідність вивчення  геометрії для практичного застосування  у житті;
• виростити кристали мідного купоросу та натрій хлориду;
• опрацювати літературні джерела та ознайомитись з будовою, властивостями та застосуванням кристалів;
• спостерігати за розмірами та формою вирощених кристалів
• викликати  бажання провести дослідження та дізнатися більше про кристали, їх будову, застосування у різних сферах життя  людини,навчитися вирощувати кристали в домашніх умовах, спостерігаючи за зміною їх форми
• викликати  бажання провести дослідження та дізнатися більше про кристали, їх будову, застосування у різних сферах життя  людини,навчитися вирощувати кристали в домашніх умовах, спостерігаючи за зміною їх форми
• •підготувати експозицію творчих робіт учнів;
• •зробити  презентацію та провести захист  проекту.

Очікувані результати

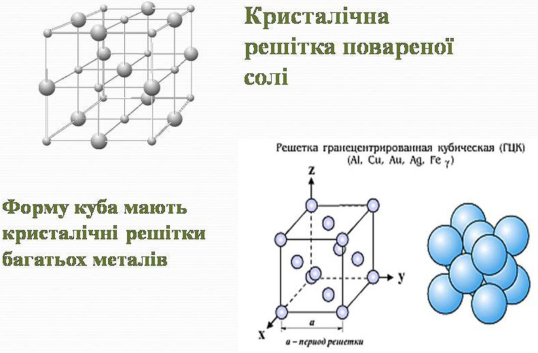
•  освоєні знання про насичені розчини, вплив температури на розчинність речовин, властивості кристалів, вузли, кристалічні решітки, внутрішню будову кристалів, методи їх вирощування, застосування, приклади росту кристалів у природі.
• Покращення   навиків роботи з речовинами, мережею Інтернет, довідковою літературою;
• Підвищення  рівня  співпраці між учнями;
• Отримання учнями позитивних балів за завдання та задоволення  від виконаної роботи.

     Мотивація

Є в шкільній геометрії особливі теми, які чекаєш з нетерпінням, передчуваючи зустріч з неймовірно красивим матеріалом. До таких тем можна віднести тему "Правильні многогранники". Тут не тільки відкривається дивовижний світ геометричних тіл, що володіють неповторними властивостями, але і цікаві наукові гіпотези. Ні одні геометричні тіла не володіють такою досконалістю і красою, як правильні многогранники. Сьогодні    ми дізнаємося і побачимо багато цікавого, нам належить відповісти на такі питання, як, наприклад: Які многогранники  називаються  правильними? Скільки їх існує? Що таке Ейлерова характеристика? Які тіла носять назву тіл Кеплера - Пуансо? І багато – багато інших... І, нарешті: де, навіщо і для чого нам потрібні многогранники? Можливо, в житті можна обійтися і без них? Даний  проект стане в нагоді нам при вивченні теми “Об’єми многогранників» і при розв’язуванні задач на комбінації геометричних тіл.

І Підготовчий етап

«Скажи  мені–і я забуду,

Покажи  мені–і я запам’ятаю,

дай  зробити–і я зрозумію»

Історики –вивчають значення правильних многогранників з історичної і математичної точки зору

Теоретики-дослідники–вивчають матеріал з підручника та додаткових джерел та досліджують застосування многогранників в природі та архітектурі

Практики –виготовляють моделі  правильних многогранників для наочності

ІІ Відбір матеріалу

Правильні многогранники

Правильним многогранником є многогранник, грані якого є правильними многокутниками з рівною кількістю сторін, а в кожній вершині многогранника сходиться однакова кількість ребер.

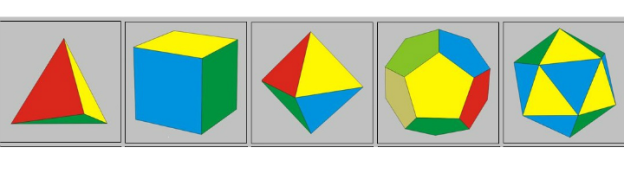
Існує п’ять типів правильних опуклих многокутників: правильний тетраедр, куб, октаедр, додекаедр, ікосаедр.

У правильного многогранника:

- усі ребра рівні;

- усі двогранні кути, що містять дві грані зі спільним ребром, також рівні;

У правильного тетраедра всі чотири грані – рівносторонні трикутники. Кожна з його вершин є вершиною трьох трикутників. Сума плоских кутів при кожній із вершин дорівнює 180 градусам. Правильний тетраедр не має центра симетрії.

У правильного октаедра всі вісім граней – рівносторонні трикутники. Кожна вершина октаедра є вершиною чотирьох трикутників. Сума кутів плоских кутів при кожній вершині дорівнює двомстам сорока градусам. Правильний октаедр має центр симетрії.

У правильного ікосаедра всі двадцять граней – рівносторонні трикутники. Кожна з вершин ікосаедра є вершиною п’яти трикутників. Сума плоских кутів при кожній з вершин ікосаедра дорівнює трьомстам градусам. Правильний ікосаедр має центр симетрії.

У куба всі шість граней – квадрати. Кожна з вершин куба є вершиною трьох квадратів. Сума плоских кутів при кожній з вершин куба дорівнює двомстам сімдесяти градусам. Куб має один центр симетрії.

У правильного додекаедра всі дванадцять граней – правильні п’ятикутники. Кожна з вершин додекаедра є вершиною трьох правильних п’ятикутників. Сума плоских кутів при кожній з вершин дорівнює трьомстам двадцяти чотирьом градусам. Правильний додекаедр має центр симетрії.

Інших видів правильних многогранників не існує. Не існує правильного многогранника, гранями якого є правильні шестикутники, семикутники і взагалі n-кутники з кількістю сторін, більшою за п’ять.

 

Історія

          Усі правильні многогранники були відомі ще в Стародавній Греції, і їм еприсвячена заключна, 13-я книга відомих “Начал” Евкліда. Як говорилося раніше, ці многогранники часто називають також платоновыми тілами - в ідеалістичній картині світу, даній великим давньогрецьким мислителем Платоном, чотири з них уособлювали 4 стихії: тетраедр - вогонь, куб - землю, ікосаедр - воду, октаедр - повітря, п'ятий же многогранник, додекаедр, символізував весь всесвіт - його по-латині стали називати quintaessentia (квінта есенція), що означає все найголовніше, основне, сутність чого-небудь.

Правильні многогранники іноді називають Платоновими тілами, оскільки вони займають чільне місце у філософській картині світу, розробленій великим мислителем Стародавньої Греції Платоном (ок. 428 - ок. 348 до н.е.).

Платон вважав, що світ будується з чотирьох «стихій» - вогню, землі, повітря і води, а атоми цих «стихій» мають форму чотирьох правильних многогранників. Тетраедр уособлював вогонь, оскільки  його вершина спрямована вгору, як у полум'я, що розгорілося; ікосаедр - як обтічний - воду; куб - найстійкіша з фігур - землю, а октаедр - повітря. У наш час цю систему можна порівняти з чотирма станами речовини - твердим, рідким, газоподібним і полум'яним. П'ятий многогранник – додекаедр символізував весь світ і вважався айголовнішим.

              Це була одна з перших спроб ввести в науку ідею систематизації.

Вчитель: А тепер від Стародавньої Греції перейдемо до Європи XVI - XVII ст., коли жив і творив чудовий німецький астроном, математик Йоганн Кеплер (1571 - 1630).

Уявімо себе на місці Кеплера. Перед ним різні таблиці, стовпчики цифр. Це результати спостережень руху планет Сонячної системи - як своїхвласних, так і великих попередників - астрономів. У цьому світі обчислювальної роботи він хоче знайти деякі закономірності. Йоганн Кеплер, для  якого правильні многогранники були улюбленим предметом вивчення, припустив, що існує зв'язок між п'ятьма правильними многогранниками і шістьма відкритими до того часу планетами Сонячної системи. Згідно з цим припущенням, в сферу орбіти Сатурна можна вписати куб, в який вписується сфера орбіти Юпітера. В неї, в свою чергу, вписується тетраедр, описаний навколо сфери орбіти Марса. У сферу орбіти  Марса вписується додекаедр, в який вписується сфера орбіти Землі. А вона описана навколо ікосаедра, в який вписана сфера орбіти Венери. Сфера цієї планети описана навколо октаедра, в який вписується сфера Меркурія. Така модель Сонячної системи отримала назву «Космічного кубка» Кеплера. Результати своїх обчислень вчений опублікував у книзі «Таємниця всесвіту». Він вважав, що таємниця Всесвіту розкрита. Рік за роком вчений уточнював свої спостереження, перевіряв дані колег, але, нарешті, знайшов у собі сили відмовитися від привабливої гіпотези. Однак її сліди проглядаються в третьому законі Кеплера, де говориться про куби їх середніх відстаней від Сонця.

            Сьогодні можна з упевненістю стверджувати, що відстані між планетами і їх кількість ніяк не пов'язані з многогранниками. Звичайно, структура Сонячної системи не є випадковою, але справжні причини, за якими вона влаштована так, а не інакше, до цих пір не відомі. Ідеї Кеплера виявилися помилковими, але без гіпотез, іноді найнесподіваніших, здавалося б, маревних, не може існувати наука.

           Ідеї  Платона і Кеплера про зв'язок правильних многогранників з гармонійним устроєм світу і в наш час знайшли своє продовження в цікавій науковій гіпотезі, яку на початку 80-х рр. висловили московські інженери Ст. Макаров і Ст. Морозов.  Вонив важають, що ядро Землі має форму і властивості зростаючого кристала, що впливає на розвиток всіх природних процесів, що відбуваються на планеті. Промені цього кристала, а точніше, його силове поле, обумовлюють ікосаедро-додекаедрову  структуру  Землі Вона проявляється в тому, що в земній корі немов би проступають проекціїв писаних в земну кулю правильних многогранників: ікосаедра і додекаедр.

             Багато покладів корисних копалин тягнуться вздовж ікосаедро-додекаедрової сітки; 62 вершини і середини ребер многогранників, які звуться авторами вузлами, володіють рядом специфічних властивостей, що дозволяє пояснити деякі незрозумілі явища. Тут розташовуються осередки найдавніших культур і цивілізацій: Перу, Північна Монголія, Гаїті, Обська культура та інші. В цих точках спостерігаються максимуми і мінімуми атмосферного тиску, гігантські завихрення Світового океану. В цихв узлах знаходяться озеро Лох-Несс, Бермудський трикутник. Подальші дослідження, можливо, визначать ставлення до цієї наукової гіпотези, в якій, як видно, правильні многогранники займають важливе місце.

Леонард Ейлер

 

Відомий  швейцарський  математик

відкрив і довів знамениту формулу В –Р + Г = 2.

Що зв’язує числа вершин, ребер і граней будь-якого опуклого многогранника.

 

                      Луї Керролл писав:

"Правильних многогранників надзвичайно мало, але цей досить скромний за чисельністю загін зумів пробратися в самі глибини різних наук".

 

 

 У глибини яких наук пробралися правильні многогранники? Де в житті ми можемо їх зустріти?

Многогранники в архітектурі

Будинок у Словаччині: на з’єднанихміж собою тумбах стоять на ребрах кубики. Кожен кубик –триярусна квартира

Білоруська

національна

бібліотека

 

 

 

 

 

Пам’ятник  

Футбольному мячу

 в Харкові

 

Правильні  многогранники в природі

"Математика володіє не лише істиною, але і вищою красою -красою  вигостреної і строгої, піднесено чистої прагнучої до  справжньої досконалості, яка властива лише найбільшим зразкам мистецтва"

Бертран Рассел.

 

Тетраедр в природі

 

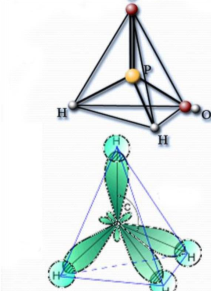
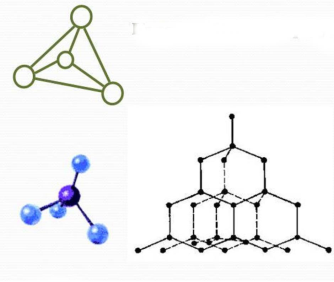
                 Кристалічна решітка метану

5. Практична робота

Робота в групах. Об’єднатися в групи, обрати назву (“Додекаедр, Тетраедр, Октаедр)

Отримати теми дослідження.

Завдання команді «Додекаедр»:

Підготувати інформацію про кристали

• Загальна характеристика, класифікація
• https://uk.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB
• Кристалічні гратки
• Дефекти кристалічних решіток
• http://bibliograph.com.ua/spravochnik-104-stroymaterialy/8.htm
• Рідкі кристали та їх використання
• https://uk.wikipedia.org/wiki/%D0%A0%D1%96%D0%B4%D0%BA%D1%96_%D0%BA%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D0%B8
• https://www.youtube.com/watch?v=UuSmVAGroVE
• https://pan-gospodar.com.ua/vyrashhivanie/yak-viroschuvati-shtuchn-kristali-v-domashn-h-umovah.html
• Кристали вирощені для наукових цілей
• http://bibliograph.com.ua/spravochnik-50/48.htm
• Вирощування кристалів в домашніх умовах
• https://www.youtube.com/watch?v=IM6tBi6OIXY
• https://www.youtube.com/watch?v=-Q5EFuzreyY
• https://www.youtube.com/watch?v=cgeCHNyosg4

Завдання команді «Октаедр»

Підготувати інформацію про кристали в географії

• Український кристалічний щит
• https://uk.wikipedia.org/wiki/%D0%A3%D0%BA%D1%80%D0%B0%D1%97%D0%BD%D1%81%D1%8C%D0%BA%D0%B8%D0%B9_%D0%BA%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D1%96%D1%87%D0%BD%D0%B8%D0%B9_%D1%89%D0%B8%D1%82
• Кристалічні породи
• https://uk.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D1%96%D1%87%D0%BD%D1%96_%D0%BF%D0%BE%D1%80%D0%BE%D0%B4%D0%B8

           Коли дитина вже подорослішала, разом з гордістю приходить і усвідомлення того, що його все складніше чимось зацікавити, здивувати і всерйоз захопити. Є, однак, спосіб, про який багато хто забуває, але таке проведення часу запам'ятається на все життя. «Що ж це за гра?» - запитає читач. Нічого складного і витратного, просто покажіть дитині, що таке правильний многогранник і він його побудує його модель , покажіть, як  і він , з великим задоволенням, займеться   вирощуванням кристалів. Для дітей цей урок стане колосальним відкриттям.

Що таке кристал?

Відповідь на це питання проста у книжковому варіанті: це впорядкований будова твердого речовини. Начебто нічого складного, але набагато простіше зрозуміти поява цього дива природи на власному досвіді. Хоча насправді ми щозими бачимо вирощування кристалів. Для дітей немає нічого цікавіше того, як з'являються сніжинки і гарний візерунок на вікні. А насправді це все теж кристали! Вони проявляються при поступовому зниженні температури води, частинки вологи притягуються і утворюють прекрасні кристалики. Пораздумав, дитина неодмінно зацікавиться тим, де він ще може побачити подібне явище. На допомогу тоді прийдуть сіль і цукор. Їх маленькі крихти – це теж кристали. І мамина дорогоцінна шкатулка, на якій є різні камені. Неважливо, штучні стрази або натуральні дорогоцінні мінерали. Саме вони допоможуть показати дитині все досконалість ліній, а також надихнуть створити таку красу. Тим більше що обладнання для вирощування кристалів є в кожному будинку, а реагенти – на кухні.

             Розгортки, які утворяться, необхідно роздрукувати  учням для виконання домашнього завдання.

1 група - довести, що правильних многогранників 5.

2 група – заповнити таблиці і зробити висновок.(моделі).

3 група – вивести формули повної поверхні правильних многогранників.

4-5 групи – виростити  кристали, та продемострувати  їх.

ІІІ етап(практичне завдання)

Побудова моделей правильних многогранників:

Правильні многогранники - найвигідніші фігури. І природа цим широко користується. Багато властивостей кристалів, які вивчаються  на уроках фізики і хімії, пояснюються їх геометричною будовою. Тому властивості багатогранників  використовуються і в кристалографії. Бджоли будували шестикутні стільники задовго до появи людини, а в історії цивілізації створення багатогранних тіл (подібних до пірамід) разом з іншими видами пластичних мистецтв йде углиб віків.                      

Творча робота юних математиків( Керівник Леонова В.Л)

http://qrcoder.ru/code/?https%3A%2F%2Fsites.google.com%2Fsite%2Fpaperovijsvitorigami%2Ffiguri%2Ftransformeri&4&0

ТТв

 

 

 

 

 

Вирощування кристалів кухонної солі

Процес вирощування кристалів кухонної солі не вимагає яких-небудь особливих реагентів. Розчин готується так: в ємність наливається вода, і ємність ставиться в каструльку з теплою водою (не гаряче 60 градусів). У ємність насипте сіль і залиште хвилин на п’ять, заздалегідь розмішавши. Ємність нагріється, і тоді сіль розчиниться (слідкуйте, щоб температура води не знижувалася). Додайте ще солі і ще раз перемішайте, поки сіль не припинить розчинення і не почне осідати на дні. Насичений розчин готовий – перелийте його в чисту ємність аналогічного обсягу, прибравши надлишки солі на дні. Тепер візьміть будь-який більш-менш великий кришталик кухонної солі, перетворіть його на нитку і підвісити, щоб він не торкався стінок ємності, або просто покладіть на дно. Тепер залишається тільки чекати – вже через пару днів ви можете помітити значне збільшення кришталика, і він буде рости кожен день. Щоб швидше виростити кристал, додайте в розчин сіль, щоб він завжди був насиченим. У ста грамах води при 20 градусах розчиняється близько 35 грамів кухонної солі.

Виготовлення кристалів мідного купоросу

Такі кристали можна виростити аналогічним чином готується насичений розчин, і в нього опускається невеликий кристалик мідного купоросу. Пам’ятайте, що мідний купорос – активна речовина, і буде краще використовувати дистильовану воду. Та, що з під крана може містити сполуки, які вступають в реакцію з мідним купоросом і зіпсують розчин. Насичений розчин перелити в іншу ємність, підвішуємо так, щоб він був повністю покритий розчином і не торкався стінок посудини, потім залишається тільки чекати.

Складові :

• мідний купорос (Купрум (ІІ) сульфат) – можна знайти в магазинчиках

 

“Все для квітів” як засіб боротьби зі шкідниками в фасуванні по 200 гр (на

декілька кристалів розміром до 5 см вистачить), орієнтовна вартість – 15 грн.

•         чиста фільтрована вода (можна взяти питну).
•         скляна тара – наприклад літрова чи півлітрова банка
•         тонка нитка (шовк наприклад) та водостійкий клей

Послідовність:

• Розчиняємо сіль (в нашому випадку мідний купорос) в гарячій воді – бо в гарячій воді може розчинитися більша кількість солі, а отже, скоріш буде відбуватися процес кристалізації, окрім того, ще й більшим може вирости кристал за один раз. В тенетах є варіанти вирощування коли спочатку вирощують маленький правильний кристал і потім ще раз готують новий розчин і цей кристалик стає затравкою для росту великого кристала, ми так не робили – хотіли різних кристалів)
•  Коли ми додали сіль до гарячої води – варто дочекатися, щоб сіль повністю розчинилася,  оскільки нерозчинені крупинки можуть стати невдалим центром кристалізації. Щоб цього уникнути зовсім – варто навіть після повного розчинення солі профільтрувати її крізь фільтрувальний папір. Ми цього  не робили, бо брали хімічно чистий мідний купорос та чисту питну воду.
• Коли розчин повністю готовий, тобто скільки б солі ви не додавали – вона вже не розчиняється в гарячій воді навіть при інтенсивному розмішуванні, переливаєте (чи фільтруєте) розчин солі в той посуд (банку в нашому випадку) де буде відбуватися вирощування кристалів. До цього часу або одразу після цього слід зробити затравку – те, на чому буде рости кристал.

Термін реалізації: один місяць.

Очікувані результати: вирощування кристалів захоплююче заняття, яке викликає  інтерес до таких наук, як хімія і фізика.

Практичне значення:  виконана робота має теоретичне та практичне значення і може використовуватись на уроках хімії, математики, географії, біології. Можна використати при поясненні  тем: “Поширеність у природі та використання  основних класів неорганічних сполук”,  “Кристалогідрати”, “Насичені і ненасичені розчини”, “Кристалічні гратки”, при проведенні позакласних та позаурочних заходів з природничих предметів.

Кінцевий результат:

• вирощені кристали мідного купоросу та натрій хлориду;
• результати досліджень про способи вирощування кристалів.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Підсумок

             Впровадження елементів STEM-освіти в навчанні математики та  хімії дає можливість підвищити якість науково-технологічної підготовки учнів, що в подальшому сприятиме підвищенню їх життєвих компетентностей і створює умови для досягнення високої мотивації навчання, забезпечення індивідуалізації процесу навчання.

           Моделювання багатогранників сприяє розвитку просторових уявлень, конструкторських раціоналізаторських здібностей. Під час проекту  ознайомилися  історію багатогранників, їх види, а також застосування. В ході дослідження розкрили  таємниці моделювання багатогранників, навчилися виготовляти різні моделі багатогранників. Правильні многогранники існували на Землі задовго до появи на ній людини – куби кам’яної солі, тетраедри сурм’янистого сірчанокислого натрію, октаедри  хромових кварців, ісокаедри бору, додекаедри радіолярію та мікроскопічнтх морських організмів. Геометрія з її прозорою логікою, чіткістю побудов відкрила зовсім нове бачення правильних многогранників та їх нове застосування.

 

 

Список використаних джерел

1. Бескид Л.М., Бескид В.Л. Многогранники. – К.: Вища школа,1984.
2. Глейзер Г.І. Історія математики в школі . – М. : Освіта, 1982.
3. Математика ( Шкільний світ).- 2002. –  №18; №22-23.
4. Математика в школах України. – 2002. –  №5; №11,12

Інтернет-ресурси

1. Кристал. – Режим доступу: https://uk.wikipedia.org/wiki/%D0%9A%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB
2. Кристалічні ґратки. Атомні, молекулярні та йонні кристали. – Режим доступу: https://subject.com.ua/master/Chemistry/lesson16.html
3.  Рідкі кристали. – Режим доступу: https://uk.wikipedia.org/wiki/%D0%A0%D1%96%D0%B4%D0%BA%D1%96_%D0%BA%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D0%B8
4. Рідкі кристали та їх використання. – Режим доступу: https://www.youtube.com/watch?v=UuSmVAGroVE
5. Український кристалічний щит. Режим доступу: https://uk.wikipedia.org/wiki/%D0%A3%D0%BA%D1%80%D0%B0%D1%97%D0%BD%D1%81%D1%8C%D0%BA%D0%B8%D0%B9_%D0%BA%D1%80%D0%B8%D1%81%D1%82%D0%B0%D0%BB%D1%96%D1%87%D0%BD%D0%B8%D0%B9_%D1%89%D0%B8%D1%82
6. Вирощування штучного кристала рубіна. – Режим доступу:

http://jak-zarobyty.pp.ua/5124-viroschuvannya-shtuchnogo-kristala-rubna.html

7. Вирощування кристалів. – Режим доступу: https://www.youtube.com/watch?v=IM6tBi6OIXY
8. Вирощування кристалів. – Режим доступу: https://www.youtube.com/watch?v=-Q5EFuzreyY
9. Як виростити кристали у мушлях. – Режим доступу: https://www.youtube.com/watch?v=cgeCHNyosg4

 

 

 

 

 

 

 

Підсумок

Освіта – дзеркало майбутнього країни. Залежно від того, у чому держава вбачає свої переваги, зони росту, вона коригує національну освітню програму, аж до самих підвалин системи освіти. У добу індустріалізації важливі були грамотність і володіння робітничими навичками. У постіндустріальну епоху на перший план вийшли технологічні аспекти розвитку молоді. Результатом стала цифрова революція – з інтернетом, повсюдним використанням комп’ютерів, інформаційних технологій. 

Стрімка еволюція технологій веде до того, що незабаром найбільш популярними та перспективними на планеті фахівцями стануть програмісти, IT-фахівці, інженери, професіонали в галузі високих технологій і т.д. У віддаленому майбутньому з'являться професії, про які зараз навіть уявити важко, всі вони будуть пов'язані з технологією і високо технологічним виробництвом на стику з природничими науками. Особливо будуть затребувані фахівці біо- та нано-технологій.

Постає питання – як підготувати таких фахівців? Навчання – це не просто передача знань від учителя до учнів, це спосіб розширення свідомості і зміни реальності.

У STEM-освіті активно розвивається креативний напрямок, що включає творчі та художні дисципліни (промисловий дизайн, архітектура та індустріальна естетика і т.д.). Тому що майбутнє, засноване виключно на науці, навряд чи когось порадує. Але майбутнє, яке втілює синтез науки і мистецтва, хвилює нас вже зараз. Саме тому вже сьогодні потрібно думати, як виховати кращих представників майбутнього.

STEM-технології вимагають від учнів великих здібностей до критичного мислення, вміння працювати як в команді так і самостійно. У нашій школі при вивченні багатьох дисциплін: математики, хімії, географії,фізики, біології –  безпосередньо вже зроблені перші кроки впровадження системи навчання STEM, інтегровані заняття спонукають до осмислення й пошуку причинно-наслідкових зв’язків, до розвитку логіки, мислення, комунікативних здібностей.

Для кожного вчителя,  який веде STEM-предмет, метою  має стати мотивування та зацікавлення учнів. Чим різноманітнішими і цікавішими будуть уроки, тим більше дітей захопляться цими предметами.

Упровадження елементів STEM-освіти в навчанні математики та географії дає можливість підвищити якість науково-технологічної підготовки учнів, що в подальшому сприятиме підвищенню їх життєвих компетентностей і створює умови для досягнення високої мотивації навчання, забезпечення індивідуалізації процесу навчання.

У перспективі – дослідження у напрямку використання GeoGebra в розробці STEM-проектів з теорії ймовірностей та математичної статистики з метою покращення ефективності процесу навчання природничо-математичних дисциплін.

На жаль, уроки теорії, які не викликають інтересу, – реалії більшості нинішніх шкіл. Вони переважно нудні для дітей. Адже протягом занять учні вивчають теоретичні відомості, численні формули, але практично не мають уявлення, як це насправді працює, і де всі ці знання можна використати у повсякденному житті! Уроки фактично позбавлені практичних занять, творчості та будь-яких експериментів!

У порівнянні з нинішнім, STEM-підхід є значно ефективнішим в організації освітнього процесу. Бо саме такий формат навчання дозволяє поєднувати опанування теорії з із напрацюванням навичок застосування цих знань у повсякденному житті. При цьому навчання шляхом моделювання, проектування та експериментування перетворюється на своєрідну гру, тому сприймається школярами із захопленням!

Новий підхід не є ексклюзивним: це не прерогатива «технологій», «математики», «науки» та «інженерії» як таких. STEM можна знайти в кожному аспекті життя. Методика може бути застосована практично до будь-якої дисципліни, де б її не викладали – чи то в молодшій школі, чи у вищій. Філософія STEM далеко пішла від застарілої концепції навчання, коли учні запам’ятовують факти, а їхні знання перевіряють за допомогою тестів із проставлянням оцінок.

Але ж і STEM не панацея: це лише інструмент, що допомагає учням зробити перший крок на шляху розуміння комплексності світу, усвідомлення багаторівневих зв’язків між різними аспектами життя. Згодом концепції, що сьогодні є свіжими та часто революційними, зокрема STEM,  і будь-які інші, стануть буденністю і нам доведеться винаходити щось нове. Але навіть сьогодні можна упевнено сказати, що методики освіти майбутнього охоплюватимуть не тільки науку і математику, а й філософію, мистецтво, розуміння природи людини та її місця у світі.

Міністерство освіти та науки у 2016 році опублікувало першу версію «Концептуальних засад реформування середньої освіти» та Концепцію Нової Української Школи (НУШ), де одними із основних компетентностей школярів є:

• Уміння логічно і математично мислити;
• Наукове розуміння природи і сучасних технологій;
• Впевнене користування інформаційно-комунікаційними технологіями;
• Обізнаність і самовираження у сфері культури.

Важливо долучити до змін і вчителів, які мають стати справжніми агентами змін освітньої реформи.