ВІДОКРЕМЛЕНИЙ СТРУКТУРНИЙ ПІДРОЗДІЛ

«ЗАПОРІЗЬКИЙ ЕЛЕКТРТЕХНІЧНИЙ ФАХОВИЙ КОЛЕДЖ

НАЦІОНАЛЬНОГО УНІВЕРСИТЕТУ «ЗАПОРІЗЬКА ПОЛІТЕХНІКА»

 

 

ЗАТВЕРДЖЕНО

Протокол засідання

ЦК спеціальності 133 Галузеве машинобудування від «_____»________2021р. №____

Голова ЦК__________Ганна ТАРАСОВА

 

 

 

 

 

 

 

 

 

 

ТЕХНІЧНА МЕХАНІКА

Збірник методичних  вказівок до лабораторних  робіт для всіх  спеціальностей 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Викладач                                                                                          І.В. Дубовський

 

 

 

 

 

2021

Передмова

 

Збірник методичних вказівок призначений для студентів денної та заочної форми навчання спеціальностей: 141 Електроенергетика та електромеханіка,         133 Галузеве машинобудування і 171 Електроніка. Метою виконання лабораторних робіт є допомога студентам у поглибленні та закріпленні теоретичних знань з предмету «Технічна механіка».

Методичні вказівки створені у відповідності до робочої начальної програми предмету, який охоплює три блоки: «Теоретична механіка», «Опір матеріалів», «Деталі машин».

Збірник складається з восьми методичних вказівок до лабораторних робіт. Структурні підрозділи кожної методичної вказівки подібні. Завдання до лабораторних робіт студенти отримують напередодні перед виконанням роботи.

Лабораторні роботи виконуються  за графіком після вивчення відповідних тем предмету. При їх виконанні слід використовувати навчальну літературу, діючі моделі, випробувальні машини, зразки деталей та вузлів, інші інформаційні матеріали в лабораторії.

Звіти з кожної лабораторної роботи оформлюються  за вимогами стандартів і захищаються кожним студентом індивідуально. Текст звіту пишеться на стандартних аркушах формату А4 з основним написом. Звіт складається з теми та мети роботи, необхідних рисунків, таблиць і розрахунків. Таблиці, схеми, рисунки, графічні залежності зображуються олівцем за допомогою креслярських приладів. У звіт слід включити необхідні для розрахунків формули та розрахункові величини згідно дослідам та висновки у відповідності з метою лабораторної роботи. При захисті звіту студент повинен відповісти на  контрольні питання теоретичного та практичного характеру, що стосуються теми даної роботи. 

Після завершення курсу з лабораторних робіт кожним студентом окремі звіти об’єднуються в альбом звітів з лабораторних робіт.

          

ЗМІСТ

Вступ ......................................................................................................................... 4 Лабораторна робота № 1.1 ..................................................................................... 5

1 Тема ....................................................................................................................... 5

Визначення центра ваги складної однорідної пластини методом

підвішування .................................................................................................................... 5 Лабораторна робота № 1.2 ..................................................................................... 9

1 Тема ....................................................................................................................... 9

Перевірка законів тертя; визначення кута тертя і коефіцієнта тертя ковзання ............................................................................................................................ 9

Лабораторна робота № 2 ...................................................................................... 12

1 Тема ..................................................................................................................... 12

Вивчення конструкцій одноступінчастих механічних передач ....................... 12

Лабораторна робота № 3 ...................................................................................... 15

1 Тема ..................................................................................................................... 15

Механічні випробування на розтяг зразка із низьковуглецевої сталі ............. 15

Лабораторна робота № 4 ...................................................................................... 18

1 Тема ..................................................................................................................... 18

Визначення лінійних переміщень поперечних перерізів балок при згині ................................................................................................................................ 18

Список літератури ................................................................................................. 22

Вступ

 

Успішний розвиток будь-якої галузі техніки залежить від рівня професійної підготовки спеціалістів, які в ній працюють. Високий рівень теоретичної підготовки ґрунтується на вивченні різних технічних наук, до яких відноситься технічна механіка, яка складається із трьох інженерних предметів: теоретичної механіки, опору матеріалів і деталей машин.

Відомо, що критерієм істинності знань у науці є експериментальна перевірка теоретично сформульованих законів або тверджень. Тому студенти повинні закріпити отримані теоретичні знання шляхом виконання лабораторних робіт у відповідності з робочою навчальною програмою спеціальності.

Наприклад, при виконанні лабораторної роботи, пов’язаної з визначенням центра ваги складної пластини студенти на практиці закріплюють поняття про рівновагу твердих тіл та умови рівноваги, щоб згодом використати набуті навички при розв’язку задач з теоретичної механіки і опору матеріалів. 

При виконанні лабораторної роботи, пов’язаних з механічними випробуваннями зразків із різних матеріалів на розтяг, студенти на практиці закріплюють знання про механічні властивості матеріалів, що дуже важливо знати при розрахунках різних деталей на міцність за формулами опору матеріалів та при виконанні курсових робіт за фахом.

При виконанні лабораторної роботи, пов’язаної з визначенням лінійних переміщень балки при згині закріплюються знання про основні фактори які впливають на деформації виробів та впевненість, що при ретельному проведенні експерименту на відповідному устаткуванні підтверджуються теоретичні знання щодо досліджуваної величини.

При виконанні лабораторної роботи, пов’язаних з вивченням конструкцій одноступінчастих механічних передач, студенти поглиблюють знання про склад, принцип роботи та призначення дуже  поширених у машинобудуванні різних механізмів та їх деталей і вузлів, а також отримують попередні поняття про кінематичні схеми різних приводів.

Виконання лабораторних робіт з технічної механіки забезпечує успішну роботу студентів при проходженні навчальної практики в механічних майстернях коледжу.

Лабораторна робота № 1.1

 

1   Тема

Визначення центра ваги складної однорідної пластини методом підвішування

 

2   Мета

                Визначити    центр     ваги    складної    пластини    практичним    способом,

познайомитися з властивостями центра ваги

 

3   Загальні відомості

Центром ваги називають єдину точку у будь-якому тілі, яка є центром його рівноваги: якщо тіло підвісити за цю точку, або оперти на неї, воно буде знаходитись у горизонтальному положенні і не перекидатись. У точці С (так позначають центр ваги тіла) прикладена сила тяжіння G, з якою тіло притягується до Землі.

Центр ваги тіла, складної пластини або складного перерізу можна визначити двома способами: практичним чи аналітичним. Практичний спосіб полягає у тому, що центр ваги легко визначити, якщо два або три рази підвісити тіло, провести лінії підвісу − центр ваги завжди буде знаходитися на перетині двох або трьох ліній підвісу. Лінії підвісу розташовані завжди вертикально вниз − до центру Землі, у напрямі сили тяжіння G (рисунок 1.1).

                                                                       

 

 

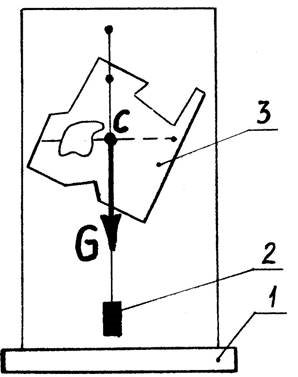
1 − установка для досліду; 2 −  гирька для натягування нитки; 

3 − складна однорідна пластина

 

Рисунок 1.1 − Лінії підвісу, центр ваги пластини і сили тяжіння G

 

Аналітичний спосіб полягає у визначенні координат точки С за формулами.

Цей спосіб розглядається окремо при виконанні розрахунково-графічної роботи.

При виконанні лабораторної роботи, або розрахунково-графічної роботи. треба знати такі властивості центра ваги:

− якщо предмет має вісь симетрії або дві вісі симетрії, то центр ваги завжди знаходиться на цій вісі або у точці перетину вісей симетрії (круг, кільце, прямокутник, квадрат, двотавр, швелер тощо);

− центр ваги тіла або пластини може знаходитись поза матеріальною частиною тіла: в цьому випадку точку опори треба створити штучно − на перетині двох натягнених ниток або дротинок, які співпадають з лініями підвісу;

− центр ваги тіла (точка С) займає постійне положення в межах тіла або пластині при будь-якому їх розташуванні у просторі;

− центр ваги тіла завжди намагається розташуватись найближче до центру Землі.

Знання цих властивостей дає змогу перевірити правильність визначення центра ваги і зменшити обсяг обчислень у два рази при застосуванні аналітичного способу при рішенні задач.

 

4   Технічне забезпечення

4.1             Установка для досліду.

4.2             Складні однорідні пластини.

4.3             Лінійка.

4.4             Плакати.

 

5   Послідовність виконання

5.1             Вирізати  із однорідного матеріалу − картону, фанери, оргскла, пластмаси, листового металу тощо складну пластину довільної форми, габаритні розміри якої не повинні перевищувати 160×160 мм (рисунок 1.2)

5.2             Зробити по контуру пластини два або три отвори діаметром 5 мм, за які послідовно підвісити пластину на дослідній установці. На пластині нарисувати 2 або 3 ліній підвісу, які співпадають з натягнутою ниткою, до якої підвішена гирька (рисунок 1.1).

5.3             Точку перетину лінії підвісу позначити буквою С − це і є центр ваги даної пластини (рисунок 1.1). Щоб впевнитись у цьому, досить обперти пластину на вертикально поставлений олівець − пластина повинна знаходитись у горизонтальному положенні.

5.4             Покласти пластину на аркуш формату А 4, олівцем обвести контур пластини, чим-небудь гострим перенести точку С з пластини  на її креслення (рисунок 1.3).

5.5             Провести координатні вісі X і Y так, щоб вони дотикалися зліва і внизу до контуру пластини, тобто креслення пластини повинне бути першій чверті координатної системи XOY ; позначити початок координат − точку O (рисунок 1.3).

 

 

 

 

 

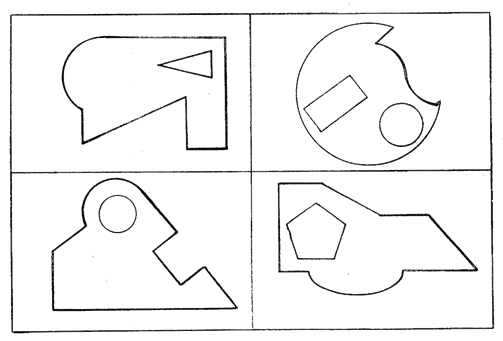
Рисунок 1.2 − Зразки складних пластин довільної форми

 

5.6             Для визначення координат X і Y точки С опустити із  цієї точки перпендикуляри  на  вісі  X та Y ,  позначивши  їх  X_C і Y_C відповідно  (рисунок

1.3).

5.7 Лінійкою виміряти значення координат X_C і Y_C у міліметрах, результати записати у таблицю 1.1.

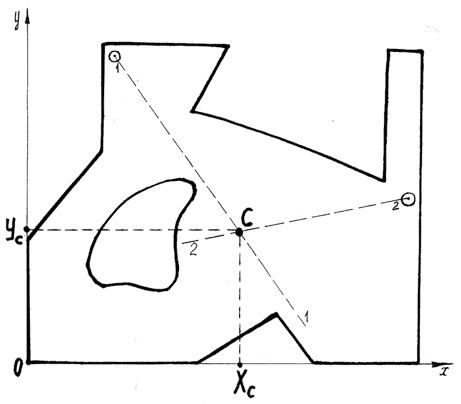
Рисунок 1.3 − Ескіз дослідної пластини

Таблиця 1.1 − Результати досліду

 

Координати центра ваги пластини	XC, мм	YC, мм

 

 

5.8 Пластину підписати і приєднати до звіту з лабораторної роботи.

5.9 Скласти висновок про виконану роботу.

 

6 Контрольні питання

6.1 Яка точка в мережах тіла або пластини має назву − центр ваги?

6.2 Дайте перелік властивостей центра ваги.

6.3 У чому полягає умова стійкості тіла проти перекидання?

Лабораторна робота № 1.2

 

1   Тема

Перевірка законів тертя; визначення кута тертя і коефіцієнта тертя ковзання

 

2   Мета

Навчитися визначати коефіцієнти тертя ковзання між різними матеріалами при сухому режими тертя.

 

3   Загальні відомості

Розглянемо тіло, яке лежить на шорсткій похилій площині, яка утворює кут α з горизонтальною площиною. Розкладемо силу тяжіння тіла G на складові G₁

G₁ та G₂: G₁ − паралельну похилій площині, ^G₂ − перпендикулярну до похилої площини. Модулі цих складових визначимо за формулами відповідно до рисунка

2.1:

 

G₁ = G sinα,

 

G₂ = Gcosα.

 

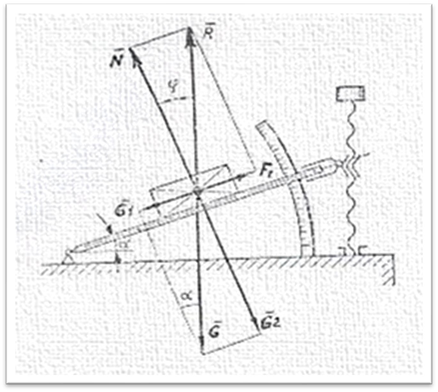
Рисунок 1.1 − Схема сил при русі тіла вниз по похилій площині під дією власної сили тяжіння

 

Складова G₂ врівноважується нормальною реакцією N похилої площини

G₂ = N = Gcosα

 

Складова G₁ намагається зрушити тіло вниз по похилій площині. Ця складова частково або повністю врівноважується силою тертя F_T . За основним законом тертя ковзання її максимальна величина визначається за формулою:

 

F_T = fN = fGcosα,

 

де f − коефіцієнт тертя ковзання між матеріалами тіла та похилої

площини.

Щоб тіло на похилій площині було у рівновазі, рушійна сила G₁ має дорівнювати за модулем силі тертя F_T , тобто

 

G₁ = Gsinα= fGcosα= F_T

 

Звідкіля коефіцієнт тертя ковзання можна визначити за формулою

 

Gsinα

                                                                              f =  = tgα= tgϕ,

Gcosα

 

де ϕ − кут тертя, кут між повною реакцією R (R=N+F_T ) і нормальною

реакцією N (рисунок 2.1).

Виходить, що α=ϕ, тоді f = tgϕ.

Якщо кут α між похилою площиною і горизонтом дорівнює куту тертя ϕ то тіло, яке лежить на похилій площині буде нерухомим, тобто перебувати у стані спокою, або рівномірно сковзатиме вниз. Умовою руху тіла під дією власної сили тяжіння є така нерівність:

 

α>ϕ,

або

G1>FT

 

Для експериментального визначення коефіцієнта тертя ковзання користуються похилою площиною із змінним кутом нахилу до горизонту − збільшують кут нахилу площини до тих пір, поки тіло не почне рухатися вниз під дією власної ваги. Коефіцієнт тертя ковзання f визначають як тангенс кута α нахилу площини в момент початку руху тіла. Кут α визначають за допомогою шкали на приладі (рисунок 1.1).

Коефіцієнт тертя ковзання f − величина безрозмірна. Його значення залежить від матеріалів площини та рухомого тіла, від якості обробки поверхонь, наявності мастила та його густини. Для різних матеріалів і різних умов середні значення коефіцієнтів тертя знаходяться в довідниках, наприклад:

− сталь по кризі − f = 0,02; − дерево по дереву − f = 0,60; − метал по металу − f = 0,30. 4 Технічне забезпечення 4.1  Прилад для досліду.

4.2 Зразки тіл із різних матеріалів.

4.3 Мікрокалькулятор.

 

5   Послідовність виконання

5.1             Підготувати прилад до досліду.

5.2             Покласти зразок на площину, повільно нахиляти її доти, поки зразок не почне ковзати вниз.

5.3             Записати в таблицю 1.1 значення кута нахилу α в момент початку руху тіла вниз по площині.

5.4             Визначити величину коефіцієнту тертя ковзання за формулою:

 

f = tgϕ

 

5.5             Повторити дослід з усіма зразками із різних матеріалів, заповнити таблицю 2.1.

5.6             Скласти висновки.

 

Таблиця 1.1 − Результати досліду

 

Матеріал площини			Сталь
Матеріал зразків	сталь	деревина	чавун	алюміній	латунь
Кут тертя ϕ, град.
Коефіцієнт тертя f

 

 

6   Контрольні питання

6.1             Сформулюйте основний закон тертя ковзання (закон Кулона).

6.2             Назвіть фактори, які впливають на коефіцієнт тертя ковзання.

6.3             Напишіть умову рівноваги тіла на похилій площині.

6.4             Назвіть основні відмінності тертя ковзання від тертя кочення.

6.5             Надайте приклади числових значень коефіцієнтів тертя ковзання та коефіцієнтів тертя кочення (для порівняння) для різних пар матеріалів.

Лабораторна робота № 2

 

1   Тема

Вивчення конструкцій одноступінчастих механічних передач 

 

2   Мета

2.1             Познайомитись з особливостями конструкцій  одноступінчастих механічних передач.

2.2             Навчитись зображувати кінематичні схеми механічних передач у відповідності до ГОСТ 2.703 − 68.

2.3             Визначити передаточні числа одноступінчастих передач − редукторів.

 

3   Технічне забезпечення

3.1             Моделі зубчастих, черв’ячних, ланцюгових і пасових передач − редукторів.

3.2             Штангенциркуль.

3.3             Мікрокалькулятор.

 

4   Порядок виконання

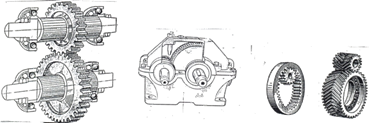
4.1             Познайомитись з конструкціями одноступінчастих механічних передач − редукторів: зубчастого циліндричного редуктора, зубчастого конічного редуктора, черв’ячного закритого редуктора, ланцюгової та клинопасової передач, використавши моделі названих механічних передач (рисунок 2.1).

4.2             Зобразити кінематичні схеми механічних передач  у  відповідності до ГОСТ 2.703 − 68.

4.3             Скласти стислий опис кожної зображеної механічної передачі.

4.4             Визначити  основні параметри  ведучого та веденого коліс: числа зубів  Z₁ і Z₂ − для зубчастих передач, d₁ і d₂ мм, − для пасових або фрикційних передач.

Діаметри шківів або котків виміряти штангенциркулем.

4.5             Обчислити передаточне число u кожної передачі за формулами:

 

u = Z²  або  u=^d2 ,

                                                                                           Z1                 d₁

 

де Z₁ − число зубів на ведучому зубчастому колесі (шестерні), або число

заходів різьби на черв’ячному гвинті;

Z₂ − число зубів на веденому зубчастому колесі; d₁ і d₂, мм − діаметри ведучого та веденого коліс (шківів або котків)

відповідно.

4.6             Виконати графічну частину роботи відповідно до пункту 2.2. приклади зображення кінематичних схем одноступінчастих передач показані на рисунку 2.2.

4.7             Виконати пункт 4.3, користуючись рисунком 2.2.

4.8             Результати дослідів записати до таблиці 2.1.

 

а

 

б

 

в

 

г

 

д

 

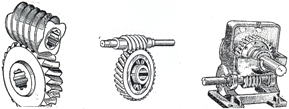
ж

 е

а) фрикційні ; б) пасові; в) циліндричні зубчасті; г) конічні зубчасті; д) гвинтові; е) черв’ячні; ж) ланцюгові.

 

Рисунок 2.1 − Загальний вигляд одноступінчастих механічних передач

           

 

 

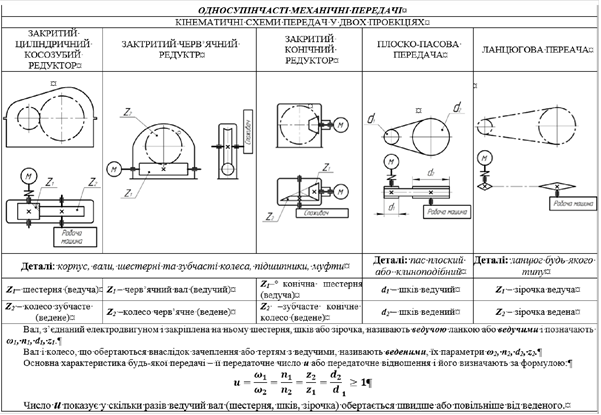
Рисунок 2.2 − Приклади зображення кінематичних схем механічних передач

 

Таблиця 2.1 − Результати дослідів

 

Назва передачі	Числа зубів		Діаметри колес		Передаточне число передачі u
	ведуча шестерня Z1	ведене колесо Z2	Ведучого шківа(котка) d1, мм	Веденого шківа (котка) d2, мм

 

5   Контрольні питання

5.1  Яка основна мета застосування передач − редукторів у техніці?

5.2  Назвіть деталі кожної механічної передачі?

5.3  Яка ланка у механізмі називається ведучою, а яка веденою?

5.4  Що показує передаточне число редуктора?

           

 

Лабораторна робота № 3

 

1   Тема

Механічні випробування на розтяг зразка із низьковуглецевої сталі

 

2   Мета

Ознайомитись      з        методикою визначення основних    механічних характеристик сталі при розтягу в умовах статичного навантаження.

3   Технічне забезпечення

3.1             Випробувальна машина ИМ − 4Р.

3.2             Зразок із сталі для випробування.

3.3             Штангенциркуль, лінійка.

3.4             Мікрокалькулятор.

4   Завдання

4.1             Одержати діаграму розтягу в осях: сила F − деформація ∆l .

4.2             Визначити основні механічні характеристики матеріалу зразка (рисунки 3.1 та 3.2): границю текучості σ_T , границю міцності σ_МЦ , характеристики пластичності δ і Ψ.

4.3             Уточнити марку сталі зразка за допомогою таблиці 3.4.

5   Послідовність виконання 

5.1             Ознайомитись з конструкцією випробувальної машини та пристроєм для закріплення зразка.

5.2             Зобразити необхідні рисунки та підготувати таблиці для запису результатів вимірювань і обчислень.

 

 

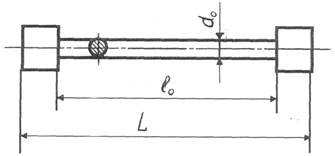
Рисунок 3.1 − Зразок до початку випробувань

 

5.3             Спостерігати процес розтягу зразка із сталі при статичному навантаженні  та  одночасне автоматичне  зображення машинної діаграми розтягу в осях F − ∆l .

5.4             Звернути увагу на зразок при появі на ньому місцевого звуження − шийки, що вказує на початок руйнування зразка.

5.5             Визначити  на отриманій машинній діаграмі характерні точки 1, 2, 3, 4 і їх координати. Масштаб на осях діаграми: на вісі F − у 1 мм − 100 Н (тобто 1:100); на вісі ∆l − у 100 мм − 1 мм (тобто 100:1).

5.6             Результати досліду записати до таблиць 3.1 та 3.2.

 

 

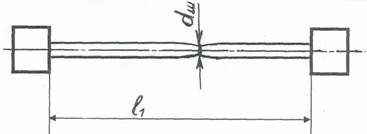
Рисунок 3.2 − Зразок після випробування

 

Таблиця 3.1 − Результати вимірювань зразка

 

Характеристика зразка	Довжина зразка, мм	Діаметр зразка, мм	Площа поперечного перерізу, мм2
До випробування	l0 =	d0 =	πd2 = А0                 0 = 4
Після випробування	l1 =	dШ =	πd2 АШ = Ш = 4

 

Таблиця 3.2 − Результати обробки машинної діаграми випробуваного зразка

 

Характерні точки діаграми	Сила F , Н	Абсолютне видовження ∆l , мм	Нормальні напруги σ, МПа
1 − границя пропорційності	F1 =	∆l1 =	σПЦ	F = 1 = A0
2 − границя текучості	F2 =	∆l2 =	σТ =	F2 = A0
3 − границя міцності	F3 = Fmax =	∆l3 =	σМЦ	Fmax =          = A0
4 − момент розриву зразка	F4 =	∆l4 =	F σP = 4 = AШ

 

Таблиця 3.3 − Характеристики  пластичності  матеріалу

 

Абсолютне видовження зразка, мм	∆l = l1 − l0 =
Відносне залишкове видовження, %	l − δ= 1             l0 ×10000 = l0
Відносне залишкове звуження, %	A − Ψ= 0 AШ ×10000 = A0

Таблиця 3.4 − Механічні властивості сталей при розтягу

 

Види та марки сталей	Границя міцності σМЦ (σB ), МПа	Границя текучості σT , МПа
Вуглецеві сталі звичайної якості ГОСТ 380−88 Ст.2 Ст.3 Ст.4 Ст.5	320 − 400 380 − 470 420 − 520 500 − 620	190 − 220 210 − 240 240 − 260 260 − 280
Вуглецеві сталі якісні ГОСТ 1050−88 20 30 40 45 50	420 − 500 500 − 600 580 − 700 610 − 750 640 − 800	250 300 340 360 380
Леговані сталі  ГОСТ 4543−61 20Х 40Х 45Х 40ХН	720 − 850 730 − 1050 850 − 1050 1000 − 1450	400 − 650 650 − 900 700 − 950 800 − 1300

 

 

6   Контрольні питання

6.1             Які характеристики матеріалів визначають при випробуванні зразків на розтяг?

6.2             Яку напругу називають границею міцності?

6.3             Запишіть закон Гука, дайте характеристику величин, що входять до нього.

6.4             Чому напруга в момент розриву зразка значно більша, ніж границя міцності матеріалу зразка?

6.5             Навіщо треба мати знання про механічні характеристики матеріалів?

Лабораторна робота № 4

 

1   Тема

Визначення лінійних переміщень поперечних перерізів балок при згині

 

2   Мета

Навчитись визначати стрілу прогину балки на двох опорах практичним способом, навчитись обчислювати значення стріли прогину за формулою та порівнювати отримані результати.

 

3   Загальні відомості

Окpiм розрахункiв на мiцнicть балки часто перевiряють або розраховують на жорсткiсть. Умова жорсткостi балки полягає у тому, що максимальний прогин − стріла прогину балки f не повинна перевищувати допустимої величини [^f ], тобто повинна виконуватись нерівність:

 

f ≤ [f ]

 

Величину допустимої стріли прогину [^f ] звичайно задають у частинах від довжини прольоту l балки:

[f ]= ()×l

Величина стріли прогину f залежить вiд таких факторів:

-   розрахунковою схеми балки;

-   довжини балки;

-   матеріалу балки;

-   величини зовнiшнiх навантажень (сил або моментів) i мiсця їх прикладення до балки;

-   способів закріплення кiнцiв балки (жорстке затиснення одного кiнця консольної балки або закріплення балки на двох шарнірних опорах);

-   форми поперечного перерізу балки (прямокутник, квадрат, круг, кiльце, двотавр, швелер);

-   розмірів перерізу;

-   розташування поперечного перерізу балки відносно діючих сил (на ребрі або плазом).

Наприклад: якщо обидва кiнцi балки закрiпленi шарнiрно, а сила F прикладена посередині її довжини, стрiла прогину f обчислюється за формулою:

Fl³

                                                                                              f = ,

48EJ

де F − сила, Н; l − довжина, мм;

E − модуль повздовжньої пружності матеріалу, МПа;

J − осьовий момент інерції поперечного перерізу J_X або J_Y , мм⁴;

 − коефіцієнт для даної розрахункової схеми балки.

 

4   Технічне забезпечення

4.1             Установка для досліду.

4.2             Зразки балок із різних матеріалів.

4.3             Штангенциркуль.

4.4             Мікрокалькулятор 

 

5   Послідовність виконання

5.1             Ознайомитись з конструкцією установки для досліду (рисунок 4.1).

5.2             Визначити необхідні  геометричні розміри балки: розрахункову довжину l і розміри  поперечного  перерізу b та h  прямокутної  форми (рисунок

4.2).

5.3 Уточнити матеріал зразка та модуль повздовжньої пружності E цього матеріалу за довідником або за таблицею 4.1.

5.4 Обчислити стрілу прогину балки для даної розрахункової схеми (рисунок 6.3) за формулою:

Fl³

                                                                                         fT =  ,

48EJ_X

b×h³

                  де J_X =  , мм⁴.

12

5.5 Визначити дослідне значення стріли прогину балки ^f_д за допомогою установки з вантажем, силу тяжіння якого позначити F ; величина f_д визначається за допомогою індикатора для вимірювання лінійних переміщень (рисунок 4.1):

 

fд =0,01× n ,

 

де n − число поділок на шкалі індикатора;

0,01 − ціна однієї поділки індикатора, мм.

5.6 Порівняти дослідне значення стріли прогину балки з обчисленим за теоретичною формулою, визначити похибку за формулою:

 

                                                                                             ft − fд               0

                                                                              δ=              ×1000 ,

f_д

 

де δ − величина похибки, яка не повинна перевищувати 10 %.

5.7 Результати вимірювань розмірів, обчислень та досліду записати до таблиці 6.2.

 

 

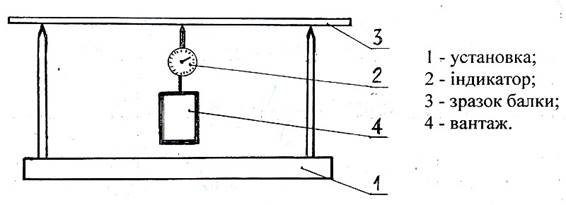
Рисунок 4.1 − Установка для досліду

 

 

 

Рисунок 4.2 − Балка прямокутного поперечного перерізу

 

 

 

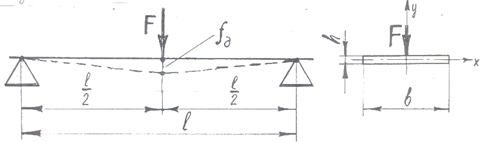
Рисунок 4.3 − Розрахункова схема балки

 

Таблиця 4.1 − Значення модулів повздовжньої пружності деяких матеріалів

 

Матеріал балки	Модуль пружності матеріалів Е, МПа
Сталь	(1,9…2,2)×105
Латунь, бронза	(1,,,1,15)×105
Алюміній	(0,7)×105
Склопластик	(0,18…0,35)×105
Гетинакс	(0,1…0,18)×105
Деревина	(0,07…0,18)×105
Текстоліт	(0,04…0,10)×105

Таблиця 4.2 − Результати вимірювань і досліду

 

Назва величини	Позначення	Числові значення
Розрахункова довжина балки, мм	l
Товщина балки, мм	h
Ширина балки, мм	b
Величина зосередженої сили − вага гирі, Н	F
Матеріал балки
Модуль пружності матеріалу балки, МПа	E
Момент      інерції         поперечного           перерізу балки, мм4	JX
Розрахункове значення стріли прогину балки, мм	ft
Число поділок на індикаторі після навантаження балки на дослідній установці	n
Дослідне значення стріли прогину балки, мм	fд
Величина похибки, %	δ

 

6   Контрольні питання

6.1             Написати напам'ять формулу для обчислення стріли прогину балки на двох опорах, навантаженої силою посередині, надати необхідні пояснення.

6.2             Назвати фактори, які впливають на жорсткість балки.

6.3             Чи зміниться величина стріли прогину дослідженої балки, якщо її повернути на 90⁰, залишивши розрахункову схему балки без змін?

           

 

Список літератури

1                    Олофинская В.П. Технічна механіка. Курс лекций с вариантами практических и тестовых заданий: учебное пособие . − М.: Форум, 2012. − 352 с.

2                    Олофинская В.П. Технічна механіка. Практические работы с краткими теоретическими сведениями и методические рекомендации: учебное пособие. –  М.: Неолит, 2017. – 168 с. – (Профессиональное образование).

2                    Рубашкин А.Г. и др. Руководство по проведению лабораторных работ по технической механике. − М.: Высшая школа, 1984. − 315 с.

3                    Аркуша И.И. и др. Техническая механика. − М.: Высшая школа, 1983. − 447 с.

5 Писаренко Г.С. и др. Справочник по сопротивлению материалов. − К.: Наукова думка, 1975. − 650 с.