27.01_Метричні співвідношення в прямокутному трикутнику. Властивість бісектриси

У ∆АСВ (∠С=90) СК⊥АВ, АК=4, КВ=9. Знайти СК

Знайти катет прямокутного трикутника, якщо його гіпотенуза дорівнює 27 см, а проекція шуканого катета на гіпотенузу - 3 см

Катет прямокутного трикутника дорівнює 8 см, а його проекція на гіпотенузу - 4см. Знайти гіпотенузу

Яка рівність є правильною для даного трикутника?
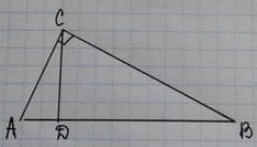
Проєкція катета BС на гіпотенузу
Знайти висоту прямокутного трикутника, проведену з вершини прямого кута, якщо вона поділяє гіпотенузу на відрізки завдовжки 4 см та 9 см.
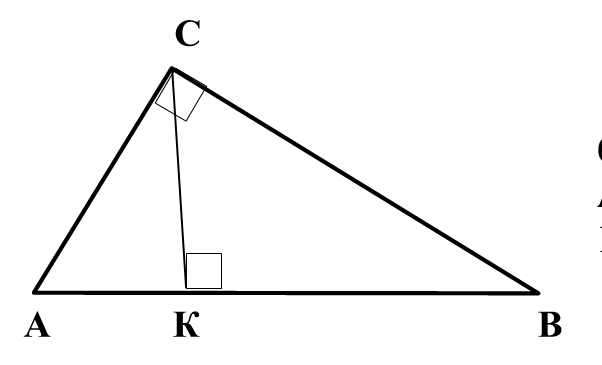
В прямокутному трикутнику АВС АК=18 см, КВ= 32 см. Знайдіть АС

В прямокутному трикутнику АВС АК=18 см, КВ= 32 см. Знайдіть ВС.

В прямокутному трикутнику АВС АК=18 см, КВ= 32 см. Знайдіть СК.
Знайти катет прямокутного трикутника, якщо його гіпотенуза дорівнює 12 см, а проєкція шуканого катета на гіпотенузу 3 см. Надати розв'язання
ВК – бісектриса трикутника АВС, АВ=8см, ВС=10см, АК=4см. Знайти АС.
Бісектриса трикутника ділить сторону на відрізки, різниця довжин яких дорівнює 2см. Знайти цю сторону, якщо дві інші сторони дорівнюють 6см і 10см.

Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома


















