Тестові завдання з математики для учнів 5 класів.

Тестові завдання № 1

з теми  «Натуральні числа»

Варіант 1

1.Виберіть правильний запис числа: десять мільйонів вісімдесят тисяч п’ять

    а)10085005; 

   б) 1085005;

в) 10805005;

г) 10850050;

2. Виберіть число, у якого 9 сотень 7 десятків:

   а) 907;

   б) 970;

   в) 9007.

3. Округліть число 12 475 836 до десятків:

   а) 12 475 84;

   б) 12 475 830;

   в) 12 475 8;

   г) 12 475 840.

4. Дано три числа: 359; 4 307; 801. Обчислити суму цих чисел і округлити результат до сотень

а) 5467 ≈5470;  

б) 5457 ≈5460; 

в) 5467 ≈5460; 

г) 5464 ≈5460.

5. Сто тридцять два мільйони двадцять п’ять тисяч триста п’ятдесят чотири записується як

   а) 132005354;

   б) 13225354;

   в) 132025354;

   г) 132250354.

Варіант 2

1.Виберіть правильний запис числа: дев′ять мільйонів вісімдесят тисяч п’ять

    а)9085005; 

   б) 985005;

в) 9805005;

г) 9850050;

2. Виберіть число, у якого 6 сотень 5 десятків:

   а) 605;

   б) 670;

   в) 6005;

   г)  650.

3. Округліть число 14 474 432 до десятків:

   а) 14 475 84;

   б) 14 475 420;

   в) 14474430;

   г) 14475 440.

4. Дано три числа: 350; 4 327; 803. Обчислити суму цих чисел і округлити результат до сотень

а) 5480 ≈5400;  

б) 5480 ≈5480; 

в) 5480 ≈5500; 

г) 5470 ≈5470.

5. Сто сорок три мільйони сімдесят п’ять тисяч двісті п’ятдесят чотири записується як

   а) 143750254;

   б) 143075254;

   в) 143705254;

   г) 14375254.

Тестові завдання № 2

з теми «Додавання і віднімання натуральних чисел

Варіант 1

1.               Як називається результат дії додавання?

    а) сума; 

   б) різниця;

в) добуток;

г) немає правильної відповіді;

 2. Як називається компонент дії віднімання, який стоїть на першому місці?

    а) доданок; 

   б) зменшуване;

в) різниця;

г) відє′мник;

 3. Виконайте додавання 11 139 + 78 661:

    а) 900000; 

   б) 89990;

в) 80000;

г) 90000;

4. Обчисліть на скільки число 59 428 більше від 400:   

   а) на 59128 

   б) на 58028;

в) на 59028;

г) на 590028.

   5. В овочесховищі  було 313 т  картоплі. У понеділок привезли на 187 т більше, ніж було в овочесховищі, а у вівторок – на 40 т менше, ніж привезли в понеділок. Скільки тон картоплі стало в овочесховищі? 

   а) 1270;

   б) 1273;

   в) 900;

   г)  1200.

Варіант 2

1. Як називається результат дії віднімання?

    а) сума; 

    б) різниця;

в) добуток;

г) немає правильної відповіді;

2. Як називається компонент дії віднімання, який стоїть на другому  місці?

    а) доданок; 

   б) зменшуване;

в) різниця;

г) відє′мник;

 3. Виконайте додавання 12 369 + 27 631:

    а) 400000; 

   б) 39990;

в) 40000;

г) 50000;

 4. Обчисліть на скільки число 59 428 більше від 9000:    

   а) на 59128 

   б) на 58028;

в) на 50428;

г) на 590028.

5. До будівельного майданчику привезли 340 т щебеню, а піску на 80 т більше. Цементу на 103 т менше, ніж піску. Скільки всього привезли будівельних матеріалів?

  а) 270;

   б) 976;

   в) 977;

   г)  120.

Тестові завдання № 3

з теми «Величини. Вирази. Формули. Рівняння

Варіант 1

1.               Подайте 4 м 5 см  у сантиметрах:

а) 405 см;

б) 45 см;

в) 450 см;

г) 4005 см.

2.               Знайдіть значення виразу 7 420 : х, якщо х = 20:

 а) 3701;

б) 371;

в) 271;

г) 361.

3.               Поїзд ішов 3 год. зі швидкістю V км/год. Який шлях пройшов поїзд? Обчисліть шлях, пройдений поїздом, якщо V = 15.

а) 35;

б) 50;

в) 45;

г) 44.

4.               У залі для глядачів кінотеатру в кожному ряді Х місць, а кількість рядів на 2 менша, ніж кількість місць у ряді. Скільки всього місць у залі для глядачів, якщо Х = 32?

а) 96;

б) 940;

в) 86;

г) 84.

 Варіант 2

1. Подайте 4 м 50 см  у сантиметрах:

а) 405 см;

б) 45 см;

в) 450 см;

г) 4005 см.

2.               Знайдіть значення виразу 7 420 : х, якщо х = 20:

 а) 3701;

б) 371;

в) 271;

г) 361.

3.               Поїзд ішов 4 год. зі швидкістю V км/год. Який шлях пройшов поїзд? Обчисліть шлях, пройдений поїздом, якщо V = 11.

а) 35;

б) 50;

в) 45;

г) 44.

4.               У залі для глядачів кінотеатру в кожному ряді Х місць, а кількість рядів на 2 менша, ніж кількість місць у ряді. Скільки всього місць у залі для глядачів, якщо Х = 22?

а) 440;

б) 94;

в) 86;

г) 84.

Тестові завдання № 4

з теми «Властивості множення натуральних чисел»

Варіант 1

1.               Запишіть переставний закон множення для довільних чисел х і у.

а) х - у = у - х;

б) х + у = у · х;

в) х · у = у · х;

г) х + у = у + х.

2.   1029 помножили на 11850 і отримали:

а) 121934; 

б) 12203560;   

в) 12193650; 

г) 12193558.

3. Спростіть вираз 41k  + 23k + k:       

а) 63 k;  б) 65 k; ;  

в) 55 k;            г) 66 k.

4.Знайдіть корені  рівняння (х – 2)(8 – х) = 0.

а) – 2 і 8 ;  б) 2 і 8 ; 

в) – 2 і  - 8;            г) 2 і - 8.

Варіант 2

1. Запишіть переставний закон множення для довільних чисел х і у.

а) х · у = у · х  ;

б) х + у = у · х;

в) х - у = у - х;

г) х + у = у + х.

2. 1039 помножили на 11860 і отримали:

а) 121934;   

б) 12322540;   

в) 12324540; 

г) 12193558.3.

3.Спростіть вираз 31k  + 23k + k:      

а) 63 k;  б) 65 k; ;  

в) 55 k;            г) 66 k.

4. Знайдіть корені  рівняння (х – 12)(4 – х) = 0.

а) – 12 і 4 ;  б) 12 і 4 ; 

в) – 12 і  - 4;            г)12 і - 4.

Тестові завдання № 5 

з теми «Ділення натуральних чисел»

Варіант 1

1.               Знайдіть значення виразу 42 : 7 + 15 · 3.

а) 52;  б) 50 ; 

в) 51;            г) 55.

2.               Спростіть вираз 218х – 198х і знайдіть його значення, якщо х = 14.

а) 260;  б) 270 ; 

в) 180;            г) 280.

3.               Розв’яжіть рівняння: 5z + z – 42 = 18.

а) z = 11;  б) z = 21; 

в) z = 10;            г) z = 1.

4.               Знайдіть значення виразу: 156 · 41 +62 · 41 – 18 · 41.

а) 7200;  б) 8002; 

в) 8020;            г) 8200

5.               Виконайте ділення з остачею 15 740 : 33 - результат округліть до десятків: 

а) 475;  б) 477 ;  

в) 476;            г) 474.

Варіант 2

1.          Знайдіть значення виразу 42 : 6 + 15 · 3.

а) 52;  б) 50 ; 

в) 51;            г) 55.

2.               Спростіть вираз 218х – 198х і знайдіть його значення, якщо х = 12.

а) 260;  б) 270 ; 

в) 180;            г) 240.

3.               Розв’яжіть рівняння: 6z + z – 22 = 48.

а) z = 11;  б) z = 21; 

в) z = 10;            г) z = 1.

4.               Знайдіть значення виразу: 155 · 21 +62 · 21 – 17 · 21.

а) 7200;  б) 4200; 

в) 4020;            г) 8200

5.               Виконайте ділення з остачею 15 740 : 23 - результат округліть до десятків:                                                        

а) 775;  б) 717 ;  

в) 716;            г) 715.

 Тестові завдання № 6 з теми «Многокутники»

Варіант 1

1.               На якому рисунку зображено прямокутний трикутник?

а)       :

б)

В)

Г) 

2. Визначте вид трикутника за його кутами 34°; 127°; 19°:

а) прямокутний  ;

б) тупокутній;

в) гострокутній;

г) не можна визначити.

3.               Одна сторона трикутника дорівнює 24 см, друга сторона на 16 см довша за першу, а третя у 2 рази коротша за другу. Знайти периметр трикутника.

а) 86 см ;

б) 84 см;

в) 74 см;

г) не можна визначити.

Варіант 2

1. На якому рисунку зображено прямокутний трикутник?

а)   

б)

В)  

Г) 

2. Визначте вид трикутника за його кутами 34°; 90°; 56°:

а) прямокутний  ;

б) тупокутній;

в) гострокутній;

г) не можна визначити.

3. Одна сторона трикутника дорівнює 22 см, друга сторона на 18 см довша за першу, а третя у 2 рази коротша за другу. Знайти периметр трикутника.

а) 86 см ;

б) 84 см;

в) 74 см;

г) не можна визначити.

Тестові завдання № 7

 з теми «Площа та об’єм»

Варіант 1

1. Виразіть в квадратних метрах 3 га

а) 30 м² ;

б) 300 м² ;

в) 3 м² ;

г) 30000 м² .

2.               Довжина прямокутника 25 дм, ширина 40 дм. Знайти площу прямокутника і виразити її у квадратних метрах.

а) 10 м² ;

б) 100 м² ;

в) 1000 м² ;

г) 1 м² .

3.               Ширина прямокутного паралелепіпеда дорівнює 10 см, довжина на 5 см більша, а висота – у три рази менша від довжини. Обчислити об’єм паралелепіпеда.

а) 650 м² ;

б) 600 м² ;

в) 700 м² ;

г) 750 м² .

4.               Об’єм куба з ребром 4 м дорівнює:

а) 65 м³ ;

б) 64 м³;

в) 75 м³;

г) 66 м³  .

Варіант 2

1. Виразіть в квадратних метрах 5 га

а) 5000 м² ;

б) 55000 м² ;

в) 50000 м² ;

г) 500 м² .

2. Довжина прямокутника 250 дм, ширина 4 дм. Знайти площу прямокутника і виразити її у квадратних метрах.

а) 10 м² ;

б) 100 м² ;

в) 1000 м² ;

г) 1 м² .

3.               Ширина прямокутного паралелепіпеда дорівнює 8 см, довжина на 7 см більша, а висота – у три рази менша від довжини. Обчислити об’єм паралелепіпеда.

а) 650 м² ;

б) 600 м² ;

в) 700 м² ;

г) 750 м² .

4. Об’єм куба з ребром 5 см дорівнює:

а) 65 см³ ;

б) 64 см³;

в) 75 см³;

г) 66 см³  .

Тестові завдання № 8

з теми «Порівняння звичайних дробів»

Варіант 1

1.               Дріб з чисельником 8 і знаменником 21 записується так

а);             б) ;             в) ;             г) .

2. Число у вигляді неправильного дробу записується так:

А) ;          Б) ;         В) ;.

3.Тетянка зібрала 28 грибів, з них грибів були білі. Скільки білих грибів зібрала Тетянка?

а) 21;             б) 18;             в) 20;             г) 24.

4.               Петрик, Олег і Сашко зібрали 96 горіхів. Петрик зібрав 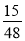усіх горіхів, а Сашко -  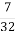  усіх горіхів. Скільки горіхів зібрав Олег.

а) 21;             б) 45;             в) 27;             г) 47.

Варіант 2

1. Дріб з чисельником 5 і знаменником 7 записується так:

а);             б) ;             в) ;             г) .

2. Число у вигляді неправильного дробу записується так:

А) ;          Б) ;         В) ;.

3.Петрик піймав 6 окунів, що становить усієї кількості риби, яку він піймав. Яку кількість риби піймав Петрик?

а) 21;             б) 18;             в) 12;             г) 24.

4.Наталка, Світлана та Юля збирали рослини для гербарію. Разом дівчатка зібрали 450 експонатів. Наталка зібрала усіх зібраних експонатів, Юля - усіх експонатів. Скільки експонатів зібрала Світлана?

а) 121;             б) 115;             в) 127;             г) 147.

Тестові завдання № 9

з теми «Додавання і віднімання дробів з однаковими знаменниками»

Варіант 1

1.   Виконайте дії та вкажіть найбільший отриманий результат:

а) ;

б) ;

в) ;

г) ;

д) .

2.   Розв’яжіть рівняння:      .

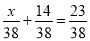а) 9; 

б) 7 ;

в) 5 ;

г) 10 .

3.   Дід Панас продав 240 кг. Картоплі. Першого дня було продано 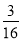картоплі, а другого дня - 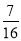. Скільки кілограмів картоплі було продано за два дні?

а) 19; 

б) 70 ;

в) 150 ;

г) 100 .

Варіант 2

1.               Виконайте дії Виконайте дії та вкажіть найбільший отриманий результат:

а) ;

б) ;

в) ;

г) ;

д) .

2. Розв’яжіть рівняння:      .

а) 18; 

б) 17 ;

в) 15 ;

г) 10

3.За перший місяць побудували дороги, а за другий - . Скільки кілометрів дороги було побудовано за два місяці, якщо довжина всієї дороги становить 92 км.

а) 190; 

б) 70 ;

в) 150 ;

 г) 60.

.