Тотожні перетворення раціональних виразів
Тема уроку. Тотожні перетворення раціональних виразів.
Мета. Домогтися засвоєння учнями змісту поняття «тотожні перетворення раціональних виразів» та схеми (алгоритму) перетворення раціонального виразу на раціональний дріб.
Тип уроку. Засвоєння знань та первинних умінь.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Зібрати зошити учнів із виконаним домашнім завданням на перевірку.
III. Формулювання мети і завдань уроку
Учитель повідомляє учням мету і завдання уроку
IV. Актуалізація опорних знань та вмінь
Виконання усних вправ
- При яких значеннях змінних дріб не має змісту?
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
При яких значеннях змінних цей дріб дорівнює нулю?
-
Подайте вираз у вигляді дробу: а)
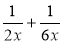 ; б)
; б)  ; в)
; в) 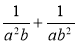 ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() .
.
- Які з рівностей є тотожностями. Чому?
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ?
?
V. Засвоєння знань
Тотожні перетворення раціональних виразів
- Перетворення будь-якого раціонального виразу можна звести до додавання, віднімання, множення та ділення раціональних дробів.
-
Суму, різницю, добуток і частку раціональних дробів завжди можна
подати у вигляді раціонального дробу. -
Будь-який раціональний вираз можна подати у вигляді раціонального
дробу. Для цього:
а) встановлюємо (визначаємо), які дії з раціональними дробами слід виконати, виходячи з умови завдання;
б) виконуємо ці дії або у порядку спадання дії, або користуючись законами (властивостями) арифметичних дій (перестановка + і; сполучна + і; розподільна) та властивостями раціональних дробів (основною властивістю дробу)
Приклад 1. Довести тотожність
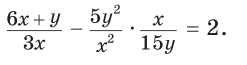
Розв’язання. Спростити ліву частину рівності:
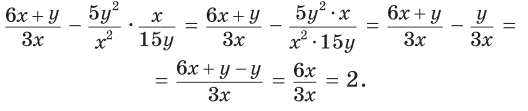
За допомогою тотожних перетворень звели ліву частину рівності до правої. Отже, рівність є тотожністю.
Приклад 2. Спростити вираз
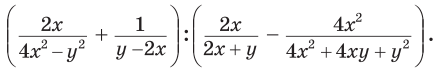
Розв’язання. Спочатку подамо вирази у кожній з дужок у вигляді дробів, а потім потім виконаємо ділення:
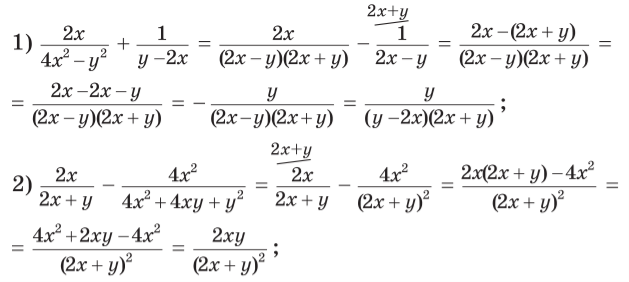
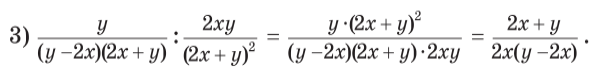
Запис розв’язання можна подати інакше:
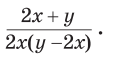
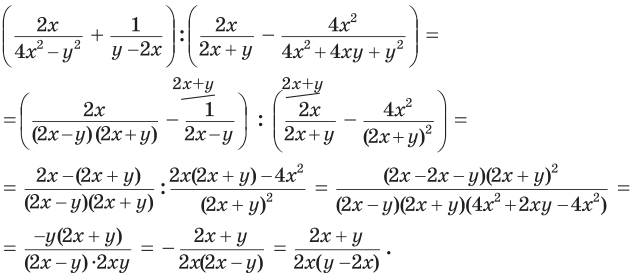
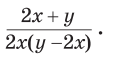
Відповідь:
Поданий у прикладі вираз звели до раціонального дробу
Взагалі, кожний вираз, що містить суму, різницю, добуток та частку раціональних дробів, можна подати у вигляді раціонального дробу.
VI. Засвоєння вмінь
Виконання усних вправ
-
Яка послідовність дій у виразі
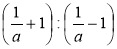 ?
?
-
Прокоментуйте виконання дій у виразі
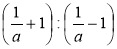 .
.
1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() .
.
Відповідь. ![]() .
.
- Розкладіть на множники вираз:
а) тп – пk; б) т2п – тk; в) 9т2п – 6тk; г) т2 – п2; д) т2 – 1; є) т2 – 4n2;
ж) т3 – 4m; з) т3 + 8; и) m4 – 4m3 + 4m2.
Виконання письмових вправ
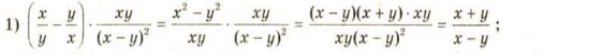
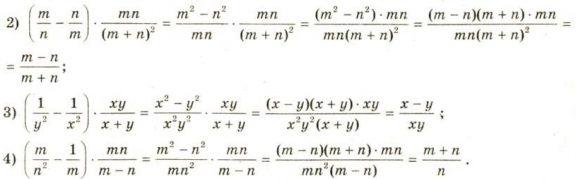
![]()
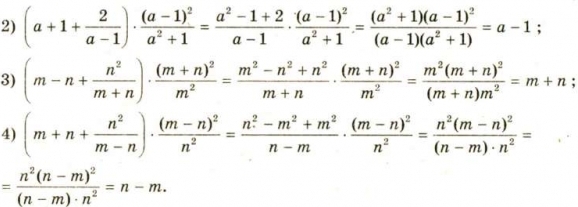

VII. Підсумки уроку
В якому з випадків правильно вибрана послідовність дій із раціональними виразами?
а) 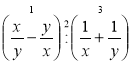 ; б)
; б)  ; в)
; в) 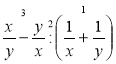 .
.
VIII. Домашнє завдання
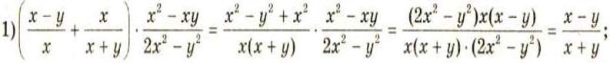


про публікацію авторської розробки
Додати розробку
