Урок "Формули перетворення суми та різниці тригонометричних функцій у добуток"

Тема: Формули перетворення суми та різниці тригонометричних функцій у добуток

Мета: вивчити формули перетворення суми та різниці тригонометричних функцій у добуток; формувати вміння застосовувати їх до перетворення тригонометричних виразів; розвивати логічне мислення учнів, їх пізнавальну активність, ініціативу, культуру математичного мовлення; виховувати наполегливість, старанність, толерантність, комунікабельність.

Тип уроку: вивчення нового матерілу

Обладнання: таблиця «Формули перетворення суми та різниці тригонометричних функцій у добуток», картки із завданнями для роботи у групах та для індивідуальної роботи, дидактична гра «Лото», картки до диктанту «Шифрувальник»

Хід уроку

І. Оргмомент.

Перевірка готовності учнів до уроку. налаштування на роботу.

ІІ. Актуалізація опорних знань.

Інтерактивна вправа « Установити відповідність». Математичне лото (робота в парах)

2.Математичний диктант «Шифрувальник». Обчислити значення виразів та розшифрувати вислів (індивідуальна робота)

1)  2sincos  =

2) cos²sin²  =

3) cos80^ocos20^o + sin80^osin20^o =

4) sin21^o cos9^o + cos21^osin9^o =

5) sin(-60^o) =

6) tg(- 45^o)  =

7) cos(-60^o) =

8) =

9) cos2 + sin ² =

10) (1 – sin) (1 + sin

11) sin² + (1 – cos ² =

12) sin ctg =

« ПОДИХ ІСТОРІЇ»

3. Повідомлення учнів «Подих історії»

Учень 1.Слово «тригонометрія» в перекладі з грецької означає «вимірювання трикутників». Термін «тригонометричні функції» ввів німецький математик Георг Клюгель (1739-1812), який визначив тригонометричні функції як відношення сторін трикутника.

Синус і косинус першими ввели індійські вчені. Подальший розвиток вчення про тригонометричні величини отримало в IX-XV століттях у країнах Середнього і Близького Сходу, де було введено нові тригонометричні величини: тангенс, котангенс, секанс, косеканс та встановлено основні співвідношення між ними.

Цікавим є той факт, що поняття «тангенс» і «котангенс», як і перші таблиці цих величин, з’явились не внаслідок розгляду тригонометричного кола, а із вчення про сонячний годинник.

В другій половині XVIII століття великий внесок у розвиток тригонометрії, як самостійного розділу математики, вніс Ейлер, за походженням швейцарець. Він першим увів відомі означення тригонометричних функцій, почав розглядати функції довільного кута, вивів формули зведення. Велика заслуга Ейлера полягає в тому, що він систематизував тригонометрію.

Учень 2 . Тригонометрія довгий час розвивалась, як частина геометрії, в зв’язку з потребою в астрономів розв’язувати задачі певного виду (передбачення затемнень). Астрономів цікавили співвідношення між сторонами і кутами сферичних трикутників, складених з великих кругів, що лежать на сфері.

Сьогодні тригонометрія розглядається як дисципліна, що вивчає тригонометричні функції та їх застосування,що відіграє важливу роль в геометрії, при вивченні комплексних чисел, при розв’язуванні рівнянь, при вивченні коливальних процесів, при вивченні функцій загального вигляду (наприклад, ряди Фур’є).

Потребують знання тригонометрії природничі науки. Розвиток вчення про коливальні рухи, звукові, світлові, електромагнітні хвилі привів до того, що одним з основних завдань тригонометрії стало вивчення та опис коливальних процесів. Широко використовують тригонометрію у фізиці, хімії.

В останні десятиріччя в зв’язку з швидким розвитком супутникової геодезії впроваджено новий метод створення геодезичних мереж з використанням супутникових радіонавігаційних систем, заснований на законах тригонометрії.

ІІІ. Мотивація навчальної діяльності.

В математиці й техніці досить часто доводиться перетворювати суму або різницю двох тригонометричних функцій на добуток. Питання актуальне при розв’язуванні рівнянь, тому завдання уроку - вивчити формули перетворення та навчитись їх застосовувати.

ІV. Пояснення нового матеріалу .

Учитель наводить доведення формули перетворення суми синусів двох кутів на добуток:

sin(x +у) =sinxcosу +cosxsinу

sin(x -у) =sinxcosу -cosxsinу  
Додамо дані рівняння та зробимо підстановку х + у = ; х – у =  

Маємо,  sin + sin = 2 sincos.

Сума синусів двох кутів дорівнює подвоєному добутку синуса півсуми цих кутів на косинус  їх піврізниці.

Аналогічно отримуємо формули різниці синусів, суми та різниці косинусів. 

sinαsinβ = 2 sincos

Різниця синусів двох кутів дорівнює подвоєному добутку синуса піврізниці цих кутів на косинус їх півсуми.

cos + cos = 2 coscos.

Сума косинусів двох кутів дорівнює подвоєному добутку косинуса півсуми цих кутів на косинус їх піврізниці.

cos-cos =  2 sin  sin .

Різниця косинусів двох кутів дорівнює взятому із знаком «мінус» подвоєному добутку синуса півсуми цих кутів на синус їх піврізниці.

Два учні з високим рівнем математичної освіти виводять самостійно формули суми та різниці тангенсів на дошці.

tg + tg = ;         tgtg = .

V. Застосування вмінь, знань та навичок.

1. Робота в групах під керівництвом учнів-консультантів

І група. Знайти значення виразу:

1.sin 32^о + sin28^о 2 sin30^оcos 2^o= cos 2^o,

2.sin55^о–sin25^о 2 sin15^оcos40^o,

3. cos 52^o + cos18^o  = 2cos35^o cos17^o,

4. cos 78^o – cos18^o  = - 2sin30^o sin48^o  = - cos 48^o,

5.tg2 + tg = = .

ІІ група. Знайти значення виразу (картки з підказками):

1. sin3α + sinα 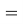2 sincos  =

2. sinβ–sin5β 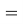2 sincos  =

3. cos 2х+ cos4х  = 2cos   cos  =

4. cosу– cos3у  =  - 2 sinsin =

5. tg2β + tg5β = = =

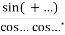2. Самостійне розв’язування прикладу з подальшою перевіркою.

Спростити вираз    .

3. Колективне розв’язання з коментуванням     sin15^о–cos 65^о

4.Виконання диференційованих завдань з підручника ( за необхідністю учитель надає індивідуальні консультації)

Початковий рівень №935( Іст)

Середній рівень - № 935( ІІст)

Достатній рівень №939

Високий рівень №943(3, 4)

VI. Підсумок уроку

Вправа «Мікрофон»:

• Ми повторювали…
• Доводили…
• Вчилися…
• Застосовували…
• Удосконалювали

Виставлення та коментування оцінок консультантами груп

Самооцінювання

Аргументовне оцінювання знань учнів учителем

VIІ. Домашнє завдання.

Мерзляк А.Г. Алгебра і початки аналізу : підруч. для 10 кл. загальноосвіт. навч. закладів : проф.. рівень – Х . :Гімназія, 2010

1. п.43(вивчити формули)
2. Виконати різнорівневі завдання: № 938, 939, 940, 944(5)