Урок. Формули скороченого множення
Про матеріал
В презентації є багато корисної інформації для школярів, яка поглиблює і розширює їхні знання. Перегляд файлу
Зміст слайдів
ppt
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
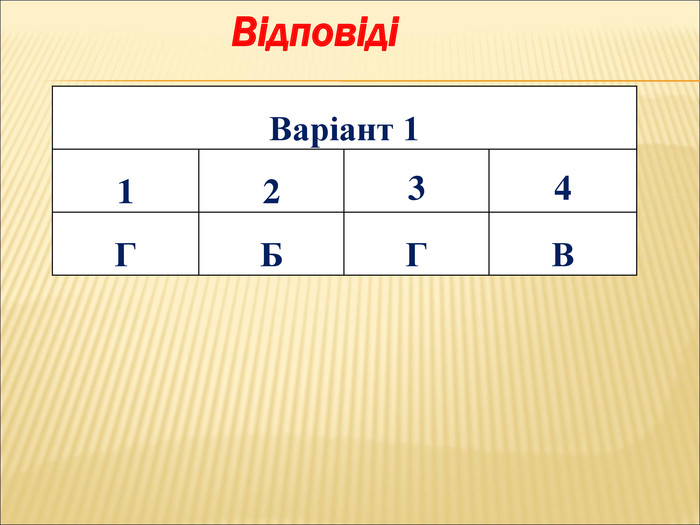
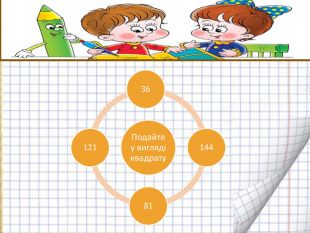
Перетворення многочлена у квадрат суми або різниці двох виразів Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку