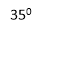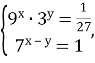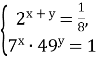Урок геометрії у 11 класі "Піраміди. Правильна піраміда"

Варіант  1

1.(1б) Скільки бічних ребер у чотирикутної призми?

    а) 4;        б) 8;             в) 12;             г) 16.

2.(1б)  Якщо кожне ребро правильної шестикутної призми дорівнює а, то площа її бічної поверхні дорівнює:

а) 2а²; б) 4α²; в) 6a²; r) 8a².

3.(1б)  Якщо ребро куба дорівнює 3 см, то його площа поверхні дорівнює:

а) 9 см²; б) 36 см²; в) 54 см²; г) 27 см².

4.(1б)  Якщо виміри прямокутного паралелепіпеда дорівнюють 8 см, 9 см і 12 см, то його діагональ дорівнює:

а) 12 см; б) 17 см; в) 20 см; г) 29 см.

 5.(1б) Обчисліть площу бічної поверхні прямої призми, основа якої трикутник зі сторонами 10см, 12см і 13см, а бічне ребро дорівнює 8см.

    а) 70см²;   б) 140см²;     в) 210см²;    г)280см².

 6.(1б) Обчисліть площу бічної поверхні прямої призми, основою якої є паралелограм зі сторонами 8см і 22см, а висота призми дорівнює 15см.

   а) 900см²;    б) 450см²;     в) 600см²;    г)2640см².

7.(2б) Точка А належить одній з граней двогранного кута і віддалена від другої грані на 6см. Знайдіть відстань від точки А до ребра двогранного кута, якщо величина цього кута дорівнює 30⁰.

8.(2б) Бічне ребро прямої чотирикутної призми дорівнює 9см. Знайдіть площу повної поверхні призми, якщо її основа – прямокутник, діагональ якого дорівнює 10см, а одна із сторін – 8см.

9.(2б) Основою прямого паралелепіпеда є ромб зі стороною а і тупим кутом . Менша діагональ паралелепіпеда нахилена до площини основи під кутом . Знайдіть площу бічної поверхні паралелепіпеда.

Варіант  2

1.(1б) Скільки  ребер у трикутної призми?

    а) 9;        б) 12;             в) 10;             г) 6.

2.(1б)  Якщо кожне ребро правильної восьмикутної призми дорівнює а, то площа її бічної поверхні дорівнює:

а) 2а²; б) 4а²; в) 6а²; г) 8а².

3.(1б) Якщо поверхня куба дорівнює 24 см², то його ребро дорівнює:

а) 2 см; б) 3 см; в) 4 см; г) 6 см.

4.(1б)  Якщо виміри прямокутного паралелепіпеда дорівнюють 12 см, 16 см і 21 см, то його діагональ дорівнює:

а) 23 см; б) 25 см; в) 27 см; г) 29 см

5.(1б) Обчисліть площу бічної поверхні прямої призми, основа якої чотирикутник зі сторонами 8см, 5см, 12см і 9см, а бічне ребро дорівнює 4см.

    а) 136см²;   б) 68см²;     в) 102см²;    г)140см².

6.(1б) Обчисліть площу бічної поверхні прямої призми, основою якої є ромб зі стороною 6см, а висота призми дорівнює 12см.

   а) 432см²;    б) 72см²;     в) 144см²;    г)288см².

7.(2б) Точка М належить одній з граней двогранного кута і віддалена від його ребра на 4см. Знайдіть відстань від точки М до другої грані кута, якщо величина цього кута дорівнює 45⁰.

8.(2б) Бічне ребро прямої трикутної призми дорівнює 7см. Знайдіть площу повної поверхні призми, якщо її основа – прямокутний трикутник, гіпотенуза якого дорівнює 10см, а один із катетів – 6см.

9.(2б) Основою прямого паралелепіпеда є ромб зі стороною а і тупим кутом . Більша діагональ паралелепіпеда нахилена до площини основи під кутом . Знайдіть площу бічної поверхні паралелепіпеда.

ВАРІАНТ 1

 І частина

1.Знайдіть невідомий кут трапеції:

А)135⁰       Б)35⁰           В)45⁰      Г)визначити неможливо

2. Якщо основи трапеції 5 см і 7 см, то її середня лінія дорівнює…

А)6       Б)12          В)35      Г)визначити неможливо

3.Середні лінії трикутника дорівнюють 3 см, 4,5 см, 5 см, тоді сторони     трикутника дорівнюють…

А) 3 см, 4,5 см, 5 см      Б) 6 см, 9 см, 10 см

В) 5 см, 6,5 см, 7 см     Г)визначити неможливо

4. Знайдіть вписаний кут, якщо центральний в коло кут дорівнює   100°

А)50⁰     Б)100⁰           В)200⁰      Г)визначити неможливо

5. Два кути чотирикутника, вписаного в коло, дорівнюють 80° і 95°. Знайти    два інші кути.

А)100⁰ і 85⁰ Б)120⁰ і 105⁰ В)80⁰ і 95⁰ Г)визначити неможливо

ІІ частина

6. Три сторони, описаної трапеції, взяті послідовно, відносяться, як 2 : 5 : 7.Знайдіть сторони трапеції, якщо її периметр дорівнює 54 см.

7. Знайдіть основи трапеції, якщо вони відносяться як

3 : 5, а середня лінія дорівнює 16 см.

ІІІ частина

8. Діагоналі рівнобічної трапеції є бісектрисами гострих кутів, а основи трапеції  дорівнюють 6 см і 10 см. Знайдіть периметр трапеції.

ВАРІАНТ 2

І частина

1.Знайдіть невідомий кут трапеції:

А)135⁰       Б)35⁰           В)45⁰      Г)визначити неможливо

2. Якщо основи трапеції 6 см і 8 см, то її середня лінія дорівнює…

А)7       Б)14          В)48      Г)визначити неможливо

3.Середні лінії трикутника дорівнюють 3,5 см, 4 см, 6 см, тоді сторони     трикутника дорівнюють…

А) 3,5 см, 4 см, 6 см      Б) 7 см, 8 см, 12 см

В) 5,5 см, 6 см, 8 см     Г)визначити неможливо

4. Знайдіть центральний кут, якщо вписаний в коло кут дорівнює    50°

А)100⁰       Б)50⁰           В)25⁰      Г)визначити неможливо

5. Два кути чотирикутника, вписаного в коло, дорівнюють 100° і 85°. Знайти    два інші кути.

А)80⁰ і 95⁰ Б)100⁰ і 115⁰ В)100⁰ і 85⁰ Г)визначити неможливо

ІІ частина

6. Три сторони, описаної трапеції, взяті послідовно, відносяться, як 2 : 7 : 12.Знайдіть сторони трапеції, якщо її периметр дорівнює 56 см.

7. Знайдіть основи трапеції, якщо одна із них на 8 см більша за іншу, а середня   лінія дорівнює 16 см.

ІІІ частина

8. Діагоналі рівнобічної трапеції є бісектрисами тупих кутів, а основи трапеції дорівнюють 5 см і 9 см. Знайдіть периметр трапеції.

1 варіант

І рівень

1. Знайти х, якщо

        А. 3;   Б. -3;  В. 4;  Г. 1.

  2. Розв’яжіть нерівність

    А) ;   Б)    В) (-Г)

  3. Із наведених нижче функцій показниковою є:

А) ;    Б) ;   В) ;   Г)

4. Обчисліть х+у, якщо (х; у) – розв’язок системи рівнянь  

А) -2;   Б) 2;   В) -2;   Г) -4;   Д) 0.

5. Знайдіть добуток коренів рівняння

А) 10;  Б) -7;  В) 7;  Г) 12;  Д) -10.

ІІІ рівень

6. Визначте найменший цілий розв’язок нерівності

7. Розв’язати рівняння:  

ІV рівень

8. Розв’язати нерівність:

;

2 варіант

І рівень

1. Знайти х, якщо

        А. 3;   Б. -3;  В. 4;  Г. 1.

  2. Розв’яжіть нерівність

    А) ;   Б)    В) (-Г)

  3. Із наведених нижче функцій показниковою є:

А) ;    Б) ;   В) ;   Г) .

4. Обчисліть ху, якщо (х; у) – розв’язок системи рівнянь  

А) 0;   Б) 18;  В) -18;  Г) -28;   Д) -2. 

5. Знайдіть суму коренів рівняння

А) -5;  Б) -3;  В) 15;  Г) 4;  Д) 5.

ІІІ рівень

6. Визначте найменший цілий розв’язок нерівності

7. Розв’яжіть рівняння 

ІV рівень

8. Розв’язати нерівність:

;