Конспект уроку на тему "Об'єм призми"

Методична мета: використання інноваційних технологій на уроках математики

 

Тема:    Об’єми геометричних тіл

 

Урок: № 3

 

Тема уроку:  Об’єм призми

 

Мета уроку: ознайомити учнів із формулою для обчислення об'єму призми, навчити застосовувати її до розв'язання задач, показати зв'язок досліджуваного матеріалу з реальною дійсністю; розвивати інтерес до вивчення предмета; виховувати ерудованість, наполегливість.

 

Методи навчання:

1) Тестового контролю.

 2) Інтерактивні.

 3) Наочні.

 4) Проблемно-пошуковий.

 5) Практичні.

 6) Критичного мислення.

 

Тип уроку: комбінований

 

Міжпредметні зв’язки: історія, технологія приготування їжі.

 

КМЗ: мультимедійна установка, презентація до уроку, тестові завдання, геометричні фігури.

 

ХІД УРОКУ

І. Організаційний момент

Перевірка готовності учнів до уроку Одержання інформації від чергових про відсутніх на уроці.  Налаштування на роботу.

 

ІІ. Перевірка домашнього завдання

   Виконання тестових завдань з теми  «Об’єм паралелепіпеда»  (5 – 10 хв.)

 

ІІІ. Мотивація навчальної діяльності учнів

Сьогодні на уроці, ми будемо  вивчати об'єми многогранників і покажемо важливість теми у вашій професії. А от яка тема сьогоднішнього уроку, ви довідаєтеся після розв'язання кросворда.

 

 

 

 

 

Питання до кросворда

1. Пряма призма, в основі якої лежить правильний многокутник називається …

2. У правильній призмі рівні прямокутники – це бічні ...

3. Два рівних многокутники, що лежать у паралельних площинах називаються …

4. Відрізки, що з'єднують вершини многокутників – це бічні ...

5. Якщо всі грані паралелепіпеда є прямокутниками, то паралелепіпед називається...

6. Як називається переріз тіл обертання площиною, що проходить  через вісь?

7. Тіло, утворене обертанням прямокутника навколо його сторони називається…

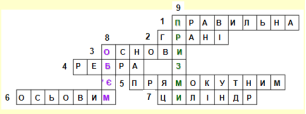8. Геометрична величина.

9. Вид многогранників.

                                  Слайд 1

 

 

 

Прочитайте по вертикалі слова з виділеними буквами, це й буде тема нашого уроку  (об'єм призми)

Повідомляється тема  та мета уроку      Слайд 2 (записується число)

З метою створення ситуації, що допоможе учням усвідоми­ти необхідність вивчення нового матеріалу уроку, можна за­пропонувати їм розв’язати задачу професійного змісту.

Для чого вивчати це поняття?

На практиці часто виникає потреба знати не тільки геометричні фігури та їх основні поняття, а й знати об’єми деяких геометричних тіл.

Створення проблемної ситуації   Слайд 3

Наприклад: У їдальню завезли ящик масла розмірами 50×35×20 см (висота, ширина, довжина) і розрізали його на кубики з ребром - 2,5 см. На яку кількість учнів вистачить масла, якщо на сніданок подають на одного учня  - 1 кубик масла.

Як ви вважаєте, що для вирішення даної ситуації нам необхідно знати?

Після обговорення ситуації, учні доходять висновку, що, для того щоб дати відповідь на запитання задачі, необхідно обчислити об’єм призми та куба.

Відповідь на приклад можна надати швидко, якщо знати формулу, із якою ви ознайомитися сьогодні на уроці. Адже недарма ще французький  письменник Анатоль Франс говорив, що не достатньо знати, необхідно також вміти застосовувати.   Слайд 4

Перед тим як приступити до вивчення нового матеріалу пропоную дещо пригадати.

ІV. Активізація пізнавальної діяльності

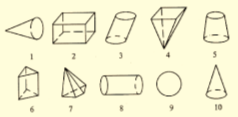1. На якому з малюнків зображено призму?   Слайд 5

 

 

 

 

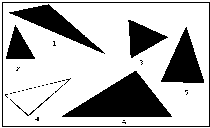2. Який з трикутників є основою правильної трикутної призми?   Слайд 6

 

 

 

 

3. Який з чотирикутників є основою правильної чотирикутної призми? Слайд 7

 

 

 

 

 

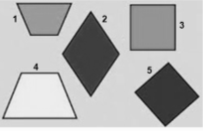
4. Назвіть елементи призми    Слайд 8

 

 

 

 

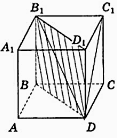
5. Зіставте формули з відповідними поняттями   Слайд 9

 

 

 

 

 

 

 

V. Сприйняття та усвідомлення нового матеріалу. Осмислення і закріплення знань учнів.

     План вивчення теми

1. Історичні відомості.
2. Формула для обчислення об’єму призми.
3. Застосування формули для обчислення об’єму призми.

 

 

 

1. Історичні відомості     Слайд 10

У пам'ятниках вавилонської й давньоєгипетської архітектури зустрічаються такі геометричні фігури, як: куб, паралелепіпед, призма.

Слайд 11 Найважливішою задачею єгипетської й вавилонської геометрії було визначення об'єму різних просторових фігур. Ця задача відповідала необхідності будувати будинки, палаци, храми й інші споруди.

Слайд 12  Об'єми зернових комор у вигляді кубів, призм і циліндрів єгиптяни й вавилоняни, китайці й індіанці обчислювали шляхом множення площі основи  на висоту. Одному древньому Сходові були відомі в основному тільки окремі правила, знайдені досвідченим шляхом, якими користувалися для знаходження об'ємів і площ фігур. Але значно пізніше, коли геометрія сформувалася як наука, був знайдений загальний підхід до обчислення об'ємів многогранників.

 

2. Формула для обчислення об’єму призми.

Слайд 13  Отже, об’єм будь – якої призми дорівнює добутку площі її основи на висоту:

Записи у зошиті:   V = S_осн. ∙ Н.

(щоб знайти площу основи треба знати площі трикутників та чотирикутників, тому що вони є основами призми)

!Треба пам’ятати, що чотирикутна призма називається паралелепіпедом, а якщо вона правильна і пряма, то це – куб. Отже окрім цієї формули для знаходження об’єму призми, можна застосовувати формули: V = a ∙ b ∙ c, та V = a³.

 

3. Застосування формули для обчислення об’єму призми.

      Розв’язування задач

Задача №1   Слайд 14

У кухаря є деко для випікання, яке має форму правильної чотирикутної призми, сторона основи якого дорівнює 25 см, а висота – 7 см. Який об'єм запіканки можна виготовити в даній формі.

Розв'язання:

 V = S_осн. ∙ Н                                     

S_осн = а²                                                         

S_осн = 25² = 625 см²                                                                   

V = 625 · 7 = 1225 cм³

Відповідь:  4375 см³

 

 

Задача №2   Слайд 15

 Коробка із соком має форму чотирикутної призми. Знайдіть її об’єм, якщо сторони її основи дорівнюють 8 см та 10 см, а висота – 35 см. Скільком учням вистачить цього напою, якщо кожен з них вип’є 200 см³ соку?

Розв'язання:

V = S_осн. ∙ Н

S_осн = a · b = 8 · 10 = 80 см² 

V = 80 · 35 = 2800 cм³

2800 : 200 = 14 (учням)

Відповідь:  14 учням

Вирішення проблемного питання

Задача №3    Слайд 16

У їдальню завезли ящик масла розмірами 50×35×20 см (висота, ширина, довжина) і розрізали його на кубики з ребром - 2,5 см. На яку кількість учнів вистачить масла, якщо на сніданок подають на одного учня  - 1 кубик масла.

Розв'язання:

V = S_осн. ∙ Н

S_осн = 35 · 20 = 700 см²

V_ящ. = 700 · 50 = 35000 cм³

V_куб. = 2,5³ = 15,625 (см³)

= = 2240 (учнів)

Відповідь: 2240 учнів  

Перед розв’язанням задачі №4 повторимо величину літра   Слайд 17

 

 

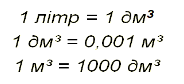
Задача №4   Слайд 18

Електропательня  СЕСМ - 0,2 має об'єм 36 л. Знайти її висоту.

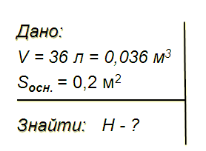Розв'язання:                                                                                    Слайд 19

V = 36л = 0,036 м³, S_осн = 0,2м²

Так як V = S_осн. ∙ Н, то

(м)

Відповідь: 0,18 м

VІ. Рефлексія   Слайд 20

Технологія критичного мислення “Кубик Блума”.

Методика використання:

1. Знадобиться звичайний паперовий куб, на гранях якого написано:
Назви. Чому. Поясни. Подумай. Назви асоціацію. Опиши.

2. Формулюється тема уроку. 

3. Учитель кидає кубик, грань, що випала, вказує на те, якого типу питання слід задати. Зручніше орієнтуватися по слову на грані кубика – з нього і має починатися питання.

Запитання вчителя:

1. Назви

Назви що таке об’єм? Яким символом він позначається? Одиниці вимірювання?

2. Чому

Чому об’єм чотирикутної призми та об’єм паралелепіпеда однакові?

3. Поясни

Ти впевнений, що формула для знаходження об’єму паралелепіпеда та чотирикутної призми однакові?

4. Подумай

Подумай чому буде дорівнювати об’єм призми, якщо її основою є прямокутний трикутник?

5. Назви асоціацію

З чим асоціюється у тебе чотирикутна призма?

6. Опиши

      Опиши з чого складається призма.

VІІ. Підведення підсумків уроку  

Слайд 21 Згадаймо слова французького  письменника Анатоля Франса «Не достатньо знати, необхідно також вміти застосовувати». Справді, ми побачили і в черговий раз переконалися на уроці, що знати формули це не основне, треба вміти їх застосовувати на практиці.

Слайд 22  Працюючи разом, маючи поряд надійних партнерів, ми досягли певного успіху. Але в житті і в навчанні часто для досягнення повного успіху треба вміти працювати без допомоги, повністю самостійно. Тому продовжувати працювати над розв’язанням задач ви будете вдома.

 

VІІІ. Домашнє завдання   Слайд 23 - 24

1. Вивчити формули
2. Розв’язати задачі

Задача№1

У кондитерський цех надійшли ящики для цукерок Гулівер. Чи помістяться в ящик розміром 38 × 29 × 11 см.

а) 200 шт,                                                                             

б) 300 шт.

Розміри однієї цукерки 8  × 3,5  × 2 см.

(з’ясовуємо з учнями, що цукерки мають форму паралелепіпеда, а 8  × 3,5  × 2 см, це його лінійні розміри: висота, ширина, довжина)

Задача №2

Класні кімнати повинні бути розраховані так, щоб на кожного учня припадало не менше 6 м³  повітря. Скільки учнів можна розмістити у нашому кабінеті математики, який має форму прямокутного паралелепіпеда з вимірами 8,8 м, 6,4 м і 3,2 м не порушуючи санітарних норм?

(треба нагадати учням, що кабінет має форму паралелепіпеда, а його розміри це -  висота, ширина, довжина)