Урок геометрії в 10 класі "Піраміда та її елементи"

Урок геометрії ІІ курс         06.02.2018 р.

Тема уроку: Подорож  у світ пірамід.

Мета уроку: Сформувати поняття піраміди, правильної та зрізаної піраміди            та їх елементів. Засвоїти властивості правильних пірамід, формули для обчислення площі повної та бічної поверхні піраміди. Розвивати творчу та пізнавальну активність учнів, уміння робити висновки на основі даних, отриманих під час досліджень. Розглянути піраміду не тільки як геометричну фігуру, а й різні аспекти її використання. Виховувати в учнів бажання до самовдосконалення.

Вид уроку: Інтерактивний.

Обладнання: Мультимедійний проектор, екран, моделі пірамід.

Девіз уроку: Все на землі боїться часу, і тільки час боїться пірамід.

ХІД УРОКУ

1. Актуалізація опорних знань.

Давайте згадаємо наше дитинство, ми часто грались з іграшкою «Пірамідка». Також ми зустрічаємо у повсякденні предмети які мають вигляд піраміди.                             Слайд 2

Також багато будівель у Світі збудовані у вигляді піраміди. 7 чудо Світу це Піраміди!

Слайд 3

А з яких пласких фігур складається піраміда: трикутник, чотирикутник, многокутник.

2. Оголошення теми нового матеріалу.

Тема «Піраміда, та її елементи».

Пірамідою називається многогранник, одна грань якого довільний многокутник (основа піраміди), а решта граней являють собою трикутники які мають спільну вершину (вершина піраміди).                                                                                                                                             Слайд 4

Розглунимо основні елементи піраміди: Вершини, Ребра, Грані, Бічна поверхня, Площина основи, Висота, Апофема.

За якими формулами можна обчислити площу основи?    Слайд 5-7

Всі піраміди відрізняються одна від одної є прямі, похилі, скошені і т.д.

Але є серед них одні єдині неповторні ПРАВИЛЬНІ.     Слайд 8

Піраміда називається правильною – якщо в основі піраміди лежить правильний многокутник, а всі ребра (і ребра основи, і бічні ребра) рівні.

Висота правильної піраміди падає перпендикулярно в центр кола, описаного навколо основи, і всі апофеми бічних граней рівні.

Як обчислюються площі правильних фігур: трикутника, квадрата, шестикутника?

Слайд 9-10

А сьогодні нас цікавить таке запитання. Як знайти площу бічної поверхні піраміди?

Звернимось до підручника. Ст. 224    п. 29   Теорема 7.

Площа бічної поверхні піраміди дорівнює добутку півпериметра її площі основи на довжину апофеми бічної грані піраміди

 

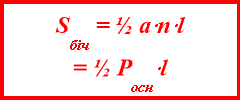
                                                                      Слайд 11

 

 

 

 

Щоб знайти площу повної поверхні піраміди необхідно, до  площі бічної поверхні піраміди додати площу основи

 

 

 

                                                                 Слайд 12

Піраміду можна розрізати площинками: паралельною,  перпендикулярною, під кутом.

Слайд 13

Щоб виготовити піраміду необхідно знати розгортку піраміди ось Вам представлено розгортки різноманітних пірамід.                                                                                                   Слайд 14

Піраміди в грошах, в медицині, в жіночій фігурі, в прапорах держав.  Слайд 15-18

3. Закріплення знань і умінь отриманих на уроці
4. Розв’язування вправ

 Відома піраміда Хеопса в Єгипті – правильна чотирикутна піраміда, висота якої дорівнює 147м, а площа основи – 5,3 га. Знайдіть міру двогранного кута при ребрі її основи і кут нахилу до площини основи її бічного ребра.                                           Слайд 19

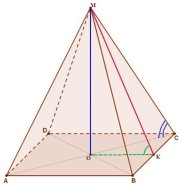
Дано: МABCD – піраміда;

АВСD-Квадрат;

SАВСD=5,3га=5300 м²;

МО=147 м;

________________

Знайти : Двогранний кут нахилу апофеми до висоти піраміди.

 

Розв’язок

5,3 га=5300 м²;

АВ=√5300=230 м;

То ОК=1/2АВ =115м;

З трикутника МОК, tgМОК=ОМ/ОК=147/115 ≈ 1,2783 ≈ 52^о

З трикутника АВС за теоремою Піфагора АС²=2АВ², (2ОС)²=2АВ2,ОС=АВ/√2=230/√2;

З трикутника МОС tgМОС=МО/ОС=147√2/230 ≈ 0,9038 ≈ 42^о.

Виконання учнями тестів (відповіді «так» і «ні»):      

- Чи існує піраміда, яка має 125 ребер?

- Чи існує піраміда, яка має 125 граней?

- Чи  може піраміда мати дві бічні грані, перпендикулярні до основи?

- Якщо в піраміді бічні ребра утворюють з висотою рівні кути, чи                                      проектується  її вершина в центр кола, вписаного в основу?         

- Якщо висоти всіх бічних граней, проведені із вершини піраміди, рівні, чи буде основа висоти центром кола, вписаного в основу?

- Якщо бічні ребра піраміди рівні і в основі лежить тупокутній трикутник, чи буде основа висоти лежати поза основою?

-  Якщо бічні ребра піраміди рівні і в основі лежить прямокутний трикутник, чи буде основа висоти лежати всередині основи піраміди?

- Чи може піраміда мати три бічні грані, перпендикулярні до площини основи?

- Якщо одна з бічних граней піраміди перпендикулярна до основи, чи збігається висота піраміди з висотою однієї грані?

-  Чи може піраміда мати два бічні ребра, перпендикулярні до основи?

-  Чи існує піраміда, яка має 18 плоских кутів?

- Чи можуть бути рівними бічні ребра піраміди, якщо в її основі лежить трапеція?

             Слайд 20-21

5. Підсумки уроку, виставлення оцінок( тести, робота в групах)

Відповідь до тесту 1-в,2-б,3-а,4-а,5-б,

                                 6-б,7-б,8-а,9-б,10-а.

6. Домашнє завдання. п.29,творче завдання «Чому піраміди зображені на банкнотах США та України?» №№941,943,945