Алгебра. 7 клас                                                             Дата:__________

 

Вчитель математики:    Кузь Вікторія Петрівна

 

Тема:           Графічний спосіб розв’язування систем лінійних рівнянь

 

Мета: освітня: розвивати в учнів вміння розв’язувати системи лінійних рівнянь графічним способом; розвиваюча: розвивати вміння вільно висловлюватися з теми, відпрацьовувати вміння говорити коротко, але по суті й переконливо, розвивати навички спілкування в групах; виховна: виховувати активність, увагу, інтерес до нових знань і прагнення їх набути

 

Тип уроку: Комбінований урок

 

Обладнання: мультимедійний проектор, презентація в PowerPоіnt,  роздатковий матеріал, таблиця «Розташування графіків рівнянь системи»

 

 

 

 

 

 

 

Хід уроку:

Слайд 1

 

 

I. Організаційний момент

Перевірити готовність учнів до уроку: наявність на столах зошитів та письмового приладдя, готовність дошки. 

 

ІІ. Перевірка домашнього завдання

На початку уроку зібрати зошити для перевірки. Відповісти на запитання учнів, які виникли під час виконання домашнього завдання.

ІІІ. Актуалізація опорних знань

Фронтальне опитування «Дай відповідь»:

1.     Які рівняння називаються лінійними рівняннями з двома змінними?

2.     Що означає запис M(x; y)?

3.     Що є графіком рівняння першого степеня з двома змінними?

4.     У якому випадку говорять, що дані рівняння утворюють систему?                

Як записують систему рівнянь?

5.     Що називають розв’язком системи рівнянь з двома змінними?

6.     Що означає розв’язати систему рівнянь з двома змінними?

 

Слайд 2

 

 

Виконання вправ: І група:

1.     (1) Заповніть пропуск так, щоб пара (2,5; ...) задовольняла рівняння 2𝑥−𝑦=0. Відповідь. (2,5; 5)

2.     (3) Знайдіть координати точки перетину графіка рівняння  𝑥−3𝑦=3 з віссю Ох. Відповідь. (3; 0)

 

ІІ група:

1.     (2) Заповніть пропуск так, щоб пара (…; -3) задовольняла рівняння 3𝑥−2𝑦=0. Відповідь. (-2; -3)

2.     (6) Побудувати графік лінійного рівняння з двома змінними  𝑥−𝑦=4.

 

ІІІ група:

1.        (4) Знайдіть координати точки перетину графіка рівняння 2𝑦−4𝑥=−4 з            віссю Оу.

Відповідь. (0; -2)

2.        (5) Побудувати графік лінійного рівняння з двома змінними  3𝑥+2𝑦=6.

 

 

                                                               Слайд 3 (початок)                                 Слайд 3 (кінець)

                                    

 

 

Історична довідка (доповідь учня):

 

 

                                                                                    Слайд 4

 

 

31 березня у світі святкувалася річниця від дня народження цього великого філософа і математика. З ім’ям Декарта пов’язане відкриття методу координат. Ми креслимо графіки, за їх допомогою розв’язуємо задачі. Він один з перших запропонував графічний спосіб розв’язування рівнянь. Г.П. Бевз так написав про його відкриття: 

Він числа і фігури об’єднав,

А лінії й рівняння ототожнив, І людству метод надпотужний дав −Такий, що знає нині його кожний.

Він з геометрією алгебру здружив,

Обох подвоївши можливості і силу. Достойно геній шану заслужив −Творець нового методу і стилю.

 

 

 

ІV. Повідомлення теми мети і завдань уроку. Мотивація навчальної діяльності

Розв’язувати системи лінійних рівнянь можна трьома способами. Сьогодні ми з вами познайомимося з тим способом саме який і був запропонований Рене Декартом. Отже темою нашого уроку є: «Графічний спосіб розв’язування систем лінійних рівнянь».

На уроці ми будемо вчитися розв’язувати системи лінійних рівнянь з двома змінними графічно.

Слайд 5

 

 

V. Формування вмінь і навичок учнів

Поетапне розв’язування вправи колективно:

Системи лінійних рівнянь з двома змінними можна розв'язувати графічним способом. Для цього треба:

 

Слайд 6

 

Розв’язання:

 

x	5	1
y	0	2

x	0	1
y	0	-3

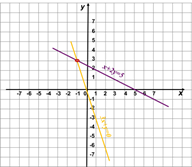𝟑𝒙+𝒚=𝟎                                  𝒙+𝟐𝒚=𝟓

 

 

 

Відповідь. (-1; 3)

 

самостійно:

Слайд 7

 

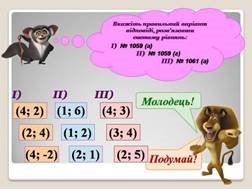
Відповідь: І) (4; 2),   робота в групах:	ІІ) (1; 2),	ІІІ) (3; 4) Слайд 8

Порада учням:
ІІ) 𝒙+𝟐𝒚=𝟑			𝟐𝒙+𝟒𝒚=𝟔

x	3	1
y	0	1

x	1	3
y	1	0

 

ІІІ)		𝟑𝒙+𝟒𝒚=𝟐				𝟗𝒙+𝟏𝟐𝒚=−𝟔
	x -2 2 y 2 -1				x -2 2 y 1 -2

 

розгляд схеми «Розташування графіків рівнянь системи»:

 

На площині можливі три випадки

взаємного розташування двох прямих –                                                                                           графіків рівнянь системи:

1) прямі перетинаються; 2) прямі співпадають; 3) прямі паралельні.

 

 

 

VІ. Домашнє завдання

1.   Вивчити конспект

2.   с. 231 «Виконаємо разом» № 2.

3.   Виконати  А) № 1060, Б) № 1060, 1062.

 

                                                               Слайд 9                                                            Слайд 10

                          

 

VІІ. Підведення підсумків уроку

1. Інтерактивна технологія «Мікрофон»

-         Тема нашого уроку…

-         Скільки є способів розв’язування систем лінійних рівнянь? Які?

-         Що потрібно зробити для того, щоб розв’язати систему графічним способом?

 

2.     Виставлення оцінок

 

3.     Закінчую урок такими словами англійського математика Лу́иса Джо́эля Морделла: «Ніхто не піде далеко в математиці і не стане справжнім математиком, якщо не матиме деяких необхідних рис. У ньому повинні жити Віра, Надія і Допитливість, і найважливіша з цих рис − Допитливість. Він повинен раз у раз запитувати себе: чому, як і коли − і це мусить стати головним рушієм, що приводить його в дію.»