Урок інформатики у 10 класі Тема: Кодування і передавання повідомлень

Урок № 2                                                     І – 10 клас                              Дата:

 

Тема. Кодування та декодування повідомлень.

 

Мета:  формувати знання одиниць вимірювання обсягу двійкового коду; розуміння відмінностей у принципах кодування інформації різного виду; уміння пояснювати принципи передавання повідомлень технічними каналами зв’язку; уміння визначати обсяг двійкового коду; розвивати ключові компетентності: математичну, компетентності у галузі природничих наук, техніки і технологій, інформаційно-комунікаційну.

Обладнання та наочність: мультимедійна презентація, комп'ютер, підручник, картки.

Тип уроку: засвоєння нових знань і умінь.

Хід уроку

І. ОРГАНІЗАЦІЙНИЙ МОМЕНТ

 

II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

• Що таке біт? ( мінімальна одиниця кількості інформації, яка дорівнює одному двійковому розряду, який може бути рівним одному з двох значень/станів (0 або 1)..)
• Що таке байт? (одиниця вимірювання обсягу даних. Найменша адресована одиниця пам'яті ЕОМ. Містить 8 бітів.)
• Двійковий код? (Кодування повідомлень із використанням двох сигналів називається двійковим. Набір даних, отриманий у результаті двійкового кодування, називається двійковим кодом.

 

Відтвори записку:

1 ___ (___байт) = 210 байт = 1024 байт;

1 Мб (мегабайт) = 210 Кб = _____ байт = 1 048 576 байт;

1 Гб (гігабайт) = 210 Мб = 220 Кб = ____ байт;

1 Тб (терабайт) = 210 Гб = 220 Мб = 230 Кб = ____ байт.

 

 

1 Кб (кілобайт) = 210 байт = 1024 байт;

1 Мб (мегабайт) = 210 Кб = 220 байт = 1 048 576 байт;

1 Гб (гігабайт) = 210 Мб = 220 Кб = 230 байт;

1 Тб (терабайт) = 210 Гб = 220 Мб = 230 Кб = 240 байт.

 

III. Мотивація навчальної діяльності.

Ви знаєте, що дані бувають текстові, графічні, звукові. Нам потрібно з’ясувати, як кодуються у комп’ютері дані різних видів, і навчитись розраховувати обсяг цих даних.

IV.  Вивчення нового матеріалу.

 

Кодування графічних даних.

Комп’ютерну графіку можна розподілити на растрову, векторну, фрактальну, тривимірну (рис. 2.1, а–г).

 

 

 

 

 

 

 

 

У файлі растрового зображення закодовано кольори всіх його пікселів.

 

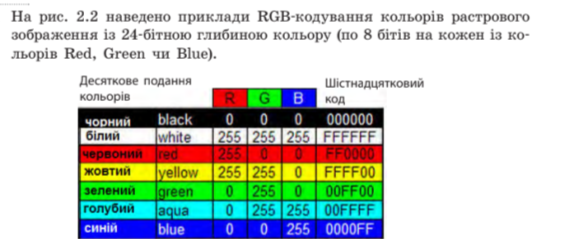
 Глибина кольору – це кількість бітів, які використовуються для кодування кольору пікселя растрового зображення.

 

 

 

 

 

 

 

 

 

 

 

 

 

У векторному зображенні кодуються властивості його графічних примітивів: форма (пряма, крива), товщина, колір, накреслення (пунктирна, суцільна), заливка тощо.

У тривимірній (3D) графіці моделюються просторові об’єкти, завдяки чому виникає можливість розглядати їх під будь-яким кутом, змінювати розташування, освітлення, властивості матеріалів тощо. Під час створення таких об’єктів поєднуються растровий і векторний способи формування зображень, а код тривимірного зображення доповнюється інформацією про розміри об’єктів, можливості їх перетворення, проекції тощо і зале-

жить від особливостей 3D-редактора.

У фрактальній графіці базовими елементами є математичні формули. Файл фрактального зображення зберігає закодовані рівняння, за якими воно будується.

 

Кодування звукових даних.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

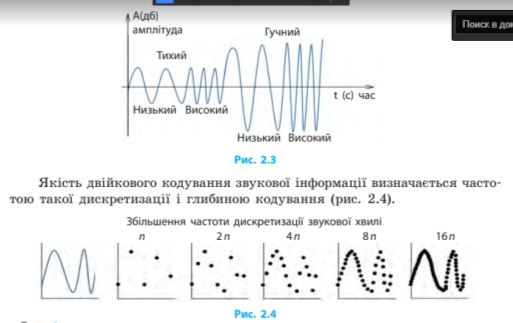
Частота дискретизації — це кількість вимірювань рівня сигналу за одиницю часу.

Одиницею вимірювання частоти дискретизації є 1 герц.

 

Глибина кодування — це кількість бітів, необхідна для кодування одного значення рівня сигналу.

 

Обсяг двійкового коду

Для розрахунку обсягу двійкового коду Q, потрібного для кодування даних, використовують формулу Q=k⋅i, де k — кількість елементарних порцій даних; i — кількість двійкових розрядів, потрібних для кодування елементарної порції даних (символу, пікселя та ін.).

 

Задача на розрахунок обсягу текстових даних

Який обсяг двійкового коду потрібен для кодування повідомлення:

Привіт, світе! за системою Unicode версії UTF-16?

Розв’язання

 

i=16 (UTF-16 використовує 16-бітове кодування); k=14 (кількість сим-

волів, враховуючи пробіли і розділові знаки).

 

Тоді обсяг двійкового коду: Q=k⋅i=14⋅16=224 біти = 28 байтів.

 

Задача на розрахунок обсягу графічних даних

 

Який обсяг двійкового коду потрібен для кодування растрового зображення розміром 100 на 100 пікселів при 24-бітовій глибині кольору?

 

Розв’язання

i = 24 (глибина кольору); k = ⋅ 100 100 10 000 = (кількість пікселів).

Тоді обсяг двійкового коду:

Q k = ⋅i = ⋅ 10 000 24 240 = 000 біти (або 240 000/8/1024 ≈ 29,3 Кбайта).

 

Задача на розрахунок обсягу звукових даних

 

Визначити обсяг аудіофайла тривалістю 1 хв із частотою дискретизації 24 КГц і глибиною кодування 8 бітів.

 

Розв’язання

t = 601 хв = 60 c; h=24 КГцh = 24 000 Гц; i = 8 ; k=h. t;

Q=k. Q h = ⋅t i⋅ =i 24 000⋅ ⋅ 60 8 1= 1520 000 бітів

(або 11 520 000/8/1 048 576 ≈ 1,4 Mбайта).

Мінімально можлива кількість двійкових розрядів, які потрібні для кодування елементарної порції даних (символу, пікселя та ін.), може бути розрахована за співвідношенням 2i n, де n — кількість символів, кольорів тощо.

 

Задача на розрахунок кількості двійкових розрядів

Якою є найменша кількість бітів для кодування десяткових цифр?

Розв’язання

n =10 (кількість десяткових цифр); 2i n; 2 10 i  . Звідси i = 4 біти.

Передавання повідомлень

Як ви знаєте, інформація передається за допомогою повідомлень.

А повідомлення передаються від джерела до приймача каналами зв’язку.

Під час розмови по телефону звукові сигнали (голос) перетворюються

(кодуються) на електромагнітні, які мережею передаються до співрозмовника й знову перетворюються (декодуються) на звукові сигнали.

 

На практиці до корисного сигналу майже завжди додаються супутні перешкоджаючі сигнали, які називають шумом.

Телефонній розмові можуть заважати гучна музика, розмова інших людей, завивання вітру, гуркіт автомобілів, тріск у слухавці тощо.

 

Шум — це різного роду перешкоди, які спотворюють корисний сигнал і призводять до спотворення інформації.

 

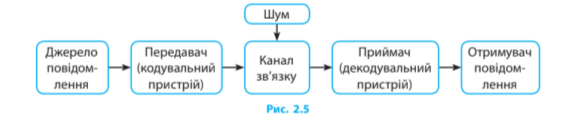Таким чином, узагальнена схема передавання повідомлень технічними каналами зв’язку (схема Шеннона) із урахуванням шуму має такий вигляд (рис. 2.5).

 

 

 

 

Пропускна здатність каналу зв’язку

 

Пропускна здатність каналу — це максимальна швидкість передавання даних каналами зв’язку.

 

Що ж впливає на пропускну здатність інформаційного каналу зв’язку?

 

Здавалося б, пропускна здатність каналу зв’язку, наприклад, дротових ліній, обмежена лише швидкістю поширення електромагнітних коливань у провіднику, а отже, практично є необмеженою. Але це не так, бо накладання шуму (перешкоджаючих сигналів) може призвести до спотворення одного або кількох корисних бітів. У разі збільшення швидкості

 

передавання даних шум устигає вразити більше корисних бітів.

Отже, чим вища швидкість передавання даних за певного рівня шуму, тим вищим є рівень помилок. Тобто шум є причиною обмеження пропускної здатності інформаційного каналу. Математичну залежність пропускної здатності каналу від відносних потужностей корисного сигналу і шуму установив К. Шеннон.

 

V. Осмислення набутих знань.

Вправа 2

1. Запишіть, який обсяг двійкового коду (у байтах) при 16-бітовому кодуванні має повідомлення Інформаційний простір України.

2. Скільки мегабайтів потрібно для збереження файла чорно-білого растрового зображення розміром, який дорівнює розміру (в пікселях) екрана вашого монітора? Пам’ятайте, що пікселі чорно-білого

 

зображення кодуються одним бітом: білий — 1, чорний — 0.

3. Скільки часу триватиме прослуховування аудіофайла обсягом

1 кбайт із бітрейтом 124 кбіт/с?

 

Примітка. Бітрейт — це кількість аудіоданих, переданих каналами зв’язку за одиницю часу (біт/с). Розраховується бітрейт (B) так:

 

B h = ⋅ I, де h — частота дискретизації, I — глибина кодування.

4. Розрахуйте, яка найменша кількість бітів потрібна для кодування літер української абетки та поясніть, чому для кодування символів зазвичай використовують 8-бітову систему, а не 7- чи 6-бітову.

 

VI. Підсумки уроку.

1. Як кодується символьна інформація?

2. Які особливості кодування растрових зображень; векторних?

3. Які параметри впливають на якість оцифрованого звуку?

4. Як розраховується обсяг двійкового коду закодованих даних?

5. Наведіть приклади впливу шуму на передавання даних

6. Назвіть елементи схеми Шеннона.

 

VIІ. Домашнє завдання.

Опрацювати § 2.

Виконати Комп’ютерне тестування тестове завдання 2.