Урок "Математичний маятник. Період коливань математичного маятника"

Математичний маятник.

Період коливань математичного маятника

11 клас

Квадріціус Сергій Якович, учитель фізики Ст

Мета: Знаннєвий компонент: сформувати поняття «маятник», розглянути види маятників, які існують та яка поміж ними різниця; вивести формулу  періоду коливань математичного маятника; застосувати формулу для розв’язування задач;

Діяльнісний компонент: продовжувати формувати в учнів уміння спостерігати фізичні явища, користуватися приладами, самостійно визначати мету діяльності, організовувати навчальну діяльність у взаємодії, працювати з підручником, порівнювати, встановлювати зв’язки між новими та засвоєними знаннями, застосовувати аналогію як засіб засвоєння нового; розвивати інтелектуальні та творчі здібності, мислення, увагу, пам’ять, робити висновки, аналізувати;

Ціннісний компонент: сприяти розвитку наукового світогляду на прикладі коливальних процесів; виховувати пізнавальний інтерес, такі якості як вміння співпрацювати з іншими учнями, комунікативність та розвивати грамотну мовну культуру.

Тип уроку:   вивчення нового матеріалу і первинне закріплення.

Обладнання:

1. Моделі математичного та фізичного маятників.
2. Нитки різної довжини.
3. Секундомір (електронний годинник).
4. Підручники з фізики.
5. Мультимедійна дошка.
6. Відеофрагмент «Маятник Фуко в Ульмському соборі (Мюнстер, Німеччина)».

Демонстрації:

• Коливальний рух фізичного тіла навколо осі обертання.
• обертання математичного маятника.

 

План-схема уроку

 

№ п/п	Етап уроку	Час, хв.	Форми і методи діяльності вчителя	Результат діяльності
1	Організаційний	1	Розподіл учителем учнів класу на групи.	Створення дослідницьких груп.
2	Актуалізація опорних знань	5	Гра «Встановимо відповідність». Гра «Відновити означення»	Актуалізація опорних знань.
3	Мотивація навчальної діяльності	3	Бесіда з учнями. Перегляд відеофрагменту «Маятник Фуко в Ульмському соборі (Мюнстер, Німеччина)». Демонстрація різних маятників.	Активізація та розвиток логічного мислення, підготовка учнів до сприйняття нового матеріалу. Створення сприятливого психоемоційного клімату.
4	Формулювання теми та визначення мети уроку	2	Допомагає сформулювати тему та мету уроку.	Формулювання учнями теми та мети уроку
5	Вивчення нового навчального матеріалу	15	Допомагає учням скласти план дослідження та провести саме дослідження відповідно до цього плану	Засвоєння навчального матеріалу. Вироблення практичних умінь. Розвиток слухової, зорової, комбінованої пам’яті. Розвиток аналітичного та дедуктивного мислення
6	Рефлексія знань	15	Учні біля дошки розв’язують задачі Тестування.	Закріплення знань.
7	Підсумок уроку	3	Інтерактивна вправа «Мої очікування»	Підведення підсумків уроку, оцінювання діяльності учнів
8	Домашнє завдання	2	Завдання репродуктивного характеру.	Засвоєння теми та підготовка до наступного уроку

 

Геніальні відкриття – це 99 % праці та 1 % таланту.

 

Томас Едісон.

Хід уроку

І. Організаційний момент

Я, Квадріціус Сергій Якович, вчитель Станіславської школи проведу урок фізики під девізом: «Геніальні відкриття – це 99 % праці та 1 % таланту».

 Але працювати на уроці необхідно злагодженою командою, тому необхідно познайомитися.

Знайомство розпочинається з підписування бейджиків.

Вчитель створює в класі доброзичливу, творчу, робочу атмосферу. Наголошує на тому, що оцінювання за урок буде відбуватися за допомогою смайликів, які видаватимуться за запитання по темі, відповіді на поставлені запитання, досліди та за іншу творчу і пізнавальну активність.

Особливість цього уроку полягає в тому, що на кожній другій парті знаходиться набір для дослідження: нитки різної довжини, тягарці, підручники та зошити. Четверо учнів знаходяться біля кожного набору цих приладів (учні двох сусідніх парт гуртуються в одну групу).

 

ІІ. Актуалізація опорних знань

Спочатку повторимо матеріал, який вивчався вами раніше.

Гра «Встановимо відповідність»

1. Що називають коливаннями?
   • рухи, які повторюються через однакові проміжки часу.
2. Що називають маятником?
   • це тверде тіло, яке здійснює коливання навколо нерухомої точки.
3. Які маятники називають фізичними?
   • маятники, які коливаються під впливом сили тяжіння  Землі.
4. Які маятники називають пружинними?
   • маятники, в яких тіло коливається під впливом сили пружності.

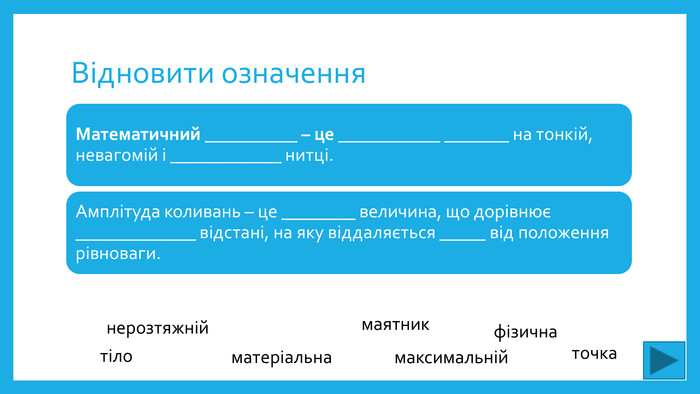
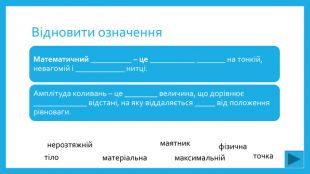
Гра «Відновити означення»

1. Який маятник називають математичним?
   • матеріальна точка на тонкій, невагомій і нерозтяжній нитці.
2. Дати визначення амплітуди коливань
   • це фізична величина, що дорівнює максимальній відстані, на яку віддаляється тіло від положення рівноваги.

 

ІІІ. Мотивація навчальної діяльності

Вчитель говорить про те, що видів нерівномірного руху є багато. Окрім уже відомого нам  обертального руху,  ми вивчимо ще один вид нерівномірного руху. Потім вчитель показує відеофрагмент «Маятник Фуко в Ульмському соборі (Мюнстер, Німеччина)».

Невеликий відступ про Жана Бернара Леона Фуко.

Опісля  показує приклади коливань різних маятників, запитує в учнів, що є спільного у всіх цих рухах та що їх різнить із обертальним рухом;  просить сформулювати тему сьогоднішнього уроку та якої мети ми повинні досягнути.

 

ІV. Формулювання теми та визначення мети уроку.

Учні записують у зошити тему  уроку. Пишеться на дошці:

Математичний маятник. Період коливань математичного маятника

 

V. Вивчення нового матеріалу.

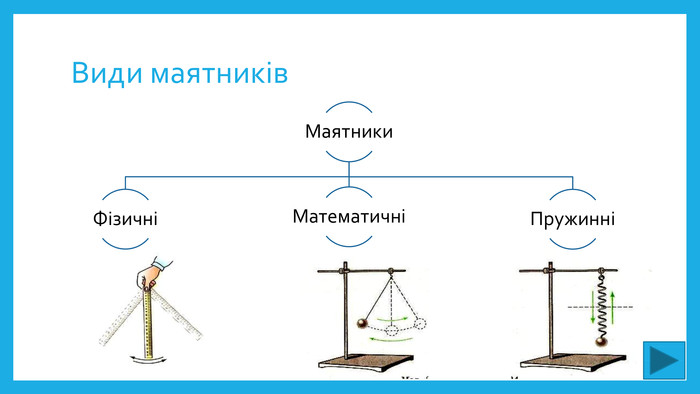
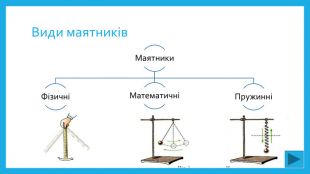
Які види маятників існують? В чому їх подібність та відмінність?

Вчитель знайомить з різними видами маятника і наголошує, що розпочнемо вивчення теми з математичного маятника.

Формулювання означення математичного маятника (методом почергового складання речення, а потім - навпаки)

Математичний маятник -  це фізична модель, яка являє собою матеріальну точку, що підвішена на невагомій і нерозтяжній нитці та здійснює коливання під дією сили тяжіння.

Для визначення закономірностей руху математичного маятника створимо та розглянемо його модель. Для цього візьмемо кульку невеликого розміру (вона слугуватиме матеріальною точкою), підвісимо її. Змусимо маятник коливатися в одній площині.

Виведемо емпіричним шляхом формулу періоду коливань математичного маятника.

Коливальна система – точкове тіло на нерозтяжній невагомій нитці.

Нехтуємо:

• масою нитки (значно менша маси тіла);
• розмірами тіла (значно менші розмірів нитки);
• розтягом нитки;
• тертям об повітря.

На відхилену від положення рівноваги в крайнє положення кульку діє рівнодійна сил тяжіння F_т = mg і сили F_пр пружності (натягу) нитки і напрямлена в положення рівноваги.

Відпущена кулька рухається в положення рівноваги. Знову ж швидкість і прискорення напрямлені в одну сторону, швидкість зростає.

В положенні рівноваги сили скомпенсовані,  швидкість максимальна. Внаслідок інертності рух продовжуються до відхилення в інше крайнє положення.

Зупинившись на мить, кулька почне рух в протилежну сторону – рух повториться.

Визначимо період коливань маятника.

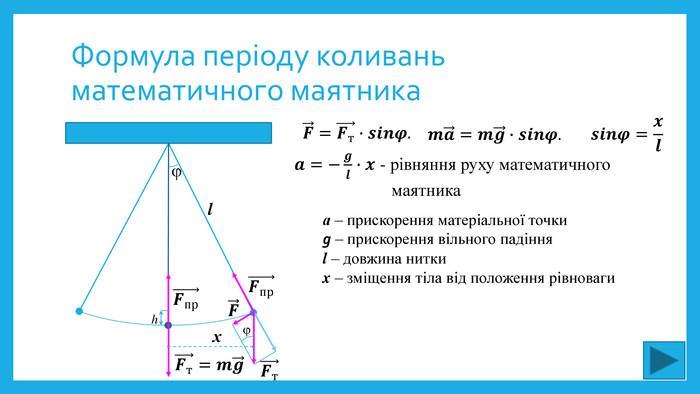
Виконаємо рисунок на заготовці. Клеємо заготовку в зошит.          

Так як довжина нитки маятника набагато більша за величину відхилення, величину h прийнято вважати близькою до нуля.

Вісь ОХ направлена по дотичній до траєкторії руху,   вісь OY  - вздовж лінії дії сили натягу нитки.

Так як h = 0, то вздовж осі OY тіло не рухається.

або

Так як прямокутні трикутники (показує) подібні, тому що відповідні кути рівні, а отже сторони пропорційні.

Знайдемо синус кута  з більшого прямокутного трикутника (показує), у якому гіпотенуза – довжина нитки l, катет, що лежить проти кута , дорівнює зміщенню (амплітуді) маятника від положення рівноваги х. А синус гострого кута прямокутного трикутника дорівнює відношенню протилежного катета до гіпотенузи. Маємо:

Для рівняння коливань математичного маятника одержуємо:

Це знову ж гармонічне коливання, яке можна записати у вигляді: 

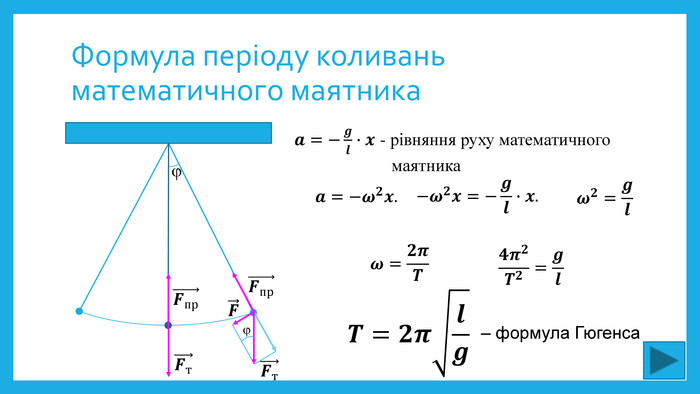
Відповідно для циклічної частоти маємо:

Проте , що одержуємо формулу періоду коливань математичного маятника

           

Звернімо увагу від чого залежить і від чого не залежить період коливань математичного маятника, у яких одиницях вимірюється.

Період коливань не залежить від маси тіла чи амплітуди коливань, а визначається лише довжиною підвісу та прискоренням вільного падіння у даному місці.

За формулою бачимо, що період математичного маятника прямо пропорційний квадратному кореню з l.

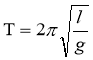, де l – довжина маятника (особливість маятника), і
g – прискорення земного тяжіння (особливість гравітаційного поля Землі).

 

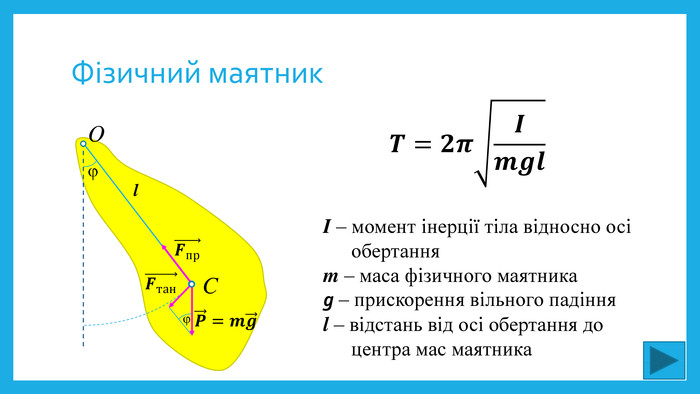
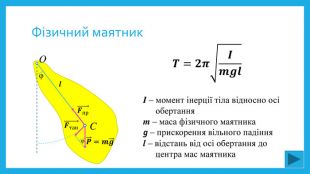
Крім математичного маятника сьогодні на уроці розглянемо і фізичний маятник.

За готовим рисунком підручника розберемо модель фізичного маятника. (Пояснення)

А зараз відпочинимо і подивимось де використовуються маятники (слайди 14-16).

Маятники Фуко на території України

• Переяслав-Хмельницький, Музей пізнання світогляду та освоєння космосу
• Київ, бібліотека Київського політехнічного інституту
• Харків, Харківський національний університет
• Харків, Харківський планетарій
• Ужгород, Ужгородський національний університет
• Львів, Церква Пресвятої Євхаристії
• Луцьк, СРК «Adrenalin City»
• Одеса, Музей цікавих наук

 

VІ. Закріплення знань

     Учні біля дошки розв’язують задачі.

Задача 1. Маятник Фуко Київської політехніки має висоту 22 м. Визначити період його вільних коливань.

 

Дано:

l = 22 м

g = 9,8 м/с²

 

 

Т - ?

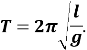
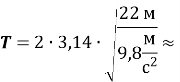
 9,4 с.

Відповідь: 9,4 с.

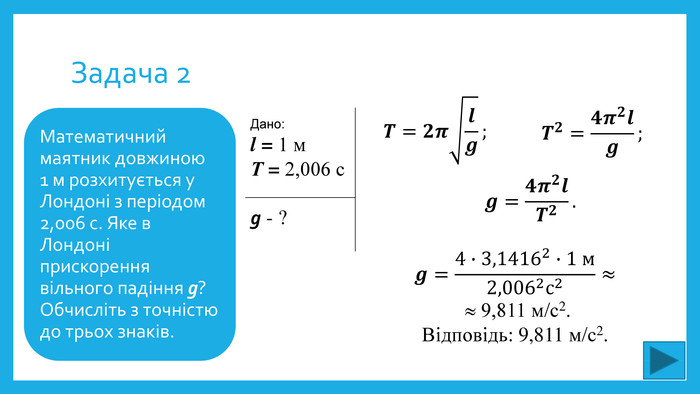
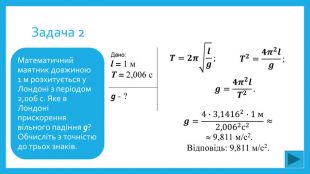
Задача 2. Математичний маятник довжиною 1 м розхитується у Лондоні з періодом 2,006 с. Яке в Лондоні прискорення вільного падіння g? Обчисліть з точністю до трьох знаків.

 

 

Дано:

l = 1 м

Т = 2,006 с

 

 

 

g - ?

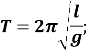
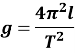
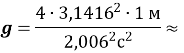
  9,811 м/с².

Відповідь: 9,811 м/с².

Завдання 3. Математичний маятник довжиною 1 м (з попередньої задачі) в Лондоні висить нерухомо. Який тепер період коливання?

Т = 2,006 с.

 

Тестування.

За QR-кодом:

 

VІІ. Підсумок уроку

Інтерактивна вправа «Мої очікування»

Учні діляться враженнями, чи справдились їх очікування. Отримують солодощі.

 

 

     VІІІ. Домашнє завдання:

 

1. §

2. Вправа