Урок на тему "Формули подвійного аргументу"

Тема. Формули подвійного аргументу. Розв’язання вправ.

Мета: домогтися засвоєння тригонометричних формул подвійного аргументу; закріпити знання цих формул під час розв’язання вправ; розвивати вміння порівнювати, самостійно мислити; виховувати інтерес до математики, удосконалювати навички самоконтролю.

Тип урок: засвоєння нових знань, формування вмінь.

Обладнання: конспект, підручник Мерзляк А.Г. Алгебра і початки аналізу 10 клас , картки самоконтролю

;

Хід уроку

I. Організаційний етап.

Налаштувати учнів на продуктивну роботу на уроці, роздати картки самоконтролю

II. Перевірка домашнього завдання( по зошитах)

III. Формулювання мети і завдань уроку.

На попередньому уроці ми вивчили тригонометричні формули додавання. Ці формули мають багато наслідків. Тригонометричні формули подвійного аргументу є наслідком формул додавання. Тобто тригонометричні формули додавання дозволяють виразити , , через тригонометричні функції кута . Тож наша мета – це вивчення формул подвійного аргументу.

IV. Актуалізація опорних знань.

Повторення формул додавання.

Виконати усно( за кожне завдання 0,5 балів)

1) ;

2) ;

3) ;

4) .

V. Засвоєння знань.

План

1. Вивчення формул синуса подвійного аргументу.

2. Вивчення формул косинуса подвійного аргументу.

3. Вивчення формул тангенса подвійного аргументу.

Формули, які виражають тригонометричні функції аргументу через тригонометричні функції аргументу , називаються формулами подвійного аргументу.

1) Запишемо формулу для синуса суми: ; Покладемо , отримаємо: ;

2) Аналогічно для наступних функцій:

; ;

Виразимо із тригонометричної одиниці і підставимо у нашу формулу: ;

Тепер виразимо і підставимо у формулу: .

3) Для тангенса: ; ;

Формули для синуса і косинуса виконуються для будь-яких значень аргументу, а формула тангенса подвійного аргументу виконується тільки для тих значень аргументу , для яких визначені і , тобто , і , .

VI. Закріплення нового матеріалу.

1) Виразіть через функції вдвічі меншого аргументу( 1 бал за правильно виконане завдання)

1);№ 13.1(1)

2;№13.1(2)

3)№13.1(4)

2) Спростіть вираз( робота в парах)( 3 бали )

1. ;
2. ;
3. ;
4. ;
5. ;
6. ;

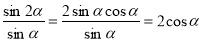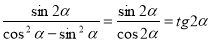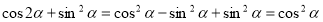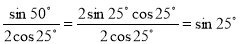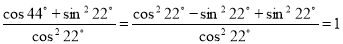3) Обчисліть: (3 бали)

1. ;
2. ;
3. ;
4. ;
5. ;
6. .

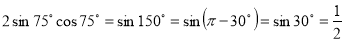4) Знайдіть , якщо і .(1 бал)

; ; ; ;

.

5) Спростіть вираз: (1 бал)

.

7) Довести, що .( додаткове завдання)

VII. Підбиття підсумків уроку.

VIII. Домашнє завдання.

п.13, вивчити формули, №13.10, №13.14, «13.21.