Тема: Основна властивість дробу. Скорочення дробу.

                       Мета: повторити основну властивість дробу та її застосування до скорочення дробів та зведення до нового знаменника, вчити учнів застосувати цей матеріал до розв’язування завдань.

                     Тип уроку: повторення

Хід уроку

I. Організаційний момент.

II. Актуалізація опорних знань, вмінь і навичок  учнів.

1.               Що показує чисельник дробу? (Це число, яке показує кількість взятих долей від цілого).
2.               Що показує знаменник дробу? (Це число, яке показує, на скільки рівних частин поділено певне ціле).

Правильно, а тепер розглянемо таку задачу:

На один з пароплавів навантажили партію фруктів. Команда ... за дорученням перевантажила на свій корабель третю частину від всієї партії, а команда ... — п’яту. Запишіть отриманні дроби у ваші морські журнали, в яких ви вже встигли записати сьогоднішнє число і Класна робота.

Отже, які ви отримали дроби? ().

Придумайте кожен ще по 3 приклади звичайних дробів і запишіть їх поряд з попереднім дробом, й тоді хтось з ваших обох команд прочитає їх. (діти зачитують свої приклади).

Я почула, що хтось з вас назвав неправильний дріб. Що ж ми називаємо неправильним дробом? (Дріб, у якого чисельник більший або рівний за знаменник, називається неправильним дробом).

А як перетворити дріб у неправильний? Як називається це число?

(дробове число або мішаний дріб).

Дробова частина мішаного числа може бути неправильним дробом, наприклад , тоді можна виділити в дробовій частині цілу частину і представити мішане число так, щоб дробова частина стала правильним дробом.

.

Аналогічні дії зробіть з числами (перша команда) та (друга команда).

1) ;

2) .

З ряду чисел, які ви бачите на робочій таблиці, назвіть правильні й неправильні дроби, мішані числа. Це робимо по черзі: один учень з першої команди, інший з другої.

Ряд чисел:

(Правильні дроби: . Неправильні дроби: . Мішані числа: ).

III. Мотивація навчальної діяльності учнів.

IV. Повідомлення теми, мети і завдань уроку.

V. Сприймання і й попереднє усвідомлення учнями нового матеріалу.

Отже, виділіть таку замітку, яка і буде основною властивістю дробу:

Якщо чисельник і знаменик дробу помножити або поділити на одне й те саме натуральне число, то дістанемо дріб, що дорівнює даному.

1.                 Острів навичок надіслав нам такий лист, в якому його мешканці просять вас пояснити їм, чому правильні рівності:

.

2.                 Назвіть кілька дробів, що дорівнюють дробу 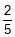. Чому?

().

3.                 Правильно, але мешканцям острову Навичок можливо ще не досить зрозуміло, як замінити дроби, які записані на дошці, рівними їм дробами зі знамеником 50. Допоможемо їм?

Дроби, що записані на дошці:.

З обох команд виходять 2-а учасники виконувати це завдання:

VI. Осмислення об’єктивних зв’язків і відношень, у тому матеріалі, що вивчається.

Далі читаю лист:

Губернаторові острова подарували кавун масою 10 кг 200 г. маси кавуна він віддав дітям, а — з’їв разом з дружиною. Знайти, скільки з’їв губернатор з дружиною і скільки дав дітям, порівняти ці маси.

Розв’язання:

Перш за все переведемо кілограми в грами. Хтось прокоментує:

10 кг 200 г = 10200 г.

г

г

Отже, ми бачимо, що вони з’їли порівну, то що ми можемо сказати про дроби і ? Чому вони рівні?

(І чисельник і знаменик дробу можна домножити на 2 і отримати дріб, який за основною властивістю дробу буде дорівнювати дробу ).

VII. Узагальнення та систематизація знань.

       Давайте ще раз повторимо основну властивість дробу. В кінці листа губернатор пропонує зобразити нам на координатному промені числа, які показують можливі шляхи 2-х кораблів в разі виникнення шторму.

Викораставши основну властивість дробу, інколи можна замінити один дріб іншим, який дорівнює йому, але з меншим чисельником і знаменником.     Наприклад, якщо чисельник і знаменник дробу поділити на їх спільний дільник 11, то дістанемо дріб , який за основною властивістю дробу буде рівний дробу . ().

      Отож, запишемо і виділемо правило входження в порт “Скорочення дробу ”:

Ділення чисельника і знаменника дробу на їх спільний дільник відмінний від одиниці, називається  скороченням дробу.

Найбільшим числом, на яке можна скоротити дріб, є найбільший спільний дільник чисельника і знаменника.

  А зараз, хто швидше з команд скоротить дроби і виділить їх цілі частини? Як саме робити, показано на опорній схемі з прикладами.

       Приклади для розв’язання:

.

()

  Ми бачимо останій дріб() скоротити не можна. Такий дріб називається нескоротним. Чисельник і знаменник нескоротного дробу взаємнопрості числа.

Наведіть приклади нескоротних дробів. (Учні з кожної команди по черзі наводять приклади).

Так, обійшовши скелю, ми з вами потрапили на острів “Зведення дробу до нового знаменника”.

Використавши основну властивість дробу, ми дріб записали із знаменником 100. Для цього чисельник і знаменник дробу помножили на 10. ().

Цей дріб можна замінити дробом зі знаменником 30, помноживши його чисельник і знаменник на 3: .

Нехай дріб треба звести до дробу зі знаменником 120. Спочатку треба дізнатися, на яке натуральне число треба помножити 10, щоб отримати 120 (якщо таке число існує). Для цього треба число 120 поділити на 10: . Тоді .

В цьому прикладі число 12 називають додатковим множником.

VIII. Підведення підсумків уроку.

IX. Повідомлення домашнього завдання.