Урок-подорож "Додавання та віднімання дробів з однаковими знаменниками"

Тема: Додавання та віднімання звичайних дробів з однаковими знаменниками

Мета:  

дидактична: узагальнити і систематизувати знання, вміння і навички учнів по темі: «Звичайні дроби. Додавання та віднімання звичайних дробів з однаковими знаменниками»; перевірити як учні засвоїли тему, їх вміння застосовувати набуті знання у практичній діяльності;             

розвивальна: розвивати логічне, раціональне та критичне мислення, уяву, кругозір, формувати вміння співпрацювати під час виконання групових завдань;             

виховна: виховувати спостережливість, охайність ведення записів, працьовитість, організованість, вміння знаходити вихід із скрутних ситуацій.

«Без знання дробів ніхто не може визнавати, що знає математику»

Цицерон

Тип уроку: узагальнення та систематизації

Хід уроку

І. Організаційний момент

Всі сідайте тихо, діти!

Домовляймось – не шуміти,

Працювати час настав.

Тож і ми часу не гаємо,

Наш урок розпочинаємо!

Для початку пригадаємо вислів великого мислителя Цицерона «Без знання дробів ніхто не може визнавати, що знає математику». Саме цей вислів стане епіграфом нашого уроку.

Сьогодні ми з Вами вирушаємо у незвичайну подорож по Математичному океану. Ось перед вами карта цього океану (карта, на якій вказано маршрут подорожі від порту «Старт» до порту «Фініш»)

Всі зайняли місця відповідно до придбаних квитків. Підпишіть робочі зошити, в яких ви сьогодні будете працювати та виберіть смайлик, що відповідає вашому настрою.

ІІ. Актуалізація опорних знань

    Щоб вирушити в подорож, треба підготувати корабель. Для цього потрібні нам  теоретичні знання.

Усне опитування. Вправа «Мікрофон»

1. Що показує знаменник звичайного дробу?
2. Що показує чисельник  звичайного дробу?
3. Який дріб називається правильним?
4. Який дріб називається неправильним?
5. Як порівняти дроби з однаковими знаменниками?
6. Як порівняти дроби з різними знаменниками?
7. Навести приклади мішаних чисел.
8. Як перетворити мішане число у неправильний дріб і навпаки?
9. Як додати або відняти дроби з однаковими знаменниками?
10. Яки дріб дорівнює 1?
11. Який дріб більший (менший) за одиницю?

ІІІ. Мотивація навчальної діяльності.

 Формулювання теми, мети і завдань уроку

    Подорожувати Математичним  океаном  нам буде допомагати тема сьогоднішнього уроку: «Звичайні дроби. Додавання та віднімання звичайних дробів з однаковими знаменниками». Протягом подорожі ми з вами узагальнимо і систематизуємо знання по даній темі та перевіримо вміння  застосовувати їх у практичній діяльності.

Отже, основним завданням уроку є не просто подолання маршруту від порту «Старт» до порту «Фініш», але й повторення  вивченого.

Ну а працювати ми будемо за девізом: «Не соромно не знати, а дуже соромно не хотіти знати!»

ІV. Розв’язування задач і вправ

А тепер, рушаймо!  Через певну відстань розміщені зупинки, де ми повинні зупинитися і почерпнути щось нове від подорожі.

Дорога до першої зупинки займе певний час, щоб його скоротити, люди, зазвичай, у дорозі або читають, або розмовляють, спілкуються, заводячи нові знайомства. Давайте і ми з Вами трохи відволічемось, а саме –  пригадаємо,  якими правилами ми користуємося при додаванні та відніманні дробів з однаковими знаменниками?

А ось і перша зупинка нашої подорожі – «Усна лічба».

На цій зупинці ми повторимо правила усної лічби, розв’язавши завдання, записані на дошці.

1. +;
2. ;
3. ;
4. ;
5. ;
6. +;
7. .

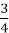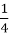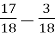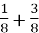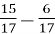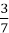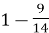         Із завданнями ми справилися, можемо рухатися далі. Під час руху розв’яжемо декілька логічних задач.

☻  Качка, стоячи на одній нозі, важить 2 кг. Скільки вона буде важити,

      якщо стане на другу ногу? ( 2 кг)

☻  Боцман старший за юнгу на 10 років. На скільки років він буде

      старший за юнгу через 5 років? (на 10 років)

О, ми  заговорилися і мало не пропустили зупинку. А це мис «Рівняйлівка». Тут ми з Вами повинні показати, які ми фахівці у розв’язуванні рівнянь:

Необхідно розв’язати рівняння:

                      

                    

 

Увага! Ми наближаємось до «Бухти задач ». Тут розташоване рибальське селище. На березі ми зустріли рибалок, які попросили нас допомогти їм у розв’язуванні задач:

Задачі від  рибаків:

1. За перший день рибалки зловили 40 кг риби, за другий  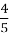– маси першого дня, а за третій - 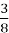маси другого дня. Яка маса спійманої риби за три дні?
2. Бабуся вирішила  виділити  під   тюльпани 3/20 саду,  під  піони - 4/20,

 під хризантеми  - 6/20,  під орхідеї - 2/20,  під троянди - 7/20.  Чи   зможе   вона реалізувати  свій  план?

Всі завдання, які були поставлені перед нами на цій зупинці ми виконали, тепер можемо вирушати далі.

На горизонті ми бачимо, як з’являється острів «Квітковий

Робота в групах

Всі ви любите квіти? Давайте кожен із вас назве свою улюблену квітку, а потім побачимо чи співпала ваша улюблена квітка із назвою тих квітів, які ростуть на острові. От і добре, всі ви назвали різні квіти. А щоб дізнатися назву квітки вам потрібно виконати дії  записані на пелюстках, та розмісти їх у порядку зростання .

 

 

 

Рухаємось до наступної зупинки порт «Обчислювальний».

Робота в парах № 1046

1-2 – перша група

3-4 – друга група

5-6- третя група

 

  На горизонті з’явився острів «Історичний»

(інформація про появу математичного дробу)

Історія появи математичного дробу

Мабуть кожному з вас буде цікаво дізнатися про те, як і коли виникли дроби? І якщо з натуральними числа більш менш відомо, що вони виникли в результаті того, що людині потрібно було рахувати предмети, лічити кількість тварин та вимірювати довжини площі, об’єми.

Але не в усіх випадках в результаті вимірювань виходили натуральні числа, а найчастіше діставалися якісь частини величини.

 Коли первісна людина з полювання приносила здобич у свою печеру, то їй потрібно було її розділити, а без дробового поділу це зробити було неможливо. Вполювавши двох буйволів, потрібно було цю здобич поділити на чотирьох мисливців. Отак, завдяки потребі в неповних величинах і виникло поняття дробу. Тому історія виникнення дробів ведеться майже з самого початку розвитку людства.

Історичні знахідки свідчать про те, що єгиптяни уміли оперувати дробами більш ніж чотири тисячі років тому. Зрозуміло що в ті часи у людини не було потрібних математичних знань та й загальноприйнятого позначення дробів людина в той час ще не знала, тому у кожній країні використовували свої позначки дробів. Єгиптяни в ті далекі часи застосовували одиничні дроби, які зображали, ставлячи крапку над знаменником.

Трохи пізніше, приблизно понад 2500 років тому, в своїх обчислення почали використовувати дроби і греки. В той час вони вже вміли користуватися як одиничними дробами, так дробами, які мали загальний вигляд.

Люди в Київській Русі дробам дали назву часток, а потім їх стали називати ламаними числами. А ось подивіться які назви мали найпоширеніші дроби на Русі:

 

 

Наша подорож по Математичному океані підходить до завершення, оскільки ми прибуваємо до порту «Фініш». Але…

Ой, іще, мабуть не все,

Ось дивіться перед вами,

Хтось писав тут на піску

Нам задачу ось таку.

Та водою позмивало

Цифр у прикладах чимало

Швидше ж бо часу не гайте

Цифри в приклади вставляйте.

;  2) .

 

V.  Підсумок уроку

      Подорож Математичним океаном завершилась. Скажіть, які математичні знання ви застосовували під час нашої мандрівки океаном?

  Дякую Вам, учасники подорожі. Ви гарно впоралися  із завданнями і показали, що можете їх застосовувати на практиці.

А на завершення приводжу вислів відомого російського письменника      Л. Толстого.

Діти, як ви думаєте: що важливіше – що ви про себе думаєте чи що про вас думають інші люди?

Один з відомих письменників, Лев Толстой,  сказав, що людину можна оцінювати дробом, чисельник якого становить те хороше, що вона думає про себе сама, а знаменник -  те хороше, що про цю людину думають інші. То ж бажаю вам,щоб дріб у кожного з вас був завжди правильним.

Оцінювання учнів.

VІ. Домашнє завдання

Повторити параграф 26, розв’язати № 1049, 1103,1117 - повторення