Урок "Призма. Паралелепіпед. Площа поверхні паралелепіпеда"

 

 

Міністерство освіти і науки України

ДНЗ «ВПУ №2 м. Херсона»

 

 

 

 

 

Предмет: геометрія

Професія: «Столяр будівельний, монтажник ГКК»

 

 

 

 

План – конспект уроку

 

Тема уроку «Призма. Паралелепіпед. Площа поверхні паралелепіпеда»

 

 

 

 

 

 

Розробила і провела:                                                                

Степаненко Л.В.

 

 

 

 

 

 

 

 

 

 

Херсон

 

 

Дата проведення ________    Група ________

 

Тема уроку: "Призма. Паралелепіпед. Площа поверхні                                                 паралелепіпеда."                                        

Мета уроку:

 

 

-       Навчальна (дидактична)

 Сформувати поняття площ повної та бічної поверхонь паралелепіпеда; домогтися засвоєння формул;

застосування набутих знань при розв’язуванні задач  теоретичного і практичного характеру  у тісному зв’язку даного учбового матеріалу з життям і майбутньою професією.

-         Розвиваюча

Розвиток самостійного логічного мислення, умінь і навичок практичного застосування одержаних знань; удосконалення досвіду колективної роботи у команді для підвищення успішності та відповідальності; розвиток здібностей пошукового характеру.

Розвиток логічного мислення, просторового уявлення. Усвідомлення необхідності отримання математичних знань  для розвитку особистості, поповнення інтелектуального багажу і розширення кругозору людини.

-         Виховна

Формування елементів колективізму при розв’язанні спільних задач практичного характеру. Виховання взаємоповаги, доброзичливості між учнями і викладачем. Виховання відповідальності, працелюбності, чесності, принциповості у відношенні до себе і до всіх членів колективу групи.

Тип уроку:

Урок  застосування  знань, формування  вмінь і навичок учнів.

Форма проведення уроку: урок –практикум  ( з елементами  змагання між командами)

Методи навчання, прийоми:

Інтерактивні прийоми, групова та індивідуальна робота учнів, самостійна робота, робота з таблицями та опорними конспектами, проблемні питання, практична робота, елементи самоконтролю.

Основні терміни і поняття:

Призма, паралелепіпед, куб, площа поверхні, основа, грань, ребро,висота, вершина…

Міжпредметні зв’язки:

Спецтехнологія, алгебра, креслення, історія.

Програмно-методичне забезпечення уроку:

Мультимедійна дошка, комп’ютери, презентації Microsoft PowerPoint, стенди, таблиці, картки, моделі тіл, опорні конспекти, плакати, зразки моделей столярних виробів з професії.

 

Епіграф уроку:  «Ніколи ще до нашого часу ми не жили в такий геометричний період.  Навколишній світ – це світ геометрії».

                                                                                              Ле Корбюзье                                      

Девіз уроку:

                           «Натхнення  потрібне в геометрії, як і в поезії». 

                                                                            

                                                                                          

Методи навчання:

1. Тестового контролю.

2. Пізнавальні ігри.

3. Лекція.

4. Демонстраційні.

5. Практичні методи.

 

ХІД УРОКУ

 

 І. Організаційний момент

Перевірка готовності учнів до уроку, налаштування на роботу.

 

 ІІ . Формулювання мети й завдань уроку. Мотивація навчальної діяльності учнів

Як сказав видатний французький архітектор Ле Корбюзьє:

«Я думаю, ніколи ще до нашого часу ми не жили в такий геометричний період. Навколишній світ – це світ геометрії».

І, справді, світ, в якому ми живемо, наповнений геометрією предметів, речей, творінням природи і людини. Геометрія виявляється скрізь, де потрібно визначити форми і розміри. Архітектору, інженеру, будівельнику – всім необхідна геометрична уява.

Після закінчення училища ви поповните лави представників однієї з самих гуманних і мирних професій, ставши столярами, а отже – будівельниками. Ви будете робити свій вагомий внесок у будівництво як важливих споруд громадського призначення, так і житла для людей. І, звичайно, воно повинно бути красивим, зручним і теплим. (Фото проектів арх. споруд-Херсон)

Але без знань математики і без вміння їх використовувати на практиці, звичайно, сучасних споруд не побудуєш.

Сьогодні на уроці ми продовжимо вивчення теми «Многогранники» і, звичайно, будемо застосовувати набуті знання при розв’язуванні задач, не забуваючи, звичайно, про тісний зв’язок геометрії з вашою майбутньою професією.

Повідомляється тема  та мета уроку.

(Відео роботи у столярній майстерні)

 

 

ІІІ. Перевірка домашнього завдання

Виконання тестових завдань (на повторення призми):

 

Додаток1(всі разом-варіант1, кожна підгрупа-варіант 2)

 

ІV. Актуалізація навчального матеріалу

Виконання інтерактивних вправ

 

• «Без теорії немає практики»

(Закінчити речення)

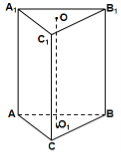
1. Відрізки, які сполучають відповідні вершини призми називаються …
2. Основи призми …
3. Основи призми лежать у …
4. Поверхня призми складається з …
5. Висотою призми називається відстань між площинами …
6. Відрізок, який сполучає дві вершини призми,що не належать одній грані, називається …
7. Призма називається прямою, якщо її  бічні ребра …
8. Пряма призма називається правильною, якщо її основи є …

 

• Бліцопитування

(Дайте відповідь на запитання)

1. Скільки бічних ребер має чотирикутна призма?
2. Скільки ребер основ має трикутна призма?
3. Скільки граней має трикутна призма?
4. Скільки бічних граней має п’ятикутна призма?
5. Скільки всього ребер має п’ятикутна призма?

Відповіді: 4, 6, 5, 5, 15.

 

• Встановити логічні пари:

1.   Бічне ребро	а.               АВ
2.   Висота	б.              А1А
3.   Ребро основи	в.              ОО1
4.   Основа	г.        СС1В1В
5.   Бічна грань	д.             АВС
6.   Бічна поверхня прямої                                     призми	є.                       S = Sбіч.+2Sосн.
7.   Повна поверхня призми	ж.                            S=P∙ℓ

Відповіді: 1-б, 2-в, 3-а, 4-д, 5-г, 6-ж, 7-є.

 

V. Засвоєння знань

Подивіться на речі навколо себе. Що ви бачите, які геометричні фігури та тіла? Більшість речей, які ви бачите, мають форму або геометричної фігури, або поєднання геометричних тіл: куба, паралелепіпеда, кулі, частини кулі, циліндра, призми, тощо.

(Демонстрація слайдів із зображенням речей та споруд, що мають форму геометричних просторових фігур).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(Учням роздаються картки – схеми за якими вони роблять опорний конспект, додаток 2)

 

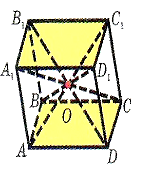
Означення: Паралелепіпедом називається призма, в основі якої лежить паралелограм.

 

Властивості:

1.   У паралелепіпеда всі грані паралелограми.
2.   У паралелепіпеда протилежні грані паралельні і рівні.
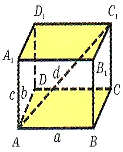
3.   Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться навпіл.(О – середина діагоналей, див. мал..).

 

 

Означення: Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом.

 

 

Властивості:

1.     У прямокутного паралелепіпеда всі грані – прямокутники.
2.     У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його лінійних розмірів, або вимірів (висота, довжина і ширина).

 

 

 

 

 

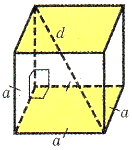
Означення: Кубом називається прямокутний паралелепіпед, у якого всі ребра рівні.

 

Властивість: У куба всі грані – квадрати.

 

+

 

 

 

 

VI. Формування вмінь і відпрацювання навичок

 

Задача 1  ( практичного характеру)

 

Викладач: Хочу запропонувати вам цікаву практичну роботу на обчислення площі бічної поверхні прямокутного паралелепіпеда.  Кожна пара учнів кожної команди одержує міні-модель (всі моделі різної величини). Необхідно знайти  площу, зробивши відповідні заміри.

 

Учні працюють парами і через зазначений час віддають аркуші з розрахунками. Після цього на м/дошці висвітлюються вірні результати для самоперевірки.

 

Номер призми	Розміри (см)	(см кв.)
1	H=…,  а=…,б=…
2	H=
3	H=
4	H=
5	H=
6	H=
7	H=
8	H=
9	H=
10	H=
11	H=
12	H=
13	H=
14	H=

 

 

 

 

 

Задача 2  ( практичного характеру)

 

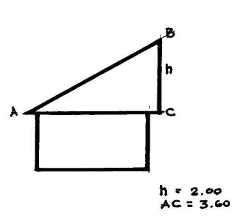
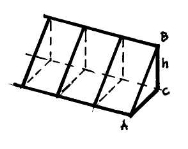
 Скільки листів гіпсокартону(розмір одного листа 2м х 1,2м) потрібно для облицювання внутрішньої бічної поверхні мансардного поверху житлової будівлі, якщо довжина покрівлі:

-І ком.:12м;

-ІІком.:10м;

-ІІІком.:8м.

 

(На екрані фрагмент покрівлі з відповідними значеннями)-Дод.3

 

Представник кожної команди дає відповідь на запитання задачі:

Відповідь І: 31 лист.

(Розв.:  АВ=12,96+4=16,96(кв.м);  Sбічн.1=4,12 х 12=49,44(кв.м);  Sбічн.2=2 х   х 12=24(кв.м); );  Sбічн.1+Sбічн.2=49,44+24=73,44(кв.м);
Площа листа: 2 х1,2=2,4(кв.м);  кількість листів: 73,44:2,4=30,6(31 лист.) )

 

Відповідь ІІ: 26 лист.

(Розв.:  Sбічн.1=4,12 х 10=41,2(кв.м);  Sбічн.2=2 х 10=20(кв.м); Sбічн.1+Sбічн.2=41,2+20=61,2(кв.м);  кількість листів:61,2:2,4=25,5(26 лист.))

 

Відповідь ІІІ: 21 лист.

(Розв.:  Sбічн.1=4,12 х 8=32,96(кв.м);  Sбічн.2=2 х 8=16(кв.м); Sбічн.1+Sбічн.2=32,96+16=48,96(кв.м);  кількість листів:48,96:2,4=20,4(21 лист.))

 

 

Задача 3

 

 Основою прямокутного паралелепіпеда є квадрат зі стороною см. Діагональ бічної грані утворює з площиною основи кут . Знайти площу повної поверхні паралелепіпеда.

 

(Розв.: Sосн.=108кв.см;  Н=6см; Sбічн.= х4 х 6=144(кв.см); Sпов.=108х х 2 + 144=216+244,8=460,8(кв.см) )

 

 

 

 

VII. Домашнє завдання

1. Вивчити зміст понять, розглянутих на уроці і записати їх у зошит.  
2.  Розв.  задачу:

  Діагональ правильного паралелепіпеда дорівнює 9 см, а висота – 1см. Обчисліть площу повної поверхні паралелепіпеда

 

VІІІ. Підсумки уроку. Рефлексія.

Ще раз пригадаємо слова видатного французького архітектора Ле Корбюзьє: «Я думаю, ніколи ще до нашого часу ми не жили в такий геометричний період. Навколишній світ – це світ геометрії».

Справді, ми побачили і в черговий раз переконалися на уроці, що все що нас оточує має геометричну форму, що  без геометрії ми не можемо обійтися і її треба вивчати.

 

Продовжити фрази:

- "на уроці я дізнався …

- "мені сьогодні сподобалось …

- "свою роботу на уроці я оцінюю …

(Викладач оцінює роботу команд і відзначає кращих учнів)

 

Викладач:

Я дякую за урок і сподіваюсь, що математика завжди допомагатиме вам у житті та у майбутній професії.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 1

ТЕСТ І варіант

1. На якому з рисунків зображено призму?

 

 

 

 

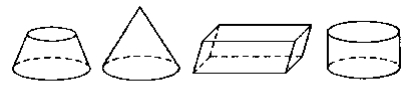
                А.               Б.               В.                Г.

 

2. У п’ятикутній призмі кількість бічних граней:

     А. 7  Б. 5   В. 15    Г. 10

 

3. У прямій призмі бічні грані …

А. Прямокутники   Б. Паралелограми   

    В. Трапеції    Г. Інша відповідь

 

4. У трикутній призмі всього граней є …

    А. 6  Б. 5   В. 7   Г. 8

5. На малюнку зображено куб АВСDA₁B₁C₁D₁. Бічним ребром цього куба є …

 

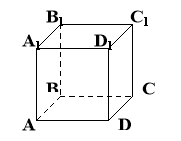
А. АВ Б.D₁C₁  

B.C₁C  Г. ВС

 

 

 

6. У чотирикутній призмі бічних ребер є …

А. 4   Б. 8   В. 12    Г. 16

 

7. У трикутній призмі вершин є …

    А. 6  Б. 5   В. 4   Г. 7

 

8. У чотирикутній призмі всі бічні грані рівні і площа кожної з них дорівнює 12 см². Бічна поверхня призми дорівнює …

  А. 12 см²  Б. 24 см²  В. 3 см²  Г. 48 см²

 

9. У п’ятикутній призмі площа основи дорівнює 8 см², а площа бічної поверхні 24 см². Площа її повної поверхні дорівнює …

  А. 32 см²  Б. 24 см²  В. 40 см²  Г. 64 см²

 

 

 

 

 

ТЕСТ

ІІ варіант

1.На якому з рисунків зображено призму?

 

 

 

 

            А.                 Б.                 В.                 Г.

 

2.У чотирикутній призмі бічних граней є …

А. 5   Б. 4   В. 6    Г. 10

 

3.У похилій призмі бічні грані …

А. Прямокутники   Б. Паралелограми   

    В. Трапеції    Г. Інша відповідь

 

4.У трикутній призмі всього граней є …

    А. 7   Б. 5   В. 6    Г. 8

 

 

5.На малюнку зображено куб АВСDA₁B₁C₁D₁. Бічним ребром цього куба є …

 

А. АВ Б.D₁D  

B.C₁ D₁           Г. ВС

 

 

 

 

6. У п’ятикутній призмі бічних ребер є …

А. 5  Б. 7   В. 8   Г. 6

 

7. У чотирикутній призмі вершин є …

А. 4  Б. 12   В. 8   Г. 16

 

8. У трикутній призмі площа основи 8 см², а площі бічних граней 10 см², 7 см² і 13 см². Площа повної поверхні призми дорівнює …   

А. 30 см²  Б. 38 см²  В. 46 см²  Г. інша відповідь

 

9.У чотирикутній призмі всі бічні грані рівні і площа кожної з них дорівнює

6 см². Бічна поверхня призми дорівнює …

  А. 12 см²  Б. 24 см²  В. 3 см²  Г. 48 см²

 

 

 

 

ВІДПОВІДІ

 

І варіант.

1.	2.	3.	4.	5.	6.	7.	8.	9.
В.	Б.	А.	Б.	В.	А.	А.	Г.	В.

 

 

 

 

ІІ варіант.

1.	2.	3.	4.	5.	6.	7.	8.	9.
В.	Б.	Б.	Б.	Б.	А.	В.	Б.	Б.

 

 

 

 

 

 

 

 

Додаток 3

 

 

 

 

Поперечний розтин	Фрагмент покрівлі

 

 

 

АС=3,6м  

ВС=2м