Урок "Розв’язування текстових задач на рух"

УРОК 31.

Тема уроку: Розв’язування текстових задач на рух.

Мета уроку:

навчальна: формувати вміння розвязувати задачі на рух;  розглянути основні види текстових задач на рух та етапи їх розвязування;

розвивальна: формувати вміння логічно мислити;

виховна: виховувати свідоме ставлення до навчання.

Тип уроку: : засвоєння нових знань і вмінь.

Хід уроку

I. Організаційний етап.

Перевірити готовність класу до уроку. Налаштування на роботу.

II. Перевірка домашнього завдання.

Перевірити наявність виконання домашнє завдання.

III.  Формулювання мети і завдань уроку.

Завдання уроку навчитися застосовувати рівняння до розв’язування задач.

IV. Актуалізація опорних знань.

Для уроку нам будуть потрібні вміння відтворити ви­конувати дії, за допомогою яких знаходять величини, які «більші на...», «менші на...», а також відповідають на запитання «скільки разом?», «на скільки більше?», «на скільки менше? ». Такі вміння, у свою чергу, сприятимуть формуванню вміння складати рівняння за умовою задачі.

V. Сприймання і засвоєння навчального матеріалу.

Розглянемо основні види текстових задач на рух.

Ми вже багато разів розв’язували задачі на рух і знаємо формулу шляху

що виражає взаємозв’язок величин: s — пройдена відстань (шлях); v — швидкість руху, тобто відстань, яку долають за одиницю часу; t — час руху.

Також знаємо формули, за якими можна знайти швидкість, якщо відомі пройдена відстань та час руху:

та час, якщо відомі пройдена відстань та швидкість:

Зауваження: 1. У задачах на рух будемо вважати, що швидкість руху на всьому шляху не змінювалася.

2. Одиниці вимірювання швидкості (км/год, м/хв, м/с тощо) залежать від умови задачі. Якщо, наприклад, жук за 5 хв проповзає 10 м, то його швидкість 10 : 5 = 2 (м/хв).

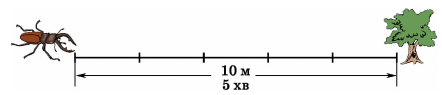
Розглянемо тепер, як розв’язуються задачі на рух по річці. У цих задачах є своя особливість: потрібно розрізняти швидкість руху за течією та швидкість руху проти течії.

Нехай, наприклад, власна швидкість човна (тобто його швидкість у стоячій воді) дорівнює 15 км/год, а швидкість течії річки дорівнює 2 км/год. Тоді швидкість, з якою човен пливе за течією, складається з його власної швидкості та швидкості течії: 15 + 2 = 17 (км/год). А швидкість, з якою човен пливе проти течії, отримуємо відніманням швидкості течії від власної швидкості човна: 15 - 2 = 13 (км/год).

Розглянемо задачі, у яких діють два учасники руху.

Рух з одного пункту з відставанням. Нехай два об’єкти одночасно починають рух в одному напрямі з однієї точки з різними швидкостями

= 5км/год і = 3 км/год.

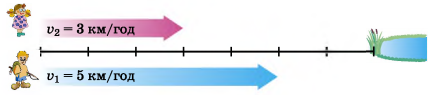
Тоді за першу годину об’єкт випередить об’єкт на 2 км.

Відстань, на яку віддаляються об’єкти за одиницю часу, називають швидкістю віддалення .

У випадку руху двох об’єктів з одного пункту з відставанням (якщо > ).

Через t год між об’єктами буде відстань

Задача 1. Два автомобілі одночасно виїхали в одному напрямі. Швидкість першого автомобіля 60 км/год, швидкість другого 72 км/год. Яка відстань буде між автомобілями через 9 год?

Розв’язання. = (72 – 60) 9 = 12 9 = 108 (км).

Рух з одного пункту в протилежних напрямах. Не хай два об’єкти одночасно починають рух з однієї точки у протилежних напрямах зі швидкостями і  =3 км/год.

Тоді за першу годину об’єкт віддаляється від об’єкта на 8 км. У цьому випадку швидкість віддалення

Через t год між об’єктами буде відстань

Задача 2. Дві черепахи одночасно почали рухатись у протилежних напрямах зі швидкостями 6 дм/хв і 4 дм/хв. Яка буде відстань між черепахами через 35 хв?

Розв’язання. = (6 + 4) 35 = 10 35 = 350 дм.

Рух двох об’єктів назустріч одне одному. Нехай два об’єкти одночасно починають рух назустріч одне одному зі швидкостями   і  =3 км/год, причому початкова відстань між об’єктами більша за 8 км.

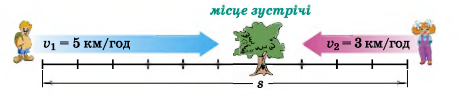
Тоді за першу годину відстань між об’єктами скоротиться на 8 км.

Відстань, на яку зближаються об’єкти за одиницю часу, називають швидкістю зближення .

У випадку руху двох об’єктів назустріч одне одному .

Якщо початкова відстань між об’єктами дорівнює s кіло
метрів і об’єкти зустрілися через год, то очевидно, що

Якщо то через t год відстань між об’єктами
зуст
скоротиться на відстань

Задача 3. Два автобуси виїхали одночасно з двох міст і зустрілися через 5 год. Швидкість одного 45 км/год, а другого на 10 км/год більша. Знайди відстань між містами.

Розв’язання. 1) 45 + 10 = 55 (км/год) — швидкість другого автобуса;

2) (45 + 55) 5 = 500 (км) — відстань між містами.

Рух в одному напрямі навздогін. Нехай два об’єкти одночасно починають рух з різних точок в одному напрямі зі швидкостями і  =3 км/год, причому об’єкт, що має більшу швидкість, рухається позаду і початкова відстань між об’єктами більша за 2 км.

Тоді за першу годину об’єкт стане ближче до об’єкта на 2 км. У цьому випадку

Якщо початкова відстань між об’єктами дорівнює s км і об’єкт наздогнав об’єкт через год, то очевидно, що

Якщо , то через t год відстань між об’єктами скоротиться на відстань

Задача 4. З двох пунктів, відстань між якими 120 км, одночасно почали рух в одному напрямі пішохід зі швидкістю 5 км/год і автобус, який наздоганяв пішохода. Знайди швидкість автобуса, якщо він наздогнав пішохода через 2 год.

Розв’язання. = s : t; = 120 : 2 = 60 (км/год).

Тоді швидкість автобуса дорівнює 60 + 5 = 65 (км/год).

VI. Формування вмінь.

Виконання вправ.

Вправа  415. (Усно). 1) Юний мандрівник з’ясував, що на шлях за течією річки було витрачено менше часу, ніж на той самий шлях проти течії. Чим це можна пояснити, якщо мотор човна працював однаково справно під час усієї подорожі?

2) На шлях по річці від пункту А до пункту В теплохід витратив 3 год, а на зворотний шлях — 2 год 30 хв. У якому напрямі тече річка?

Вправа 416. Знайди невідому величину.

Вправа 420. Швидкість катера у стоячій воді становить 14 км/год, а швидкість течії річки — 2 км/год. Визнач:

1) швидкість катера за течією річки;

2) швидкість катера проти течії річки;

3) шлях, який долає катер за 2 год за течією річки;

4) шлях, який долає катер за 3 год проти течії річки.

Вправа 422. 1) Велосипедисти рухаються у протилежних напрямах. На скільки кілометрів вони віддаляться один від одного за 1 год? 2 год? 5 год?

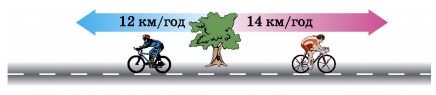
2) Один з пішоходів наздоганяє іншого. На скількілометрів скоротить відстань цей пішохід через 1 год? 2 год? 5 год?

Вправа 426. Катер, власна швидкість якого 18 км/год, плив 2год за течією річки і 3 год проти течії. Яку відстань за цей час подолав катер, якщо швидкість течії річки 2 км/год?

Вправа 434. Відстань між пристанями 72 км. Власна швидкість човна становить 21 км/год. За який час подолає відстань між пристанями цей човен, рухаючись проти течії, якщо, рухаючись за течією, він подолав відстань за 3 год?

VII. Підсумки уроку.

Питання до класу:

1. Як знайти невідому відстань, якщо відомі швидкість і час?

2. Як знайти невідому швидкість, якщо відомі відстань і час?

3. Як знайти невідомий час, якщо відомі відстань і швидкість?

4. Як знайти швидкість руху човна за течією та проти течії, якщо відомі власна швидкість човна та швидкість течії?

5. Як знайти швидкість віддалення, якщо відомі швидкості та   об’єктів, що віддаляються (розглянути два випадки)?

6. Якою буде відстань між цими об’єктами через t год?

7. Як знайти швидкість зближення, якщо відомі швидкості та    об’єктів, що зближуються (розглянути два випадки)?

8. На яку відстань s скоротиться відстань між об’єктами через t год?

9. Як знайти час через який об’єкти зустрінуться, якщо початкова відстань між ними дорівнює s?

VIII. Домашнє завдання.

Опрацювати § 12 ст. 66 – 75

Вправа 423. 1) Машини рухаються в одному напрямі. Яка буде відстань між ними через 1 год? 2 год? 7 год?

2) Велосипедисти рухаються назустріч один одном. На скільки кілометрів наблизяться вони один до одного за 1 год? 2 год? 4 год?