Якушенко І.В., учитель математики Голопристанської спеціалізованої школи І-ІІІ ступенів з поглибленим вивченням предметів філологічного та природничо-математичного циклів

спеціаліст вищої категорії

ПЛАН - КОНСПЕКТ УРОКУ З ГЕОМЕТРІЇ НА ТЕМУ «ОБЧИСЛЕННЯ ПЛОЩІ ПОВЕРХОНЬ МНОГОГРАННИКІВ. РОЗВ’ЯЗУВАННЯ ПРИКЛАДНИХ ЗАДАЧ»

для учнів 11 класу

Мета:   повторити теоретичний матеріал по темі «Площі  поверхонь многогранників». Систематизувати та узагальнити знання учнів. Застосовувати математичні знання під час розв’язування  прикладних задач. Формувати просторову уяву, розвивати бажання пізнавати нове, прививати інтерес до математики. Навчити  застосовувати  набуті знання на практиці.  

Тип уроку: Урок систематизації та узагальнення  вивченого матеріалу.

Тип проекту:  навчальний, дослідницький, творчий. 

За тривалістю підготовки: короткотривалий  (один тиждень).

За кількістю учасників: груповий.                    

Обладнання:  Мультимідійний  комплекс, роздатковий матеріал з поданими 

                          завданнями, мультимедійна презентація до уроку.

                                                                                                                                                    «Теорія без практики  мертва

                                                                                                                                                       І безплідна, практика без

                                                                                                                                                       теорії не можлива»

                                                                                                                                                                                  Рене Декарт

                                                       Хід уроку

І.Організаційна частина. Повідомлення теми та мети уроку.

 А). Перевірка домашнього завдання (Консультанти перевіряють належність домашнього завдання).

ІІ. Актуалізація опорних знань.

«Ті,  хто полюбляє практику без теорії, подібний  до мореплавця, який  зайшов  на корабель без руля і компаса і тому  ніколи не знає, куди він пливе»

                                                                                         Леонардо  да Вінчі

Дослухаємося до  цих слів і пригадаємо теорію.

Запитання до учнів:

1. Як називається многогранник, який складається з двох плоских многокутників, що лежать в різних площинах і суміщаються паралельним перенесенням, і відрізків, які з’єднують відповідні точки цих многокутників? (Призма).
2. Як називаються сторони граней многогранника? (Ребрами).
3. У якій призмі бічні ребра перпендикулярні до основи? (Прямої).
4. Як знайти площу бічної поверхні  прямої призми? (S =H × P).
5. Паралелепіпедом називається призма, в основі якої лежить ..? (Паралелограм).
6. Яка фігура є бічною гранню призми? (Паралелограм, а у прямої призми – прямокутник, у куба – квадрат).
7. Як називається точка в якій сходяться три грані куба? (Вершина куба).
8. Що у прямої призми може бути висотою? (Бічне ребро).
9. Як знайти повну поверхню призми?
10. Довжини непаралельних ребер прямокутного паралелепіпеда називаються… (лінійними вимірами).
11. Пірамідою називається многогранник …
12. Якою фігурою є кожна бічна  грань піраміди? (Трикутник).
13. Чи може прямокутник бути бічною гранню піраміди? ( Не може).
14. Скільки ребер у п’ятикутній  піраміді? (10).
15. Чи існує піраміда, у якої 33 ребра? (Ні). 33 грані (так).
16. Скільки висот можна провести в піраміді? (Одну).

ІІ. Мотивація учбової діяльності

Світ, що нас оточує – це світ геометрії.  Сьогодні на уроці  ми повторимо основні властивості многогранників та формули обчислення їх поверхонь та будемо роз’язувати  прикладні задачі з  даної  теми. Ми повинні переконатися, що наше життя тісно пов’язане  з математикою.  Людина проявляє інтерес до многогранників на протязі всього свого життя.

Назвіть будь ласка де використовують на практиці предмети, які мають форму многогранників? (кубик - рубик, вигляд архітектурної споруди, олівець, брусок, цеглина, будинок …)

Як ви думаєте, чи можливо в житті обійтися і без знаходження площ многогранників? Чи знадобляться вам знання  даної теми у вашому житті?

ІІІ. Основна частина. Розв’язування задач

• Розв’язування задач за готовими рисунками.

(робота в групах).

Задача 1. Основа прямої призми – прямокутний трикутник з катетами 3 і 4 см, висота призми 5см.Знайдіть площу повної поверхні

          призми.

Задача 2. У похилій трикутній призмі відстані  між бічними ребрами    дорівнюють 5см, 12 см  і  9 см. Знайти бічне ребро призми, якщо  її бічна поверхня дорівнює  260 см.

Задача 3. Сторона основи правильної призми дорівнює 12см, а діагональ бічної грані 13 см.  Знайдіть висоту призми.

Задача 4. Знайти площу бічної поверхні прямокутного паралелепіпеда з  вимірами 5 см, 2см і 10см.

Задача 5 . Знайдіть площу поверхні правильної чотирикутної піраміди, сторона  основи якої дорівнює 10 см, а апофема 6 см.

Історична довідка «Звідки пішли назви геометричних фігур»

Майже всі назви геометричних фігур мають грецьке походження, як і саме слово геометрія, що в перекладі означає «землеміряння». Проте здебільшого ці терміни потрапили до нас  не безпосередньо з грецької, а через латинську мову. Є й такі, що прийшли до нас з інших мов. Давайте простежимо, який зміст вкладено в кожний термін.

Призма  - від грецького «присма» (розпиляне, мали на увазі розпиляну колоду).

Паралелепіпед – від грецьких «паралелос» і «епіпедос» (рівний ,плоский).

Куб –прямокутний паралелепіпед, усі виміри якого рівні.

Куб вважають ідеальною формою для споруд.

У Роттердамі знайшли незвичне застосування цієї форми, побудувавши архітектурний комплекс «Кубічні будинки».

 Куб - грецьке «кібос» (гральна кісточка).

Піраміда  –  Єгипетські піраміди… Люди з різних країн світу приїжджають до Єгипту, щоб побачити ці величні споруди, серед яких одне з «семи чудес світу» - піраміда Хеопса.

Великий інтерес викликає  і походження слова «піраміда».  Деякі вчені вважають, що слово «піраміда» виникло від назви солодких пирогів із рисової муки пірамідальної форми, які були популярні  в Давній Греції. Інші вважають, що слово «піраміда» складено з грецьких  слів «піро»- огонь, світ і «мідос»-середина. У багатьох джерелах можна знайти  і таке пояснення:

слово «піраміда» - грецьке, означає многогранник.  Є ще латинська форма грецького «пюраміс»,  яким греки  називали єгипетські   піраміди.

Піраміди усипальниці є і в Україні  на  Полтавщині.  Вони були збудовані  більше ста років тому. Одна  з таких пірамід розташована  в Березовій Рудці. Її висота становить 9м.

Як бачимо, всі назви геометричних  фігур  спочатку були назвами конкретних предметів.

До проведення уроку клас було поділено на дві групи, кожна  з них отримала заздалегідь завдання та працювала над ним. Кожна з них повинна дати відповідь на запитання:  Чи можливо в житті  обійтися  без знаходження площ многогранників? Чи знадобляться вам знання  даної теми у  житті?

Перша група  «Дослідники» працювала над проектом: « Як визначити кількість утеплювача для стін і даху будинку певної форми (ширина будинку - 8 м,  довжина – 9м, висота будинку- 2,5 м з урахуванням дверей та вікон) та  розрахувати ціну  утеплення і можливу економію палива, щоб визначити за який період часу окупиться отеплення.

Друга група «Практики»  отримала завдання  підібрати  або придумати  цікаві задачі  з теми «Площі многогранників», які носять прикладний характер та ознайомити нас з ними.

Один мудрець сказав:  «Дві людини, які обмінялися золотими монетами, не стали багатими. Але,  якщо вони обмінялися  думками, то кожний із них став набагато багатим. Адже обидва стали тепер розумнішими». Обміняймося й ми думками,  ідеями, знаннями. Надамо слово першій групі. (Учні захищають свій проект). Виступ  першої групи (10 хв)

Тепер послухаємо групу «Практики».  Виступ другої групи (10 хв).

Задача 1. Дах будинку  має форму правильної  чотирикутної піраміди,  сторона основи дорівнює 10м, а бічне ребро - 13м. Дах потрібно покрити залізом, розмір листа якого 1м x 1,5 м, а ціна 120 грн за лист. Скільки квадратних метрів покрівельного матеріалу потрібно і яка буде вартість покупки, якщо на з’єднання  витрачається 5% від матеріалу.

Задача 2. Усі люблять подарунки, а особливо робити їх  оригінальними і своїми руками. Випала нагода зробити коробочку для упакування подарунка  у вигляді  форми низької призми з ромбом  в основі. Найбільша відстань між протилежними кутами кришки  становить 24см, а найменша – 10 см. Висота коробки 4 см. Скільки  потрібно квадратних сантиметрів     кольорового  паперу, щоб оклеїти коробку(крім дна)

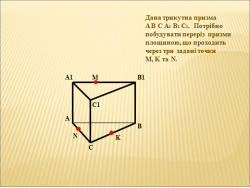
IV. Розв’язування задач

Завдання групам побудувати переріз трикутної призми, що проходить через точки К,М,Р.

Записані на слайді деформовані завдання, означення. Потрібно їх прочитати і знайти помилку.

Завдання «Знайди помилку»

1) Діагоналлю призми називається відрізок, який сполучає дві вершини, які належать одній грані.

2) Бічна поверхня піраміди дорівнює добутку периметра основи на висоту.

3) Кубом називається паралелепіпед, в якого всі ребра рівні.

4) Грані паралелепіпеда паралельні і рівні.

5) Многогранником називається тіло, обмежене  нескінченною кількістю площин.

6) Квадрат діагоналі паралелепіпеда дорівнює сумі квадратів його трьох лінійних вимірів.

7) У трикутній призмі можна провести три діагоналі.

8) Бічними ребрами піраміди називаються відрізки, які сполучають вершину піраміди з будь-якою точкою основи.

9)  Апофемою називається висота бічної грані піраміди.

10) Протилежними називаються грані паралелепіпеда, які мають спільні вершини.

V.  Підсумок уроку

Сьогодні  ми повторили означення, основні властивості геометричних тіл та формули для обчислення площ поверхонь призми, паралелепіпеда та піраміди. Застосовували ці знання  при розв’язуванні задач з прикладним змістом. І як підсумок до уроку хочу нагадати  слова Рене Декарта:

«Теорія без практики мертва І безплідна, практика без теорії не можлива»

Рефлексія

Учні по колу висловлюються одним реченням, обираючи початок фрази з рефлексивного ряду на слайді ( слайд)

- сьогодні я дізнався …;

- було складно…;

- я виконував завдання…;

- я зрозумів, що…;

- тепер я можу…;

- урок дав мені для життя…;

- мені захотілося….

VI. Домашнє завдання

1) Скласти  дві задачі  прикладного змісту на обчислення  площ поверхонь многогранників.

          2) Обчислити повні форми шафи і коробки сірників.