Урок "Застосування формул скороченого множення"

Про матеріал

матеріал для формування вміннь учнів застосовувати вивчений матеріал для розв’язування задач.

Перегляд файлу

Урок алгебри у 7 класі.

Тема. Застосування формул скороченого множення.

Мета:

навчальна: формувати вміння застосовувати вивчений матеріал для розв’язування задач; поглибити знання учнів про застосування формул скороченого множення; провести діагностику засвоєння системи знань і вмінь та її застосування для виконання вправ;

розвивальна: розвивати пізнавальні інтереси, пам'ять, увагу, наочно образне мислення, комунікативні навички; формувати навички контролю і самопізнання;

виховна: виховувати активність,відповідальність, колективізм, доброзичливість.

Тип уроку: узагальнення і систематизація знань.

Девіз уроку:

„ Міцні знання – гарантія успіху»

Епіграф:

Недостатньо тільки отримувати

знання, треба знати їх застосування.

Недостатньо тільки бажати,

треба діяти

Й.-В. Гете

Хід уроку

Організаційний етап

Добрий день, діти! Ми починаємо урок, подумайте і скажіть,

які асоціації викликає у вас слово „урок”?

У – успіх...

Р – радість...

О – обдарованість...

К – компетентність…

Сподіваюсь,що сьогодні на уроці вас чекає успіх і радість. Ви зможете продемонструвати власну обдарованість і компетентність.

Девізом нашого уроку є слова: (читають учні ) „ Міцні знання – гарантія успіху ”

А епіграфом до уроку є слова відомого німецького вченого Гете:

Звичайно «Недостатньо тільки отримувати знання,

треба знати їх застосування.

Недостатньо тільки бажати,

треба діяти»

Отже, давайте діяти. Наскільки ви компетентні у застосуванні всіх способів розкладання многочленів на множники, в тому числі й використанні формул скороченого множення при тотожних перетвореннях многочленів, покаже сьогоднішній урок. У кожного із вас лежить на парті конверт. Відкрийте його і виберіть смайлик, який відповідає вашому настрою. А на звороті ви побачите оцінку. Зафіксуйте цю оцінку на полях зошита і ту, яку б ви бажали отримати.

ІІ. Актуалізація опорних знань.

Наш урок незвичайний. Ми відправляємося в міжгалактичну подорож. Як і для будь-якої подорожі нам треба зібрати валізу. Але валізу не з чашкою, ложкою та іншими речами побуту, а з математичними правилами та законами, якими ви будете користуватися на уроці. Тому дістаньте із схованок пам’яті все те, що вивчали на попередніх уроках.

Завдання номер 1. «Установити відповідність»

О библиотечно-информационном центре (назвати і прочитати формули)

(а +в)²=	(а - в)(а² + ав + в²)
(а - в)²=	(а - в)(а + в)
а²- в² =	(а + в)(а²- ав + в²)
а³+ в³ =	ас - вс
а³ - в³ =	а² + 2ав + в²
(а-в)(а+в)=	а² - 2ав + в²
(а-в)с=	а²- в²

ІІІ. Розв’язування вправ.

№1. Молодці, зібрали формули у валізу, але щоб потрапити на корабель треба придбати квиток. Для цього вам необхідно пройти деякі випробування. А квитки є різні. Вартість квитка залежить від якості салону: чим краще, тим дорожче квиток. Таким чином:

«Клас А» - 9-11;

«Клас В» - 6-8;

«Клас С» -2-5.

Ви, звичайно, зрозуміли, що це оцінки. Купуємо квитки, а математичний диктант допоможе з’ясувати - хто в якому класі полетить.

Математичний диктант

Квадрат числа а;
Подвоєне число в;
Сума виразів х і у;
Сума квадрата х і куба у;
Подвоєний добуток а і в;
Потроєний добуток с і d;
Квадрат суми а і в;
Квадрат різниці х і у;
Добуток в і квадрата а;
Добуток куба в і квадрата а;
Потроєний добуток квадрата а і в.

Перевіримо отримані відповіді і оцінимо свої знання. Дістаньте з конверта свій квиток і у розділі «Білет» поставте ту цифру, яку ви отримали під час написання диктанту.

$C:\Documents and Settings\MS\Рабочий стол\аа\картинка сонячна система.jpg$ БІЛЕТ

$C:\Documents and Settings\MS\Рабочий стол\аа\земля.jpg$

$C:\Documents and Settings\MS\Рабочий стол\аа\венера.jpg$ ЗНАХІДОК

$C:\Documents and Settings\MS\Рабочий стол\аа\нептун.jpg$ ПОМИЛОК

$C:\Documents and Settings\MS\Рабочий стол\планета\images (24).jpg$ ВИПРОБО-ВУВАНЬ

$C:\Documents and Settings\MS\Рабочий стол\планета\images (17).jpg$ ІСТИНИ

$C:\Documents and Settings\MS\Рабочий стол\планета\images (37).jpg$ ВСЬОГО

ПІП

БАЛ

Прошу познайомитися зі змістом квитка. В ньому ви бачите таблицю, де вказані планети – зупинки. Виконуючи завдання, ми мандруватимемо галактикою, отримуючи при цьому бали. На останній зупинці порахуєте кількість отриманих балів, які і будуть вашою оцінкою за урок.

Критерії оцінювання:

Розв’язав все правильно, без помилок – 11б
Під час розв’язання допустив від 1 до 2 помилок – 9б
Під час розв’язання допустив від 3 до 4 помилок – 5б
Під час розв’язання допустив більше 4 помилок – 2б

№ 2. Отже, ви отримали білет на корабель. Ми летимо по галактиці. Перед нами планета «Теоретиків». На цій планеті дуже люблять гру «Доміно». Давайте і ми приймемо участь у цій грі, тільки наше «Доміно» буде математичним.

(картки «доміно» у деяких учнів. Починає той ,у якого записано старт і фініш- він же і закінчує. Цей учень задає стартове запитання. Інші учні повинні слідкувати за перебігом гри,щоб не пропустити свою відповідь. 2бали – правильна відповідь; 0-якщо пропустили; -1-якщо відповідь не правильна)

Планета «Теоретичних знань».

«Математичне доміно».

Фініш: Відповідь: Добутку суми цих виразів на неповний квадрат їх різниці.

Старт: Запитання: Що називають многочленом?

Відповідь: Суму одночленів.

Запитання: Що називають одночленом?

Відповідь: Добуток чисел, змінних та їх степенів.

Запитання: Як помножити одночлен на многочлен?

Відповідь: Одночлен помножити на кожен член многочлена, а результати додати.

Запитання: Як перемножити одночлени?

Відповідь: Перемножити числові коефіцієнти, а потім перемножити степені з однаковими основами і результати перемножити.

Запитання: Як помножити два степеня з однаковими основами?

Відповідь: Основу залишити ту саму, а показники степеня додати.

Запитання: Як піднести степінь до степеня?

Відповідь: Основу залишити ту саму, а показники степенів перемножити.

Запитання: Як помножити многочлен на многочлен?

Відповідь: Кожен член одного многочлена помножити на кожен член другого многочлена і результати додати.

Запитання: Чому дорівнює квадрат суми двох виразів?

Відповідь: Квадрату першого вираза плюс подвоєнний добуток першого на другий плюс квадрат другого виразу.

Запитання: Чому дорівню квадрат різниці?

Відповідь: Квадрату першого виразу мінус подвоєнний добуток першого на другий плюс квадрат другого виразу.

Запитання: Чому дорівнює добуток різниці і суми двох виразів?

Відповідь: Різниці квадратів цих виразів.

Запитання: Чому дорівнює добуток різниці двох виразів на неповний квадрат їх суми?

Відповідь: Різниці кубів цих виразів.

Запитання: Чому дорівнює сума кубів двох виразів?

№ 3. Міжпланетний корабель підлетів до невідомої планети, і сфотографував її поверхню. А ми з вами взяли пробу грунту цієї планети. Разом з пробами знайшли шматок твердого сплаву із загадковими записами. Тому, вам необхідно пояснити, що означають ці загадкові знаки.

Планета «Знахідок» (відновити тотожність).

(а+…)²=…+2…с+с²;

(х+…)(х – …)=х² – 144;

х² –…=(… – у²)(х+…);

m³ –…=(… –n²k³)( m²… … …);

(6х –…)²=36х² –…+1;

(… - …)²= 25p⁴-80p²q +…;

(n –2в)²=n² - …+4в².

Взаємоперевірка! Поміняйтеся роботами і звірте одержані результати із відповідями на екрані.

За критеріями визначте кількість балів і занесіть до таблиці.

№4. Наша подорож триває. Ми дістались планета «Помилок». Давайте заглянемо, що тут відбувається. Жителі цієї планети – ледарі. Вони не можуть розв’язати жодної тотожності і просять нас навчити їх. Давайте їм допоможемо.

Планета «Помилок».

(записати в зошиті правильні тотожності).

49 – с²=(49 – с)(49+с);

(р – 10)²=р² – 20р+10;

х³ – 8у⁶z⁹=(х – 2 уz⁶)(х²+2 у²z³+4 у⁴z¹²);

36а² + 49в²=(6а – 7в)(6а+7в);

а³ + 27в³=(а – 3в)(а +6ав – 9в²);

(5х – 2у)²=25х² – 4у².

Взаємоперевірка! Поміняйтеся роботами і звірте одержані результати із відповідями на екрані.

За критеріями визначте кількість балів і занесіть до таблиці.

Фізкультхвилинка.

Щоб ми могли і надалі творчо працювати і логічно мислити, проведемо фізкультвікторину:

- Якщо ви вважаєте, що вам у житті потрібно вивчати формули,

Підніміть руки

- Якщо ви вважаєте, що вам у житті потрібно вміти швидко зручні рахувати,

То підстрибніть

- Якщо ви вважаєте, що вам у житті необхідно вміти розв’язувати задачі,

То кліпніть очима

- Якщо ви вважаєте, що урок алгебри розвиває логіку вашого мислення,

Покрутіть головою вліво, вправо

- Якщо ви вважаєте, що хороша дисципліна на уроці - це запорука ваших знань,

Зробіть вдих і видих

- Якщо, на вашу думку, ви уважні і дисципліновані на уроці

Сплесніть руками

З вікториною всі гарно впоралися, тож тепер давайте подорожувати далі

№5. А доки ми відпочивали , наш корабель захопили міжгалактичні пірати і відшвартували на планету «Випробовувань». Викупом є вправи на розкладання многочленів на множники, з використанням різних способів:

Планета «Випробовувань»

5а² – 5у²;

2х² + 4ху + 2у²;

81 – (х² + 6х)²;

9 – х² + 2ху – у².

Взаємоперевірка! Поміняйтеся роботами і звірте одержані результати із відповідями на екрані.

За критеріями визначте кількість балів і занесіть до таблиці.

№6. Продовжуємо свою подорож. Перед нами планета «Відшукання істини». Кожного року на ній проводиться Великий Фестиваль Рівнянь. Завітаємо сюди і приймемо участь у цьому фестивалі.

Планета «Відшукання істини».

Видатний фізик Альберт Ейнштейн говорив так: «Мені доводиться ділити час між політикою і рівняннями. Але рівняння, на мою думку, набагато важливіші . Політика існує тільки для конкретного часу, а рівняння будуть існувати вічність».

Отже і ми займемося рівняннями. Спробуємо застосувати формули до розв’язування рівнянь. На дошці записано 5 рівнянь. Кожен із вас буде розв’язувати 2 рівняння. Потім треба буде підійти до дошки, відшукати отриманий результат та прикріпити його зворотною стороною (буквою) до свого рівняння. Якщо вашого результату немає, значить, рівняння розв’язано неправильно.

Розв’яжи рівняння

(x+6)²-(x-5)(x+5)=79 1,5 - У

9x·(x+6)-(3x+1)²=1 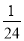- С

a·(8-9a)+40=(6-3a)(6+3a) -0,5 - П

(х-7)²+3=(х-2)(х+2) 4 - І

(2х-3)(2х+3)-8х=7+4х² -2 - Х

Два учні групи розв’язують математичне лото:

(x-5)(x+5)	(a-3)²	4-x²
(6c+7)²	b²-c²	(x-2)(x²+2x+4)

Відповідь:

х² – 25	а² – 6а+9	(2 – х)(2 + х)
Немає сили	могутнішої	за знання;
36с² + 84с+49	(b – c)(b + c)	х³ – 8
людина,	озброєна знаннями,	- непереможна

Взаємоперевірка! Поміняйтеся роботами і звірте одержані результати із відповідями на екрані.

За критеріями визначте кількість балів і занесіть до таблиці.

Це була остання планета нашої Галактиці.

Вершина «Успіху»

І ми повертаємося із нашої подорожі. Але,щоб вона закінчилася успішно, вам необхідно подолати сходинки разом з крокуючим чоловічком і піднятися на вершину «Успіху» нашого уроку. Мета завдання у наступному: знайти легкий шлях обчислення, застосовуючи формули скороченого множення:

31² 49·51

Діти, переконайтеся, що ви правильно виконали завдання і піднялися на вершину успіху.

31²= (30 +1)² = 900 +60 +1 = 961.

49·51= (50 – 1)(50+1) =50² – 1²= 2500 – 1=2499

(Формули скороченого множення використовуються у математичних фокусах, які допомагають виконувати обчислення усно.

Піднесемо до квадрата 85. 85²=(80+5)²=80²+2·80·5+5²=6400+800+25=7200+25=7225. Бачимо,що для обчислення 85² достатньо помножити 8 на 9 і до отриманого результату дописати праворуч 25. Наприклад: 35²=1225 (3·4=12 і до знайденого результату дописали праворуч 25). Щоб ціле число з половиною піднести до квадрату треба помножити на більше сусіднє число і до результату дописати ¼. Наприклад, (6)²=42.) ДОДАТКОВО.

ІV. Підсумок. Ми вже на вершині «Успіху». Тож давайте зробимо привал і запишемо домашнє завдання.

Домашнє завдання: ст. Завдання

Пристебніть пасок, наш корабель заходить у гавань «Підсумків».

Гавань «Підсумків».

Отже, ми у гавані «Підсумків». Підрахувати кількість набраних балів і, у відповідності з таблицею, виставіть оцінки за урок.

12 балів
11 балів
10 балів
9 балів
8 балів
7 балів
6 балів
5 балів
4 бали
3 бали
2 бали
1 бал

Якщо ви порахували оцінки, порівняйте ваш результат з оцінкою, яку ви записали на полях зошита. Виберіть смайлик, що їй відповідає.

VІ. Рефлексія

Комплімент уроку.

- Чи сподобався вам урок?

- Чи справдились ваші очікування?

- Що нового ви навчились на уроці

- Які висновки зробили для себе?

- Чого ви, можливо не уміли робити, а тепер умієте?

- У чому відчували труднощі?

Подорожуючи Галактикою і ви відкрили для себе щось нове, переконалися, що знання формул є досить важливим, оскільки набагато скорочує нашу роботу, а також допомагає при розв’язуванні нестандартних завдань. І цим самим наші сили після цього уроку зміцніли. Тож, я бажаю вам набиратися сил з великою швидкістю, щоб у майбутньому стати непереможними!

Дякую за урок!

Закінчи одне із речень:

“Мені зрозуміло…

“Я запам’ятав…

“Мені на уроці…

“Я думаю…

Немає сили могутнішої за знання; людина, озброєна знаннями, - непереможна

Робота в парах (час обмежений).

Кожній парі роздаються завдання і обмежується час. Перевірка по карточкам з відповідями. №

1. Виконайте дії: а) (5x + 7y)²; б) (14p + 6)²; в)(0,4x – 2a)².

2. Розкладіть на множники: а) x² – 12x + 36; б) 9b² + 6b + 1; в) y² – 20y + 100.

3.Знайти значення виразу: (7p + 4)² -7p(7p – 2), якщо р = 5.

Робота в групі (консультація по розв’язанню, обговорення завдань та їх розв’язків )

Кожному члену групи роздаються завдання рівня А, В, С. Кожен член групи вибирає собі посильне завдання. Перевіряємо по карточкам з відповідями

Рівень А

Розкладіть на множники: а) c² – a² ; б) b² – 4.
Виконайте дії: а) (х - 3)(х + 3); б) (х - 3)².

Рівень В

Спростіть: а) (с + х)² - (с - х)²; б) (р + 7)²+ (р - 6)².
Обчислити: 96² – 86².

Рівень С

Розв’язати рівняння: (2х + 3)² – 7х = (2х – 1)(2х + 1).
Розв’язати рівняння: (12x - 4)(12x + 4)- (12x – 1)² – (4x – 5) = 16.

Карточки (робота в парах)

1. Виконайте дії: а) (5x + 7y)²=25х²+70хy+y²;

б) (14p + 6)²=196p²+168p+36; в)(0,4x – 2a)²=0,16х²-1,6ха+4а²

2. Розкладіть на множники: а) x² – 12x + 36=(х-6)²;

б) 9b² + 6b + 1=(3b+1)²; в) y² – 20y + 100=(y-10)².

3. Знайти значення виразу: (7p + 4)² -7p(7p – 2), якщо р = 5.

(7p + 4) 2 -7p(7p – 2)= 49p2+56p+16-49p2+14p=70p+16=70.5+16=366

Карточки (робота в групі)

Рівень А

Розкладіть на множники: а) c² – a²=(a-c)(a+c) ; б) b² – 4=(b-2)(b+2).
Виконайте дії: а) (х - 3)(х + 3)=x²-9; б) (х - 3)²=x²-6x+9;

Рівень В

Спростіть: а) (с + х)² - (с - х)²=(c+x – c + x)(с+х+с – х)= 2x*2c= =4сx;

б) (р + 7)²+ (р - 6)²= р²+14p+49 + p²-12p+36= p²+2p+85

Обчислити: 96² – 86²=(96-86)(96+86)=10^.182=1820;

Рівень С

Розв’язати рівняння: (2х + 3)² – 7х = (2х – 1)(2х + 1).

4х²+12х+9 – 7х=4х² – 1

4х²+12х – 7х – 4х²= – 1 – 9

5х= – 10

х= – 10:5

х=- 2.

Розв’язати рівняння: (12x - 4)(12x + 4)- (12x – )² – (4x – 5) = 16.

144х²-16-144х²+24х-1-4х+5=16

28х-12=16

28х=16+12

28х=28

х=1

Повертають картки із завданнями на зворотній бік, де знаходять ключ до розв’язання самостійних завдань.
Зачитують отриманий вислів – спочатку варіант 1, потім варіант 2.
Ставлять собі оцінку за урок і відтворюють свій емоційний настрій на картках самооцінювання.

Два учні на місцях – математичне лото

(x-5)(x+5)	(a-3)²	4-x²
(6c+7)²	b²-c²	(x-2)(x²+2x+4)

(4a + *)²= * +* +9b²

(* + *)²= 36m²+* +49b²

(* - 2y)²= * -28xy + *

(* - *)²= 25p⁴-80p²q +*

Планета теоретичних знань

Планета формул

Планета

испытаний

Планета

секретов

Планета нахождения истины

Активность

во время путешествия

Всего баллов

Оценка

docx

Завантажити

Зберегти на потім

Додав(-ла)

Лисакова Ірина Миколаївна

Пов’язані теми

Алгебра, 7 клас, Розробки уроків

Додано

3 лютого 2021

Переглядів

1007

Оцінка розробки

Відгуки відсутні