Вчимося розв’язувати задачі

Авторами була розглянута велика кількість задач із застосуванням команд розгалуження. Деякі з них можна згрупувати за методом розв’язання, а тому вашій увазі пропонується розбиття на категорії, в якому спочатку представлена базова задача з розбором, а потім умови подібних задач.

І категорія. До цієї категорії можна віднести задачі, які у самому формулюванні умови мають алгоритм їх розв’язання. Фактично при розв’язанні цих задач учень записує мовою програмування у формалізованому вигляді словесний опис команди розгалуження. Розглянемо одну з задач.

Умова задачі. Задано значення дійсних чисел a, b, с. Подвоїти ці значення, якщо , і замінити їх абсолютним значенням, якщо це не так.

Розв’язок задачі:

1. Кожна задача починається з уведення вхідних даних. У нашому випадку потрібно ввести три числа.

2. Використовуючи команду розгалуження перевіряємо умову, що вказана в задачі, та виконуємо задані дії: подвоюємо значення змінних при справдженні умови , та замінюємо їх модулем у протилежному випадку. Звернуть увагу на те, що оскільки на кожній гілці умовного оператора вимагається виконання трьох команд присвоєння, оператори будуть складеними та вміщуватися в операторні дужки begin – end.

Фрагмент тексту програми має вигляд:

var a,b,c:real;

begin

   write(‘Input number  ’);  {Уведення вхідних даних}

   readln(a,b,c);

   if (a>=b)and(b>=c)        {Команда розгалуження, що відповідає умові}

   then begin

      a:=2*a; b:=2*b; c:=2*c;

   end

   else begin

      a:=abs(a); b:=abs(b); c:=abs(c);

   end;

   writeln(‘a=’,a:8:2);     {Виведення результатів}

   writeln(‘b=’,b:8:2);     {у відформатованому вигляді}

   writeln(‘c=’,c:8:2);

   readln;

end.

Задачі для самостійного розв’язання:

1. Перевірити, чи є дане дійсне число додатним (більшим нуля).

2. Визначити, чи є дане ціле число від'ємним (менше 0), додатним (більше 0) або нулем (дорівнює 0).

3. Дано два дійсних числа. Яке з них належить відрізку [-5;10]? (більше рівне -5 ТА менше рівне 10).

4. Дано два дійсних числа а та b. Якщо хоча б одне з них нале­жить відрізку [0;15] (більше рівне 0 та менше рівне 15), знайти суму квадратів цих чисел, інак­ше — знайти середнє арифме­тичне.

5. Дано два дійсних числа а та b. Якщо тільки одне з них є додатнім, знайти суму цих чисел, якщо обидва додатні — знайти середнє арифме­тичне, в протилежному випадку – знайти квадрат суми цих чисел.

6. Перетворити значення двох дійсних змінних x та y за таким правилом: якщо значення x та y від’ємні, кожне з них замінити його модулем, якщо від’ємне тільки одне з них, обидва значення збільшити на 0,5, якщо ж обидва значення невід’ємні і жодне з них не належить відрізку [0.5, 2.0], обидва значення зменшити в 10 разів, в усіх інших випадках значення x та y залишити без змін.

7. Дано цілі числа k, m та дійсні числа x, y, z. При замінити модулем значення x, y або z відповідно, а два других значення зменшити на 0.5.

8. В залежності від розміру суми, розмір податку з неї розраховується за такою схемою:

• якщо сума не перевищує деяку величину a, то податок не вираховується;
• якщо сума більше за a, але не перевищує b, то податок складає 20%;
• якщо сума більше за b, але не перевищує c, то податок складає 40%;
• якщо сума більша за c, то податок складає 50%.

Визначити, який податок буде вирахуваний із суми розміром S. Значення a, b та c задаються з клавіатури.

9. За рейтинговою системою оцінка визначається таким чином: якщо сумарний бал учня становить не менше 92% від максимального, то виставляється оцінка 12, якщо не нижче 70%, то виставляється 8, якщо не нижче 50%, то оцінка 5, в інших випадках – оцінка 2. Визначте оцінку учня, якщо він набрав N балів, а максимальне значення сумарного балу становить S.

 

ІІ категорія. Обчислити значення функції. Ці задачі підрозділяються на дві підгрупи:

• вираз, що підлягає обчисленню, містить операції, які не завжди можна виконати: ділення (ділення на нуль заборонено) або обчислення квадратного кореня (підкореневий вираз не може бути від’ємним);
• для різних значень аргументу обчислення виконуються за різними співвідношеннями.

Розглянемо приклади розв’язання таких задач.

Задача ІІ.1. Обчислити значення функції

Розв’язок задачі:

Очевидно, що обчислення можливі при виконанні двох умов: знаменник не дорівнює 0 та підкореневий вираз невід’ємний. Якщо хоч одна з умов є хибною, виведемо на екран повідомлення про помилку.

Фрагмент тексту програми має вигляд:

var x,y:real;

begin

   write(‘Input number  ’);

   readln(x);

   if (2*x-10>=0)and(sqr(x)-1<>0)

   then begin

      y:=sqrt(2*x-10)/(sqr(x)-1);

      writeln(‘y=’,y:0:2);

   end

   else writeln(‘Error’);

   readln;

end.

Задача ІІ.2. Дано дійсне число x. Обчислити значення функції

Розв’язок задачі:

Вибір співвідношення, за яким виконується обчислення функції, залежить від значення аргументу. Якщо x>10, то обчислюємо за першою формулою, в протилежному випадку – за другою.

Фрагмент тексту програми має вигляд:

var x,y:real;

begin

   write(‘Input number  ’);

   readln(x);

   if x>10

   then y:=sin(x*x*x)

   else y:=sqrt(10-x);

   writeln(‘y=’,y:0:3);

   readln;

end.

Задачі для самостійного розв’язання:

1.       Дано дійсні значення x та y. Обчислити значення величини

.

1.       При заданому дійсному значенні x обчислити

.

2.       Обчислити значення функції для дійсного значення аргументу

.

3.       Дано значення дійсної величини x. Обчислити:
4.       Дано дійсне число x Обчислити f(x) якщо:

5.       Обчислити значення функції

6.       Обчислити значення функції для дійсних значень аргументу:

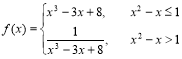
7.       Дано дійсне число x. Обчислити значення функції

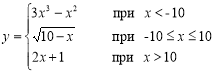
8.       Дано дійсне значення x. Обчислити

 

9.       Найдіть полярні координати r та  на площині за її прямокутними координатами x та y. При цьому скористайтеся формулами:

Примітка: Задачі №7 та №8 можуть бути розв’язані по різному. Найпростіший метод, це записати обчислення для кожного інтервалу аргументу у вигляді скороченого оператору розгалуження. Кількість операторів, очевидно, в цьому випадку буде дорівнювати кількості інтервалів. Однак, цей метод не дуже оптимальний за часом, оскільки за будь-яких початкових значень аргументу (навіть, коли обчислення відбудуться на першому ж інтервалі) перевірка умови буде виконуватись три (для задачі №7) або чотири (для задачі №8) рази. А тому рекомендується записувати розв’язок з використанням вкладених умовних операторів. Задача № 7 при такому підході вимагає використання двох вкладених операторів розгалуження, оскільки має три інтервали для обчислення, а задача №8, відповідно, потребує трьох операторів розгалуження. Пропонуємо Вам самостійно записати ці розв’язки. Для задачі №9 підхід може бути аналогічним.

 

ІІІ категорія. Знайти максимальне (мінімальне) значення з двох (трьох) чисел.

Умова задачі. Дано два числа. Знайти серед них число з найбільшим значенням.

Розв’язок задачі:

У запропонованій задачі вперше ми стикнулися з ситуацією, коли в умові не оговорені типи вхідних значень. Такі задачі зустрічаються досить часто, оскільки програмування, як прикладна дисципліна, вимагає від програміста вміння аналізувати можливі варіанти вхідних даних та обробляти усі ситуації, навіть такі, що здаються неможливими з точки зору «здорового глузду». Адже користувачем програми іноді може бути людина недосвідчена, а іноді і така, що навмисно буде намагатися привести до аварійного завершення програми.

Запропонована задача, очевидно, повинна вміти обробляти будь-які числа (цілі або дійсні), а тому всі змінні для програми має сенс вибирати дійсними, щоб надати можливість працювати як з цілими (вони є підмножиною дійсних чисел) так і з дробовими числами.

Крім того, зауважимо, що має сенс увести ще одну змінну, яка буде зберігати знайдене максимальне значення, оскільки в більшості випадків сам пошук максимуму буду підзадачею деякої іншої задачі, що використовуватиме знайдене найбільше значення для подальших обрахунків. Зверніть також увагу, що при рівних числах з точки зору програмування вони обидва є максимальними, а тому така ситуація окремо не обробляється і максимуму надається будь-яке з двох значень.

Фрагмент тексту програми має вигляд:

var x,y,max:real;

begin

   write(‘Input numbers  ’);

   readln(x,y);

   if x>y         {Умову можна переформулювати, як x>=y}

   then max:=x

   else max:=y;

   writeln(‘max=’,max:0:2);

   readln;

end.

При пошуку максимуму з трьох чисел можна отримати розв’язок трьома методами. Пропонуємо подумати, який із запропонованих нижче розв’язків буде оптимальнішим за часом (менша кількість зайвих перевірок).

1 метод. Трьох чисел максимальне може бути тільки одне з них, а тому можна отримати три ситуації, які обробляються скороченими оператора розгалуження:

   if (x>=y)and(x>=z) then max:=x;

   if (y>=x)and(y>=z) then max:=y;

   if (z>=x)and(z>=y) then max:=z;

2 метод. При пошуку максимального значення з трьох чисел можна спочатку знайти максимум з двох чисел, а потім максимум зі знайденого максимуму та третього числа. Тобто

   if x>y

   then max:=x

   else max:=y;

   if max<z

   then max:=z;

3 метод. Підхід пошуку максимуму не змінюється відносно попереднього випадку, змінюється тільки форма запису:

   if x>y

   then {На цій гілці більшим з двох (x або y) є x}

        if x>z

        then max:=x

        else max:=z

   else {На цій гілці більшим з двох (x або y) є y}

        if y>z

        then max:=y

        else max:=z;

Задачі для самостійного розв’язання:

1.     Дано два довільних числа. Більше з цих чисел за­мінити даним числом m
2.     Дано значення трьох дійсних змінних x, y, z. Змінити їх значення, надавши їм найбільшого із заданих значень.
3.     Дано три числа а, b, с. Найбільше з цих чисел замінити їх середнім ариф­метичним.
4.     Дано дійсне число х. Надрукувати в порядку зростання числа
5.     Дано значення цілих величин a, b, x та y. Знайти .
6.     Дано значення цілих величин x та y. Знайти
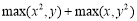
7.     Для заданих значень x, y запишіть програму обчислення виразу:

8.     Обчислити значення виразу

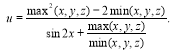
9.     Обчислити значення виразу , де , ,

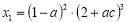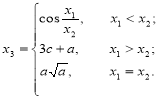
10. З'ясувати, чи можна з да­них трьох чисел А, В, С утвори­ти арифметичну прогресію. Якщо можна, то вивести ці числа на екран у порядку зростання. В протилежному випадку вивести на екран повідомлення, що це не прогресія, наприклад, «NO».
11. Перевірити, чи пройде цеглина з ребрами А, В, С у пря­мокутний отвір зі сторонами Х, У. Вставляти цеглину в отвір доз­воляється тільки так, щоб кожне з її ребер було паралельне чи перпендикулярне до кожної зі сторін отвору.

Примітка: Задача №10 потребує деяких знань з математики, а саме, членами арифметичної прогресії є такі числа, для яких справджується правило: кожне наступне число відрізняється від попереднього на деяку постійну величину, що зветься знаменником арифметичної прогресії. Звідси випливає і розв’язок задачі: спочатку має сенс знайти максимальне з трьох чисел, потім найбільше з тих, що залишилися, а потім, розташувавши їх у порядку зростання, знайти різницю між першими двома та другими двома. Якщо різниці однакові, числа утворюють арифметичну прогресію.

Можливо не відразу зрозуміло, чому задача №11 потрапила у категорію задач пошуку максимуму (мінімуму), але давайте поміркуємо. Очевидно, що цеглина за заданих умов тільки тоді пройде у отвір, якщо її мінімальний вимір буде не більше мінімального виміру отвору, а її середній вимір (не мінімальний і не максимальний) не перевищує максимального розміру отвору. От вам і пошук мінімуму та максимуму!

 

ІV категорія. Задачі про координатну площину. Більшість цих задач пов’язана з визначенням належності точки визначеної області координатної площини.

Умова задачі. Не будемо розглядати очевидні задачі типу, якій чверті координатної площини належить задана точка, а розглянемо задачу з більш складною областю, що відмічена штриховкою. Наприклад таку:

 

 

 

 

 

 

 

 

Розв’язок задачі:

Задачі такого типу розв’язуються, виходячи з наступних міркувань: щоб точка лежала на прямій, потрібно справдження рівності, в якій координати точки підставляються у рівняння заданої прямої. Відповідно, якщо точка не лежить на прямій, рівність перетворюється на нерівність, причому нижче прямої у нерівність типу , а якщо вище, то – , де – функція, що описує рівняння прямої. Рівняння прямої можна отримати кількома методами, але найпростіший – це використання рівняння прямої, що проходить через дві точки з координатами та :

Запропонована задача дозволяє рівняння прямої взагалі отримати без вказаного співвідношення, оскільки прямі є горизонтальними або вертикальними. Для верхньої горизонталі це рівняння буде y=2, для нижньої – y=-2, для лівої вертикалі x=-2, а для правої x=3.

Точка буде лежати всередині заштрихованої області, якщо справджуються усі нерівності для чотирьох прямих. Зверніть увагу, що намальовані прямі бувають штриховими, а бувають суцільними. В першому випадку вважається, що точка, яка лежить на прямій, не належить заштрихованій області, а в другому – належить. Відповідно, в першому випадку нерівність буде строга, а в другому – нестрога.

Оскільки результатом розв’язка задачі буде відповідь «належить» або «не належить» точка вказаній області, будемо виводити на екран повідомлення «Yes» або «No» відповідно.

Фрагмент тексту програми має вигляд:

var x,y:real;

begin

   write(‘Input point  ’);

   readln(x,y);

   if (x>-2)and(x<=3)and(y>-2)and(y<=2)

   then writeln(‘Yes’)

   else writeln(‘No’);

   readln;

end.

У якості ліній, які обмежують задану область можуть бути також графіки функції. Підхід до розв’язання такої задачі не змінюється, тільки у якості функції будуть використовуватися відповідні функціональні залежності. Нагадаємо, що круг має наступну функціональну залежність , де (a,b) – координати центра круга, а R – його радіус.

Задачі для самостійного розв’язання:

1.     Дано координати точки на координатній площині. Визначити, чи лежить ця точка у перший (другій, третій, четвертій) чверті координатної площини.
2.     Визначити, чи лежить точка на осі координат, і якщо лежить, то на якій конкретно.
3.     Визначити, якій чверті координатної площини належить точка з координатами (x,y).
4.     З'ясувати, чи є точки та симетричними відносно:

• осі абсцис;
• осі ординат;
• початку координат.

5.     З'ясувати, чи належить точка (X, Y) кругу радіуса R з цен­тром у точці (а, b).
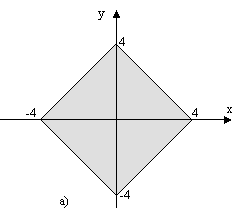
6.     Чи належить точка з координатами (x,y) заштрихованій області

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

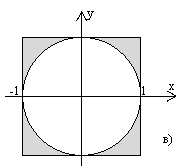
Примітка. Очевидно, що кількість простих умов в завданнях від а) до д) дорівнює кількості ліній, які обмежують область:

1. чотири прямих, функції для яких задаються за допомогою наведеної вище формули;
2. дві прямих (вісь y та горизонтальна пряма, що проходить через точку x=10) та графік функції ;
3. чотири прямих, що утворюю квадрат (всередині квадрату) та функція кола з радіусом 1 та центром у початку координат (зовні кола);
4. дві прямих (y = x та y = –x) та коло з центром у початку координат та радіусом 7 (всередині кола);
5. дві прямих та коло з центром в центрі координат та радіусом 2 (всередині кола).

Усі прості умови поєднуються логічною операцією and, оскільки тільки одночасне справдження всіх умов забезпечить попадання точки всередину заштрихованої області.

Завдання є) виконується аналогічно тільки прості умови поєднуються логічною операцією or, оскільки точка в даному випадку лежить або над однією прямою, або під другою прямою, або ліворуч від, або праворуч від… Для перевірки правильності відповіді спробуйте заштрихувати області згідно умови і на перетині усіх штриховок буде видима відповідь.

Для завдань є) та е) розв’язок складніше, оскільки прямою штриховкою результату досягти не можна. Пов’язано це з тим, що фігури, які отримані лініями, є не опуклими. Для отримання відповіді в цьому випадку необхідно розбити зображення на кілька частин, кожна з яких буде опуклою фігурою. Це дозволить виконати завдання, застосовуючи метод «прямої штриховки» (прості умови, об’єднані логічною операцією and). Запропоновані завдання дозволяють розбивати фігуру на дві частини:

• для завдання є) – ліву та праву відносно осі y;
• для завдання ж) верхню та нижню відносно нижньої горизонтальної прямої.

Для кожної з частин застосовується метод, що наведений вище, а між собою умови поєднуються логічною операцією or, оскільки точка можне належати або перший фігурі, або другій.

 

V категорія. Геометричні задачі. Ці задачі також можна умовно поділити на задачі кількох підгруп:

1. задачі на можливість існування певної фігури – трикутника, квадрата, ромба, прямокутника тощо;
2. задачі на різновиди трикутників – прямокутний, гострокутний, тупокутний або рівносторонній, рівнобічний, різносторонній;
3. належність точки прямій.

Задача V.1. Дано три числа a, b та c. З’ясувати, чи можна побудувати трикутник, довжини сторін якого дорівнюють цим числам.

Розв’язок задачі:

У задачах даної категорії вперше з’являється поняття некоректних вхідних даних. Так, наприклад, довжини сторін не можуть бути від’ємними або нульовими. А тому після уведення вхідних даних обов’язково потрібно перевірити їх коректність і, якщо дані некоректні, вивести про це повідомлення. Спроба використати беззнакові цілі типи для збереження вхідних даних не є слушною, оскільки довжини довільних трикутників можуть мати дробові значення.

Тепер розглянемо математичну модель задачі. Очевидно, що навіть маючи три додатних числа, ми не завжди зможемо побудувати трикутник з такими сторонами. З курсу математики учням відоме таке правило: трикутник можна побудувати тоді і тільки тоді, коли сума довжин двох менших сторін буде більшою за довжину третьої сторони. Часто стереотип мислення помилково підказує, що меншими повинні бути сторони a та b, а с – це найбільша сторона. І тому на прикладі цієї задачі потрібно привчати учнів розглядати всі можливі випадки і перевіряти всі умови. Для даної задачі можливі три випадки, коли найбільшою буде одна з трьох сторін і тому повний розв’язок буде містить складену умову з трьох простих умов, поєднаних логічною операцією and (одночасне справдження трьох умов). Відповідь у цій задачі, як і раніше, буде у вигляді «YES» або «NO» в залежності від того можна чи не можна побудувати трикутник.

Фрагмент тексту програми має вигляд:

var a,b,c:real;

begin

   write(‘Input numbers  ’);

   readln(a,b,c);

   if (a<=0)or(b<=0)or(c<=0)   {Перевірка коректності вхідних даних}

   then writeln(‘Input error’)

   else if (a+b>c)and(a+c>b)and(c+b>a)

        then writeln(‘YES’)

        else writeln(‘NO’);

   readln;

end.

Зауважимо, що теоретично відповідь можна виводити будь-якими літерами (великими чи малими), оскільки людина сприймає їх зміст однаково. Але, готуючись до машинної перевірки розв’язків, можна привчати учнів до строгості навіть у цьому, чітко оговорюючи, якими саме літерами потрібно виводити результат.

Очевидно, що фігуру можна задавати не тільки довжинами сторін. Можна ще задати її координатами вершин. У цьому випадку, використовуючи відомі формули обчислення довжини відрізка заданого координатами його кінців, можна знайти довжини сторін та звести задачу до попередньої. Згідно малюнка довжина відрізка обчислюється за формулою . Некоректних даних у цьому випадку бути не може, але точки можуть лежати на одній прямій, утворюючи вироджену фігуру. Перевірку, чи лежать точки на одній прямій ми розглянемо трохи пізніше.

Трикутник також може бути задано величинами його кутів. Некоректність вхідних даних у цьому випадку перевіряється так само, як і для довжин сторін, а можливість існування трикутника забезпечується відомим математичним співвідношенням, що сума кутів трикутника повинна дорівнювати .

Для чотирикутника перевірка відбувається так само, але математична модель трохи інша:

• для чотирикутника, що заданий довжинами сторін, сума довжин трьох сторін більше четвертої;
• для чотирикутника, що заданий величинами кутів, сума кутів чотирикутника дорівнює .

Задачі для самостійного розв’язання:

1.              Дано два числа. Чи можуть вони бути кутами деякого трикутника? Якщо так, то обчислити величину третього кута.
2.              Дано координати трьох точок на площині. Знайти площу трикутника, утвореного цими точками.
3.              Дано точки А (x₁,y₁), В(x₂,y₂), С(x₃,y₃) та D(x₄,y₄). З'ясува­ти, чи є точка D центром кола, що проходить через точки А, В, С.
4.              Дано координати чотирьох точок на площині. Визначити, чи можна, з’єднавши ці точки в порядку, що задається уведенням, утворити ромб? Якщо так, то обчислити його площу.
5.              З'ясувати, чи існує чоти­рикутник з даними довжинами сторін (а, b, с, d — натуральні числа). Чи може він бути:

1. па­ралелограмом;
2. ромбом.

6.              Дано координати чотирьох точок на площині. Визначити, чи можна, з’єднавши ці точки в заданому порядку, утворити прямокутник? Якщо так, то обчислити його площу.

Тип чотирикутника визначається просто:

•     ромб має всі сторони рівні;
•     у паралелограма сторони попарно рівні;
•     у квадрата та прямокутника ще повинні бути кути прямими (див. задачу V.2).

Задача V.2. Дано три числа a, b та c. Визначити чи є трикутник, довжини сторін якого дорівнюють заданим числам, прямокутним.

Розв’язок задачі:

Задачі даного типу є продовженням попереднього, оскільки її повний розв’язок передбачає спочатку перевірку можливості існування даного трикутника. Зверніть увагу, що теоретично задані числа можуть бути і кутами трикутника. І крім того, можна ще задавати трикутник координатами точок на площині. У перших двох випадках (сторони і кути) потрібно обов’язково перевіряти коректність вхідних даних.

Якщо трикутник існує, то визначення, чи є він прямокутним, виконується з використанням теореми Піфагора. Зауважимо при цьому, що шкільний стереотип, який наголошує, що a та b – катети, а с – гіпотенуза, є необов’язковим у програмуванні. А тому потрібно перевірити три можливих випадки справдження цього рівняння.

Фрагмент тексту програми має вигляд:

var a,b,c:real;

begin

   write(‘Input numbers  ’);

   readln(a,b,c);

   if (a<=0)or(b<=0)or(c<=0)   {Перевірка коректності вхідних даних}

   then writeln(‘Input error’)

   else if (a+b>c)and(a+c>b)and(c+b>a)  {Перевірка можливості побудови}

        then if (a*a+b*b=c*c)or(a*a+c*c=b*b)or(c*c+b*b=a*a)

             then writeln(‘Right triangel’)

             else writeln(‘Not right triangel’)

        else writeln(‘NO’);

   readln;

end.

Якщо a, b, c – кути трикутника, перевірка виявляється ще простішою. В цьому випадку потрібно переконатися, що принаймні один кут (будь-який з трьох) має величину : (a=90)or(b=90)or(c=90).

Якщо ж трикутник заданий координатами своїх вершин, потрібно обчислити довжини сторін за наведеною вище формулою, а потім перевірити трикутник за довжинами сторін. Нагадуємо, що в цьому випадку при обчисленні довжин сторін достатньо сильно накопичується похибка обчислень і теорема Піфагора може не справджуватися навіть для візуально прямокутного трикутника. Тоді варто пригадати правило, на якому ми наголошували ще тоді, коли тільки починали програмувати: порівняння дійсних чисел на точну рівність не зовсім коректно. Потрібно виконувати порівняння з певною, наперед заданою точністю. Так, для розглядуваної задачі, похибка обчислень може досягати 0.0001, що приводить до наступного вигляду умови:

(abs(a*a+b*b-c*c)<=0.0001)or(abs(c*c+b*b-a*a)<=0.0001)

or(abs(a*a+c*c-b*b)<=0.0001)

Для перевірки трикутника на гострокутність та тупокутність перетворюємо рівність на нерівність, не забуваючи, що у тупокутного трикутника тільки один кут може бути тупим, а у гострокутного трикутника усі три кути – гострі (менші ). Теорема Піфагора також перетворюється на нерівність: у тупокутного трикутника сума квадратів сторін більша за квадрат третьої сторони, а у госторокутного – менше.

Перевірка трикутника на рівносторонність та рівнобічність не повинна викликати труднощів.

Задачі для самостійного розв’язання:

1.            З'ясувати, чи існує три­кутник з даною градусною мірою двох внутрішніх кутів. Визначи­ти, чи є він прямокутним, гостро­кутним чи тупокутним.
2.            Дано три числа. Якщо вони можуть бути сторонами різностороннього тупокутного трикутника, виведіть їх в порядку зростання та обчисліть площу цього трикутника.
3.            Трикутник задано величинами своїх кутів. Записати програму, яка визначає, чи являється цей трикутник тупокутним (прямокутним, гострокутним).
4.            Трикутник задано координатами своїх вершин. Записати програму, яка визначає, чи являється цей трикутник рівностороннім (рівнобічним).
5.            Трикутник задано довжинами своїх сторін. Визначити тип трикутника (прямокутний, гострокутний, тупокутний, рівностороній, рівнобічний).
6.            Скласти програму, яка визначає, чи є два заданих трикутника рівними (трикутники задано координатами своїх вершин).

Задача V.3. Дано координати трьох точок на координатній площині. Визначити, чи лежать ці точки на одній прямій.

Розв’язок задачі:

Для розв’язання даного класу задач знову повернемось до рівняння прямої, що проходить через дві точки:

Очевидно, що якщо всі задані точки лежать на одній прямій, підстановка координат третьої точки в рівняння прямої повинно перетворити рівняння у рівність. Рекомендуємо при цьому позбавитись у рівнянні операції ділення нескладним алгебраїчним перетворенням:

.

Фрагмент тексту програми має вигляд:

var x1,y1,x2,y1,x3,y3:real;

begin

   write(‘Input points 1  ’);

   readln(x1,y1);

   write(‘Input points 2  ’);

   readln(x2,y2);

   write(‘Input points 3  ’);

   readln(x3,y3);

   if (x3-x1)*(y1-y2)=(y3-y1)*(x1-x2)

   then writeln(‘Straight line’)

   else writeln(‘Not straight line’);

   readln;

end.

Знаходження точки не на прямій перетворює рівність у нерівність. Це можна застосовувати для перевірки, чи лежать дві точки по один бік від прямої: якщо дві точки лежать по один бік прямої, нерівності повинні мати однаковий знак. Цю умову можна записати двома методами. Перший «лобовий» передбачає, що для обох нерівностей ми розглядаємо спочатку знак менше, а потім більше (або навпаки):

     ((x3-x1)*(y1-y2)<(y3-y1)*(x1-x2))and((x4-x1)*(y1-y2)<(y4-y1)*(x1-x2))

or((x3-x1)*(y1-y2)>(y3-y1)*(x1-x2))and((x4-x1)*(y1-y2)>(y4-y1)*(x1-x2))

А другий – компактніший – ґрунтується на тому, що добуток двох чисел однакового знаку буде завжди додатнім. Замінивши знак порівняння на знак віднімання ми отримаємо для першої половини умови від’ємний результат, а для другої – додатній. Відповідно, якщо обидві нерівності мали однаковий знак, добуток цих двох дужок буде додатним:

((x3-x1)*(y1-y2)-(y3-y1)*(x1-x2))*((x4-x1)*(y1-y2)-(y4-y1)*(x1-x2))>0

Задачі для самостійного розв’язання:

1. Дано точки 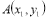, , 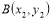. Визначити, чи є век­тори AB i BC перпендикулярними (підказка: теорема Піфагора).
2. Дано точки 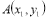, , 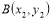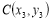. Визначити, чи є век­тори AB i BC колінеарними (підказка: колінеарні вектори лежать або на паралельних прямих, або на одній).
3. Два відрізки прямих задано координатами кінців 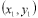, та , . Визначити, чи належать ці відрізки одній прямій (підказка: всі точки повинні бути на одній прямій).
4. Трикутник на площині заданий координатами своїх вершин. Визначити, чи належить центр координат цьому трикутнику (підказка: перевірка трьох умов, кожна з яких перевіряє, чи лежать центр координат та одна з вершин по один бік від двох інших вершин – дивись рис.1).
5. Визначити, чи належить точка (х, у) трикутнику з верши­нами А (x₁,y₁), В(x₂,y₂), С(x₃,y₃).
6. Два відрізки прямих задано координатами кінців (x₁,y₁), (x₂, y₂) та (x₃, y₃), (x₄, y₄). Чи є відрізки частинами деякого третього відрізка і мають спільну частину?
7. Два відрізки прямих задано координатами кінців (x₁,y₁), (x₂, y₂) та (x₃, y₃), (x₄, y₄). Визначити, збігаються ці відрізки хоча б одним зі своїх кінців та лежать на одній прямій, утворюючи при цьому новий відрізок? Вказати координати кінців утвореного відрізка.
8. З'ясувати, чи симетричні точки (x1,y1) та (x2,y2) відносно прямої ах+bу+с=0 (підказка: точки повинні, по-перше, перетворювати рівність на нерівності різного знаку, а по-друге, відстані від кожної точки до прямої повинні бути рівними).
9. Три відрізки прямих задано координатами кінців (x1,y1), (x2,y2); (x3,y3), (x4,y4) та (x5,y5), (x6,y6) і не мають спільних точок. Визначити, чи лежать вони на одній прямій і який з них є «внутрішнім» відносно двох інших (підказка: бажано спочатку «відсортувати» відрізки, тобто розібратися з лівими та правими кінцями відрізків, щоб перша координата була завжди меншою).
10. Два трикутники задано координатами своїх вершин. Визначити взаємне розташування цих трикутників:

• перший всередині другого;
• другий всередині першого;
• трикутники перетинаються;
• трикутники відокремлені один від одного.

Підказка: якщо один трикутник всередині іншого, всі його вершини всередині другого трикутника; а якщо перетинаються, то всередині не більше двох вершин.

11. Дано дійсні числа a, b, c, d, s, t, u (s та t одночасно не рівні 0). Відомо, що точки (a,b) і (c,d) не лежать на одній прямій, що задана рівнянням sx+ty+u=0 та розбиває координатну площину на дві півплощини. З’ясувати, чи вірно, що точки (a,b) і (c,d) належать різним півплощинам (підказка: задача аналогічна перевірці точок, що лежать по різні боки від прямої).

 

VІ категорія. Задачі на перевірку властивостей цілих чисел. Майже всі ці задачі передбачають розбиття числа на окремі цифри з наступним їх аналізом.

Умова задачі. Дано чотирицифрове натуральне число N. Перевірити, чи є це число:

• паліндромом (число, яке читається з обох боків однаково, наприклад, 1331);
• щасливим (сума перших двох цифр числа дорівнює сумі других двох, наприклад, 1203);
• таким, що всі його цифри парні.

Розв’язок задачі:

Ці задачі, по-перше, також вимагають перевірки коректності вхідних даних, оскільки розбиття числа на цифри залежить від їх кількості. По-друге, щоб розбити число на цифри, потрібно застосувати операції цілочисельного ділення та знаходження залишку від цілочисельного ділення числа на 10. Так, наприклад, операція N mod 10 дозволяє отримати останню цифру числа (цифру одиниць), оскільки залишок від ділення числа на 10 дорівнює саме цій цифрі, а операція N div 10 дозволяє «відкинути» цифру від числа. Не пояснюючи докладно усі команди, наведемо ті, які дозволяють отримати з чотирицифрового числа його окремі цифри (цифри нумеруються справа наліво):

c1:=N mod 10;

c2:=(N div 10) mod 10;

c3:=(N div 100) mod 10;

c4:=N div 1000;

Далі розв’язок стає очевидним, оскільки потрібно або порівняти відповідні цифри, або знайти суму деяких цифр, або перевірити властивості самих цифр.

Фрагмент тексту програми має вигляд:

var c1,c2,c3,c4:byte; N:word;

begin

   write(‘Input numbers  ’);

   readln(N);

   if (N<1000)or(N>9999)     {Перевірка коректності вхідних даних}

   then writeln(‘Input error’)

   else begin

         c1:=N mod 10;

         c2:=(N div 10) mod 10;

         c3:=(N div 100) mod 10;

         c4:=N div 1000;

         if (c1=c4)and(c2=c3   {Крайні та середні цифри рівні між собою}

         then writeln(‘Palindrom’)

         else writeln(‘Not palindrom’);

         if c1+c2=c3+c4        {Сума перших двох цифр дорівнює сум двох останніх}

         then writeln(‘Happy)

         else writeln(‘Not happy);

         if (c1 mod 2 = 0)and(c2 mod 2 = 0)and(c3 mod 2 = 0)and(c4 mod 2 = 0)

         {кожна цифра числа є парною}

         then writeln(‘Numbers parity’)

         else writeln(‘Numbers not parity’);

   end;

   readln;

end.

Інша кількість цифр числа змінює тільки формули для отримання цифр числа, причому співвідношення змінюються тільки для старших цифр.

Задачі для самостійного розв’язання:

1. Дано ціле шестицифрове число. Перевірити, чи є воно щасливим, тобто сума перших трьох його цифр дорівнює сумі трьох останніх.
2. Дано ціле трицифрове число. Визначити, чи вірно те, що воно містить рівно дві однакових цифри.
3. Дано ціле шестицифрове число. Чи є воно симетричним (перша половина числа співпадає з другою)? Наприклад, 124124, 221221, 783783 і т.д.
4. Дано ціле п’ятицифрове число N. Перевірити, чи є це число таким, що сума його цифр є числом, що кратне деякому числу P, введеному з клавіатури?
5. Визначити, чи є трицифрове число таким, що сума кубів його цифр дорівнює самому числу (наприклад, ).
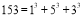6. Дано ціле шестицифрове число. Перевірити, чи є воно таким, що сума його цифр, що стоять на парних місцях, дорівнює сумі цифр, що стоять на непарних місцях.
7. Дано ціле чотирицифрове число. Перевірити, чи чергуються в ньому парні та непарні цифри. Наприклад, такими є числа 1254 або 2781.
8. Автоморфним називається таке число, яке дорівнює останнім цифрам свого квадрата, наприклад, 5²=25, 25²=625. Скласти програму, що визначає, чи являється дане двоцифрове число автоморфним.

 

VІІ категорія. Задачі на розв’язання рівнянь або нерівностей. Для цих задач спочатку дуже важливою є побудова математичної моделі. Так, для лінійного рівняння потрібно розглянути наступні випадки:

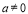• у цьому випадку рівняння має єдиний корінь ;
• у цьому випадку можливі дві ситуації: якщо друге число b дорівнює нулю, рівняння має безліч розв’язків, у протилежному випадку – розв’язків взагалі немає.

Пропонуємо вам за описом математичної моделі розв’язання лінійного рівняння записати програму. А тепер розглянемо іншу часто використовувану задачу.

Умова задачі. Дано три числа a, b, c. Знайти корені квадратного рівняння

Розв’язок задачі:

Ця задача має багато підходів до розв’язання, які залежать від вхідних даних.

По-перше, якщо перший коефіцієнт дорівнює нулю, можливі дві реакції:

• рівняння не квадратне, вхідні дані некоректні;
• рівняння вироджене і тоді в залежності від інших коефіцієнтів можна отримати відповідь «безліч розв’язків» (всі коефіцієнти нульові), «немає розв’язків» (коефіцієнти при змінній нульові, а вільний член – ні) або один розв’язок, що дорівнює .

По-друге, якщо перший коефіцієнт не нульовий, рівняння не вироджене і розв’язується за алгоритмом, відомим з курсу шкільної математики:

• обчислюється дискримінант за формулою ;
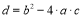• якщо дискримінант від’ємний – коренів немає; якщо нульовий – корінь один і обчислюється за формулою ; якщо дискримінант додатній – коренів два і обчислюються вони за формулами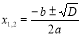

Запишемо фрагмент тексту програми з урахуванням, що якщо коефіцієнт a дорівнює 0, вхідні дані вважаються некоректними:

var a,b,c,x1,x2,d:real;

begin

   write(‘Input numbers  ’);

   readln(a,b,c);

   if (a=0)     {Перевірка коректності вхідних даних}

   then writeln(‘Input error’)

   else begin

         d:=b*b-4*a*c;

         if (d<0)

         then writeln(‘Solution of equation no exist’)

         else if d=0

              then begin

               x1:=-b/(2*a);

               writeln(‘x=’,x:0:3);

              end

              else begin

                    x1:=(-b+sqrt(d))/(2*a);

                    x2:=(-b-sqrt(d))/(2*a);

                    writeln(‘x1=’,x1:0:3);

                    writeln(‘x2=’,x2:0:3);

              end;

   end;

   readln;

end.

Задачі для самостійного розв’язання:

1. Розв'язати лінійне рівнян­ня ах=b.
2. Визначити кількість коренів рівняння .
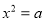3. Скласти програму розв’язку нерівності ах>b, де a, b – будь-які числа.
4. Розв’язати нерівність .
5. Розв’язати нерівність .
6. Два квадратних рівняння задано своїми коефіцієнтами та 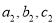. Визначити, чи мають вони однакові пари коренів.
7. Два квадратних рівняння задано своїми коефіцієнтами 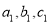та 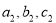. Чи утворюють в сукупності корені обох рівнянь арифметичну прогресію?
8. Два квадратних рівняння задано своїми коефіцієнтами 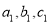та 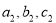. Чи можуть бути корені обох рівнянь сторонами деякого прямокутника?
9. Розв’язати біквадратне рівняння
10. Квадратний багаточлен заданий коефіцієнтами a, b, c, де a0. Визначити, чи корені відповідного рівняння є парними числами.

 

VІIІ категорія. Задачі з шаховою дошкою.

Умова задачі. Дано два числа row та col, що є номером рядка та стовпчика на шаховій дошці. Визначити, якого кольору клітинка з цими координатами.

Розв’язок задачі:

Спочатку визначимося, як задаються координати клітинки шахової дошки. На реальній шаховій дошці рядки нумеруються числами від 1 до 8 , а стовпчики задаються буквами від a до h. Оскільки в програмуванні змішувати різні типи даних досить складно, домовимося, що і рядки, і стовпчики задаються цілими числами від 1 до 8. Таким чином перевірка коректності вхідних даних тут обов’язкова.

Тепер спробуємо проаналізувати колір різних клітинок дошки. Оскільки нижня ліва клітинка з координатами (1,1) біла, то далі білі клітинки першого ряду будуть мати непарні номери стовпчиків. Відповідно клітинки першого ряду з парними номерами стовпчиків будуть чорними. У другому рядочку ситуація протилежна: клітинки з непарними номерами стовпчиків мають чорний колір, а клітинки з парними номерами – білий. Далі картина повторюється.

Підіб’ємо підсумок: рядочки з непарними номерами мають білими клітинки з непарними номерами стовпчиків, а рядочки з парними номерами навпаки. Тобто можна сказати, що у білих клітинок парність номерів рядочків і стовпчиків співпадає.

З усього вище сказаного перевірку клітинки на білий колір можна оформити двома способами:

• перевірка парності номерів рядків та стовпчиків окремо;

(row mod 2 = 0)and(col mod 2 = 0) or (row mod 2 = 1)and(col mod 2 = 1)

• співпадання парності номерів рядків та стовпчиків:

(row mod 2 = col mod 2)

Фрагмент програми має такий вигляд:

var row,col:byte;

begin

   write(‘Input numbers  ’);

   readln(row,col);

   if (row<1)or(row>8)or(col<1)or(col>8)     {Перевірка коректності вхідних даних}

   then writeln(‘Input error’)

   else if row mod 2 = col mod 2

        then writeln(‘White’)

        else writeln(‘Black’);

   readln;

end.

Задачі для самостійного розв’язання:

1.           Поле шахової дошки визначається парою натуральних чисел, кожне з яких не перевищує 8. Перше число – номер стовпчика (при рахунку зліва направо), друге – номер рядка (при рахунку знизу вгору). Дано натуральні числа k, l, m, n, кожне з яких не перевищує восьми. З’ясувати чи є поля (k, l) і (m, n) полями одного кольору.
2.           Поле шахової дошки визначається парою натуральних чисел, кожне з яких не перевищує 8. Перше число – номер стовпчика (при рахунку зліва направо), друге – номер рядка (при рахунку знизу вгору). Дано натуральні числа k, l, m, n, кожне з яких не перевищує восьми. Визначити, чи загрожує полю (m,n) фігура, що розташована на полі (k,l). Фігурою може бути:

• тура;
• слон;
• пішак;
• король;
• ферзь;
• кінь.

Примітка:  1. На горизонталі однаковими є номери рядків, а на вертикалі – номери стовпчиків.

2. Різниця координат клітинок на діагоналі однакова.

  3. Різниця між координатами коня в одному напрямку дорівнює 1, а в іншому 2.

 

IX категорія. Задачі, які потребують для свого розв’язання використання команди вибору.

Умова задачі. Дано натуральне число N , яке визначає вік людини (в роках). Додати до цього числа найменування «рік», «роки» або «років», наприклад 1 рік, 42 роки, 26 років.

Розв’язок задачі:

Після введення числа з клавіатури обов’язкова, як і раніше, перевірка коректності вхідних даних, інакше відповідь може бути отримана неправильна (подумайте чому).

Далі очевидно, що слово, яке дописується до числівника, залежить від останньої цифри числа. Якщо ця цифра «1» – дописується слово «рік», якщо цифри «2» або «3» – дописується слово «роки», в усіх інших випадках – дописується слово «років». Винятком є числа другого десятка, оскільки до них завжди дописується слово «років» незалежно від останньої цифри. Ці числа потрібно перевірити окремо командою умовного переходу.

Відповідь має три варіанти, а тому для наочності має сенс використовувати команду вибору. Зверніть увагу, що оскільки кириличний текст виводиться на консоль некоректно, для виведення застосовується транслітерація.

Фрагмент програми має такий вигляд:

var Year:byte;

begin

   write(‘Input year  ’);

   readln(year);

   if year>100            {Перевірка коректності уведення}

   then writeln(‘Input.error.’)

   else if (year>=10)and(year<=20)

        then writeln(Year,‘  rokiv.’)

        else case Year mod 10 of

              1: writeln(Year,‘  rik.’);

              2..4: writeln(Year,‘  roky.’);

              else writeln(Year,‘  rokiv.’)

            end;

   readln;

end.

Задачі для самостійного розв’язання:

1. Дано натуральне число К. Надрукуйте фразу «Ми знайшли К грибів у лісі», узгодивши слово «гриб» с числом К (1 гриб, 23 гриба, 145 грибів тощо).
2. Написати програму, яка за номером дня тижня виведе на екран кількість уроків у Вашому класі в цей день.
3. Скласти програму, яка за заданим роком і номером місяця визначає кількість днів у цьому місяці.
4. Для кожної введеної цифри (0-9) вивести її назву англійською мовою (0 – zero, 1 – one, 2 – two? ...)
5. Написати програму, яка за номером місяця видає назву наступного за ним місяця.
6. Написати програму, яка за днем тижня виводить на екран його назву (Наприклад, 3 – середа)
7. Скласти програму, яка за даним числом (1 – 12) виводить назву відповідного йому місяця.
8. Написати програму, яка за введеним номером пори року видає відповідні цій порі місяці та кількість днів у кожному з місяців.
9. Скласти програму, яка виведе словесний опис шкільних оцінок (1..3 – незадовільно, 4..6 – задовільно, 7..9 – добре, 10..12 – відмінно).
10. Нехай властивостями кола є радіус (перша властивість), діаметр (друга властивість) і довжина окружності (третя властивість). Скласти програму, яка за номером властивості запитувала би його відповідне значення і обчислювала б площу кола.
11. Написати програму, яка б за введеним номером одиниць виміру (1 – дециметр, 2 – кілометр, 3 – метр, 4 – міліметр, 5 – сантиметр) і довжині відрізка L, яка уводиться у сантиметрах, видавала б відповідне значення довжини відрізка в метрах.
12. Написати програму, яка за введеним числом від 1 до 11 (номером класу) видає відповідне повідомлення «Привіт, K-класник!». Наприклад, якщо К=1, «Привіт, першокласник!», при К=4: «Привіт, чотирикласник!».
13. Написати програму, яка за даним натуральним числом від 1 до 12 (номером місяця) видає усі святкові дні у цьому місяці.
14. Дано два дійсних додатних числа. Арифметичні дії над числами пронумеровані (1 – додавання, 2 – віднімання, 3 – множення, 4 – ділення). Скласти програму, яка за введеним номером виконує ту або іншу дію над числами.
15. Написати програму, яка б за введеним номером одиниці виміру (1 – кілограм, 2 – міліграм, 3 – грам, 4 – тонна, 5 – центнер) і масі М у цих одиницях виміру виводила б задану масу в кілограмах.
16. Існує пронумерований список деталей: 1 – шуруп, 2 – гайка, 3 – вінт, 4 – цвях, 5 – болт. Скласти програму, яка по номеру деталі виводить на екран її назву.
17. За даним порядковим номером 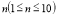вивести на екран прізвище учня вашого класу з класного журналу.
18. Щоб бути завжди чистою, людині необхідно х шматків мила на рік. Якщо мити лише п’яти, то мила знадобиться у 12 разів менше, а тільки вуха – ще на один шматок менше. Скласти програму, яка б за вибором користувача давала відповідь, яку кількість шматків мила необхідно закупити на n років вперед, щоб: а) митися повністю; б) мити лише вуха; в) мити лише п’яти; г) мити п’яти і вуха.
19. Розробити алгоритм-лотерею, який, використовуючи уведене користувачем ціле число в діапазоні від 1 до 6, визначатиме призи:
    •     комп’ютер,
    •     принтер,
    •     сканер,
    •     компакт-диск,
    •     флеш-пам’ять,
    •     колонки.
20. Розробити програму-довідник, яка за введеним значенням радіуса R пропонуватиме користувачу послуги в обчисленні:

1 – довжини кола;

2 – площі круга;

3 – об’єму кулі;

4 – площі поверхні кулі.

21. За віком людини визначить назву періоду життя (раннє дитинство, дитинство, отроцтво, юність, молодість, зрілість, похилий вік, старість).
22. Розробити програму виведення на екран номера кварталу, до якого відноситься місяць, заданий числом від 1 до 12 (січень, лютий, березень – 1 квартал і т.д.).
23. Дано ціле число n і дійсне число x. За введеним значенням змінної n, яке визначає порядковий номер функції, визначити:

1) sinx;

2) cosx;

3) tgx.

24. Дано ціле число n 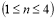, яке визначає порядковий номер кварталу року (січень, лютий, березень – 1 квартал і т.д.). За вказаним значенням n вивести перелік місяців, які відносяться до даного кварталу.
25. Розробити програму, яка за введеною датою народження людини визначатиме, до якого знаку Зодіака вона належить:

20.01 – 18.02 – Водолій

19.02 – 20.03 – Риби

21.03 – 19.04 – Овен

20.04 – 20.05 – Телець

21.05 – 21.06 – Близнюки

22.06 – 22.07 – Рак

23.07 – 22.08 – Лев

23.08 – 22.09 – Діва

23.09 – 22.10 – Терези

23.10 – 22.11 – Скорпіон

23.11 – 21.12 – Стрілець

22.12 – 18.01 – Козерог