Відкритий урок "Властивості степеня з натуральним показником"

Властивості  степеня  з натуральним показником

Мета: систематизувати знання властивостей степеня з натуральним показником, удосконалити вміння використовувати властивості степенів для розв’язування задач, формувати навички усних розрахунків; розвивати пам’ять, виховувати почуття поваги до предмета.

Тип уроку:  удосконалення вмінь і навичок учнів.

Очікувані  результати:

Після  цього  уроку  учні  зможуть:

• застосовувати  властивості  степеня  з  натуральним  показником  при  спрощенні  виразів;
• користуватися  властивостями  степеня  при  визначенні  значень  числових  виразів  та  при  порівнянні  чисел;
• застосовувати  властивості  степеня  з  натуральним  показником  під  час  виконання  самостійної  роботи.

Методи:   словесні (еврістична  бесіда,  пояснення); наочні  (опорні  таблиці, картки); практичні  (усні  і  письмові  вправи, самостійна  робота);  метод  повторення,  поступового  ускладнення  завдань; методи, спрямовані  на  розвиток  критичного  мислення (аналіз, висновки, самооцінка); методи  заохочення  (диференційоване домашнє завдання);  методи перевірки (фронтальні  опитування,  самостійна  робота).

Обладнання:  дошка,  «алгебраїчна  ромашка»,  роздатковий матеріал, плакати «Застосування степеня числа у різних галузях», О.С.Істер підручник Алгебра, 7 клас, 2015.

Хід  уроку

І. Організаційно  психологічний  етап.

Вітання  з  учнями.

-   Я  хочу  розпочати  сьогоднішній  урок  із  питання,  яке,  здається,  недоречним  на  уроці  математики: „Як  ви  гадаєте,  чи  знають  дорослі  люди  та  діти  шкільного  віку  елементарні  правила  дорожнього  руху?”

Ймовірна  відповідь: „Так!”

       -  А  чи  всі  користуються  ними,  тобто  чи  всі  застосовують  правила  дорожнього  руху  у  реальних  життєвих  ситуаціях?

          Ймовірна  відповідь: „Ні!”

Нажаль,  таких  прикладів  можна  навести  чимало.  Ми  знаємо  правила,  чули  про  закони,  але  користуватися  ними  не  вміємо або  користуємося  невдало.  В  математиці,  як  у  житті!  Вивчив  правило – чудово,  а  чи  навчився  ним  користуватися?    Ми  з  вами  на  минулих  уроках познайомились з властивостями  степеня  з  натуральним  показником,  виходячи  з  цього,  як  ви  гадаєте,  чому  ми  маємо  присвятити  свій  сьогоднішній  урок?

Ймовірна  відповідь: „Тому,  щоб  навчитися  користуватися  вивченими  властивостями  степеня  на  практиці.”

-  Дійсно,  на  сьогоднішньому  уроці  ми  маємо  навчитися  застосовувати  властивості  степеня  на  практиці.

ІІ. Перевірка домашнього завдання.

  Тож  до  роботи!  Вдома  кожен  з  вас  мав  навчитися  формулювати    властивості  степеня  з  натуральним  показником  і  записувати  їх  у  вигляді  формул. 

(Біля дошки один учень пише формулу, другий – справа відповідний                                приклад, діти з місця формулюють правила).

Запис на  дошці:      

Властивості  степеня  з  натуральним  показником:

1.          a^m ∙ aⁿ =
2.          a^m : aⁿ =       а ≠ 0,  m > n
3.          (a^m)ⁿ =
4.          (ab)ⁿ =
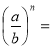5.                b ≠ 0

Учитель  підводить  підсумки  роботи  учнів:  узагальнює,  перевіряє,  схвалює.

-  Отже,  теорію  ви  вивчили  чудово.  Подивимось  як  ви  впорались  із  практичною  частиною  домашнього  завдання. 

Перевірка завдання №118 та №123

А ще я  запропонувала  вам  намалювати  „алгебраїчні  ромашки”  (на дошці  намальована  „алгебраїчна  ромашка”)  і,  користуючись  різними  властивостями  степеня,  на  пелюстках  цих  „ромашок”  написати  приклади,  які  б  дорівнювали  виразу  в  середині.  Чим  більше  пелюсток,  тим  краще.  Покажіть  свої  „ромашки”!  Давайте  разом  заповнимо  пелюстки  моєї  „алгебраїчної  ромашки”.

                (Учні  пропонують  свої  варіанти  прикладів,  учитель  вписує  їх  у  пелюстки  „алгебраїчної  ромашки”,  корегує  приклади  і  правильність    математичного  мовлення  учнів,  якщо  це  потрібно. Учні приклеюють свої ромашки навколо ромашки вчителя)

ІІІ. Екскурс  в історію
      Запишіть відповідь у вигляді степеня з основою с і ви дізнаєтеся прізвище та ім'я великого французького математика.

Ключ:

Відповідь: Рене Декарт.

Так, це великий французький математик Рене Декарт, який першим ввів поняття степеня числа. Головним відкриттям Декарта в математиці переважна більшість вчених вважає легендарну систему координат, яка дістала згодом назву декартова. Ця система зіграла визначну роль в історії аналітичної геометрії. Знаменитий філософ, природознавець і математик Рене Декарт придумав нумерацію крісел в театрах. Запропонована ним система швидко прижилася, і зараз вона нікого не дивує.
          А взагалі слово Exponent, яке ввів для показника степеня Штифель в 1553році  означає «показник»,  «позивач». А Декарт до науки ввів показники степеня в сьогоднішньому вигляді  у 1637. Англієць за народженням, що жив у Франції, Юг писав 5а^IV ,  Ерігон – 5а4,  у Декарта ці символи перетворились в 5а⁴. Вираз «піднесення до степеня» вперше  з’явився в 1716 році в роботі  «Mathematische Lexicon» Вольфа.

Поняття степеня виникло в далекій давнині. Упродовж багатьох століть розвиток науки дуже гальмувався, тому що науковцям довго не вдавалося ввести у сої дослідження доречні позначення. Тому виклад наукових робіт мав громіздкий вигляд.

Степінь числа використовують, коли мають справу, як із дуже великими, так і дуже маленькими числами.

Степінь у географії

      Степінь у біології

      Степінь числа у астрономії

      Степінь числа у фізиці

      Степінь числа у хімії

     Степінь числа у економіці

Звернути увагу учнів на слова М.В.Ломоносова

"Нехай хтось спробує викреслити з математики степені, і він буде бачити,

що без них далеко не заїдеш"

ІV. Систематизація знань

1. Усна робота « Мікрофон»

   (-1)² =                      -1¹²⁶ =

    -1² =                          (-1 )¹²⁶ =

   (-1)³ =                       -2² =

    -1³ =                          2² =

   (-1 )⁵ =                      (-2)² =

   (-1 )²⁵ =                    -2³ =

   (-1 )¹²⁵ =                   2⁵ =

2.Завдання на знаходження помилки. Гра «Неуважний учень»
          Виконуючи завдання на  перетворення виразів зі степеннями, неуважний учень припустився деяких помилок. Виправте помилки та поясніть, які означення, властивості та правила не знає учень.

Запис на дошці

3. Робота за заготовленими заздалегідь завданнями.

Замість * вставте потрібне число:

    (с³) ^* =с¹²

а¹⁶ а ^* =а³²

(у^*)⁵= у¹⁰

х^*: х² = х⁷

(5у^*)³= 125у⁶.

4. Відпочинок на уроці

Відомий французький письменник ХІХ ст. Анатоль Франс одного разу зауважив: «Навчатися можна тільки весело… Щоб перетравлювати знання, потрібно споживати їх з апетитом». А Блез Паскаль, видатний французький філософ , математик і фізик ХVII ст., сказав: «Предмет математики настільки серйозний, що корисно не нехтувати нагодами робити його трохи цікавішим» .

Відпочинок — це зміна дії.

 Відпочинок — це проведення деякого часу без звичних занять.

(За тлумачним словником)

Гра «Віриш — не віриш»

Чи вірите ви, що...

1. Існує геометрія, у якій паралельні пере­тинаються? (Так. Це проективна геометрія)
2. Л. М. Толстой порівнював людину зі зви­чайним дробом? (Це дійсно так, він порівнював людину з дробом, чисельником якого є те, що вона собою являє насправді, а знаменником–те,що вона про себе думає. Чим краще людина про себе думає,тим більший знаменник, а отже, тим менший дріб. Подумайте про це порівняння і зробіть висновки.)
3. Якщо покласти людину на спину з роз­простертими руками і ногами, то кінчики пальців рук і ніг опиняться на колі, центр якого — пуп? (Так)
4. У Франції не дуже давно жила родина, яка не мала прізвища. Замість нього вона носила набір цифр (Так. Набір цифр – 1792. Останній представник цього роду помер 1904 року)
5. Якщо ви помітили, багато римських чисел легко викласти з паличок. Це підтверджує гіпотезу, що римські числа насправді придумали китайці, які їдять паличками (Ні)
6. Дуже багато марновірств пов’язано із числом 13. У Парижі існували фірми з доставки чотирнадцятого, якщо десь за обідом збиралося 13 людей.(Так)
7. Серед простих чисел немає таких, які йдуть у натуральному ряді одне за одним.(Ні, є:2 і 3)
8. У Китаї, де вперше виникли від’ємні числа, їх позначали чорним кольором на відміну від додатних, які писали червоним. (Так)
9. Існує число, якому поставили пам’ятник. (Так, пам’ятник нулю в Будапешті та пам’ятник числу π в Сіетлі на східцях перед будівлею Музею мистейцтв)

5.Робота з підручником

№124 (1ст. – з поясненням біля дошки, 2ст. – самостійно)

№125 (1,2 – з поясненням біля дошки, 3 – самостійно)

№126 (2 – з поясненням біля дошки, 1 – самостійно)

V.  Підведення  підсумків  уроку

-  А  зараз  нам  лишається  підвести  підсумки  роботи  на  уроці.  По-перше,  дозвольте  оцінити  роботу  окремих  учнів,  тобто  їх  рівень  навчальних  досягнень. 

(Учитель  озвучує  і  коментує  оцінки  учнів,  які  активно  працювали  протягом  уроку)

-  По-друге,  пропоную  повернутися  до  проблеми,  яку  ми  підняли  на  початку  уроку: „Чи  досить  у  навчанні,  у  роботі,  у  житті  лише  знати  певні  правила,  закони  чи  властивості?  До  яких  висновків  ви  дійшли?”

(Ймовірна  відповідь:  Ні,  недостатньо  вивчити  правила  чи  формули,  треба  навчитися  ними  користуватися,  тобто  застосовувати  на  практиці!)

-  Дійсно,  і  це  твердження  стосується  не  тільки  математики,  а  й  правил  громадської  поведінки,  правил  дорожнього  руху,  конституційних  або  юридичних  законів.  Отже,  навчаючись  користуватися  своїми  знаннями,  ми  зростаємо  як  особистість,  ми  набуваємо  досвіду  і  впевненості  у  своїх  силах,  ми  просуваємось  вперед,  готуючись  до  дорослого  життя!

Я вважаю, що ви добре працювали і приймали активну участь на уроці. А закінчити урок я хочу словами Норберта Вінекра «Математика – наука молодих. Інакше й не може бути. Заняття математикою – це така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості». Я сподіваюсь, що сьогоднішній урок став для вас хорошим тренування.