Віртуальний довідник "Функції. Властивості функцій"
![]()
Загальний вид функцП Зростання та спадання
![]()
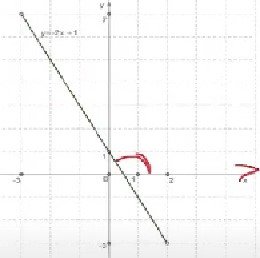
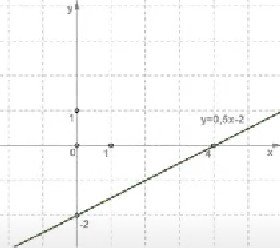 Значення К
Значення К
Якщп К>О, тпд( лјн(йна функцјя зрагтае; якща К < а, T04i I1iHi7F-ra спадые.
|
|
|
|
|
|
|
е парною |
е непарною |
|
е спадною |
е зростаючою |
Значення Ь
Ь - це џрдинетв точки перетину графАе з ВЈКСЮ орди ват.
тупи7 кут з непрямим Bici ах гострий кут з додатнјм напряном вјсј о
спадаЕ зростаЕ
Яку властивјсть (3 наведених мас функцЈя у![]()
На одному з наведених pvjcyHki3 зображено ескЈз графјка функцј[ у = 2х+ 3 ![]()
![]() цей рисунпес
цей рисунпес
|
iiiiiiiii
|
Пряма
![]()
![]() Загальний вид прямо7
Загальний вид прямо7![]()
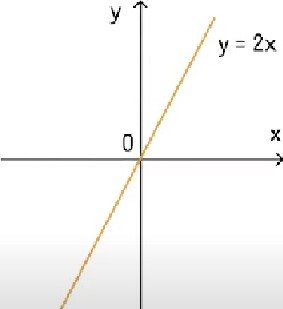
У = КХ
ГрафП« прямоћ п ![]() завжди проходить через початок координат.
завжди проходить через початок координат.
Укажђть рисунок, на якому зображено ескјз графЈка функцЈЈ у kr при К > 1.

Квадратична
функц'я виду:
|
|
У = ах2 |
+ с |
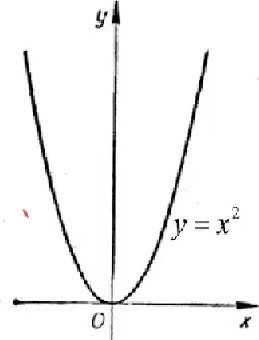
![]() квадратично1 функци - парабола.
квадратично1 функци - парабола.
Квадратична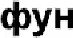
![]()
![]() Загальний здглпд квадратично] функцГ7
Загальний здглпд квадратично] функцГ7
У =дх 2 +bx+c
![]()
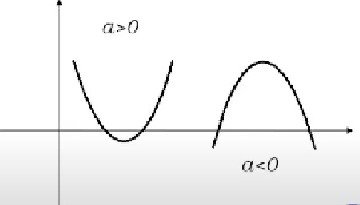
![]() а > 0, то парабола напрямлена вгору
а > 0, то парабола напрямлена вгору ![]() якщо а < 0, то вниз
якщо а < 0, то вниз
![]()
![]() координату вершини параболи
координату вершини параболи
 -е + 4х-6=0
-е + 4х-6=0
Вершина параболи
![]()
[ЦОЕ зн,1Ати кг.лрщиь-ыти вершини у ![]() найпростјше преста пјдстзвити а5счле„•
найпростјше преста пјдстзвити а5счле„•
2. перлини у функц'лл ан,лйти у.
![]()

|
|
|
функцјя модуля
ВластивостЈ![]()
|
|
|
|
|
х |
![]() даноТ функцјт Е бјсектрисою [ i l l
даноТ функцјт Е бјсектрисою [ i l l
HBepTi
Кут двома частичами прямий.
![]() дана функцјя е пгрною.
дана функцјя е пгрною.
![]()
Укаж\ть парну функцЈю.
![]()
|
|
|
в |
|
|
д |
|
|
|
|
у |
tg:r |
|

Загальний вигляд ![]()
к
 де К -
де К - ![]()
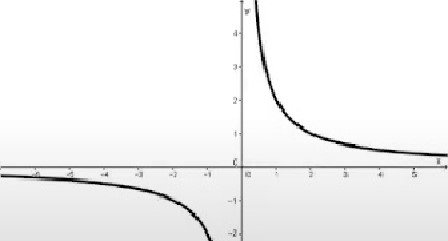
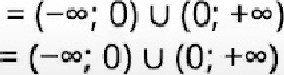 1.
1. ![]() Е непарною
Е непарною
2, Графћк нЈколи не перетина€ ![]() Bici з,
Bici з, ![]() 4.
4. ![]()

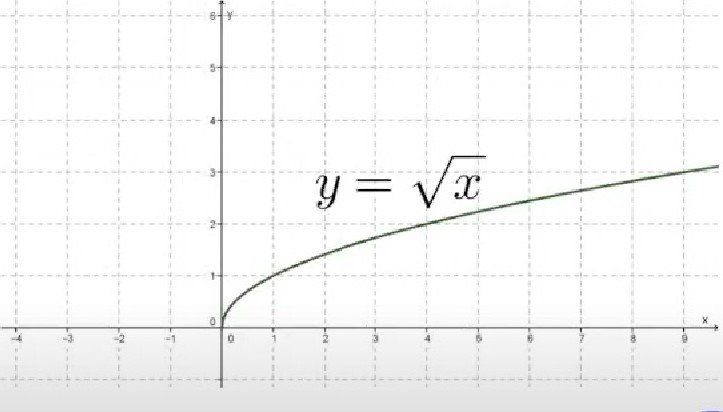 1 . Область визначення функцй“ —
1 . Область визначення функцй“ —![]()
2. Нуль функцй' у = 0, якщо х = 0
З. ![]() зроста€ на промјжку [О;+ф)
зроста€ на промјжку [О;+ф) ![]() функцй•
функцй•
Показникова 
Показникова ![]() - функця, де залежна змЈнна
- функця, де залежна змЈнна
(х) знаходитњся в показчику![]()
у = ах,а > 0, а * 1
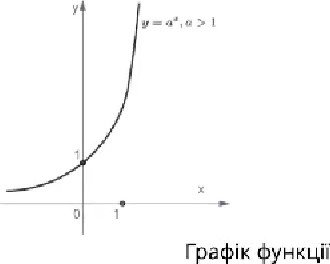 зддджить вјд иснсви а
зддджить вјд иснсви а
![]() 2
2
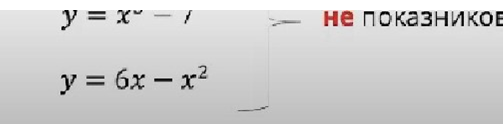
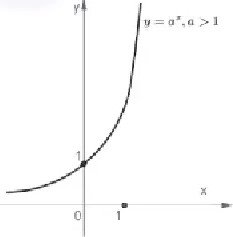 не покгзнлковј фунщГГ
не покгзнлковј фунщГГ
![]() Область визначення (всг допустив множина чисел (—т„ +x).
Область визначення (всг допустив множина чисел (—т„ +x).
2. Область значень (3Ci ![]() зн множина scix додатних д'йснлх чис
зн множина scix додатних д'йснлх чис
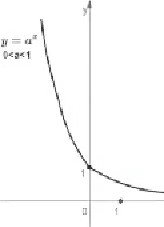
З. Якще а > 1, зростаЕ.
4, Якщо О < 1, функцЈя спадае


![]() -
- ![]() виду:
виду:![]()
У = loga х

![]() у = sin х
у = sin х
область визначення
|
-4 |
|
|
|
|
![]() множина значень
множина значень
Е (sin х)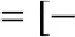
napHicTb/HenapHicTb ![]() непарна, 60 sin(—x) — — —sinx
непарна, 60 sin(—x) — — —sinx
До кожного початку речения (1—3) його saki1fMeHHA (А— Д) так, щоб утво„ рилося правильне твердркення![]()
|
|
Почоток речення |
|
Загсјнченнд речення |
|
1 |
Функщя у = logo,$ х |
А |
не визначена при х = 1. |
|
2 |
Футгкщя у — sin х |
Б |
набувае |
|
З |
Функщя У = 2х 2 |
В |
с непарною. |
 Г мае лише одну точку локального екстремуму, Д зростае на промигку (0;
Г мае лише одну точку локального екстремуму, Д зростае на промигку (0;![]()
 у — cos х
у — cos х
|
|
У=спзх
|
|
|
|
||
|
|
|
|

Властивост' функцп• у cos х
cos х
|
|
У—сом |
|
|
|
Обла«;ть визначення
D(cosx) = IR
Множина значень
E(cos х) — 1; 11
![]() функц[)': парна, бо
функц[)': парна, бо ![]() —— cosx
—— cosx
![]()
Асимптоти графП«а  у — tg х
у — tg х
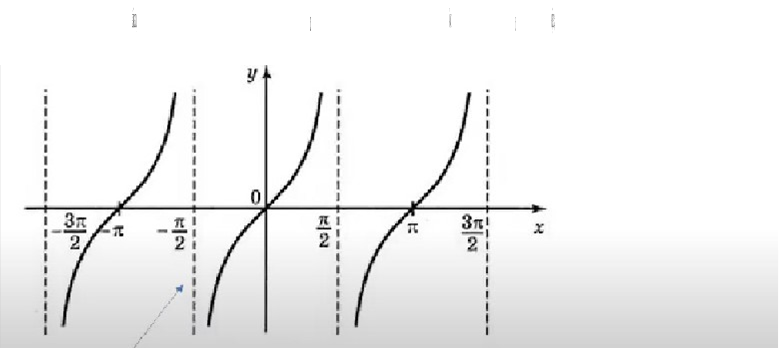
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 Асимптоти граф1ка - до яких значення
Асимптоти граф1ка - до яких значення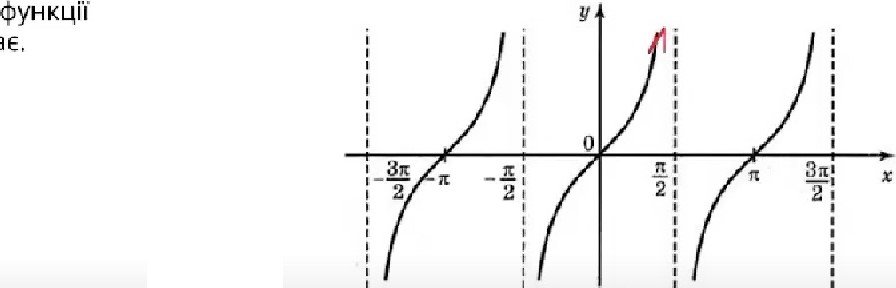
|
|
|
|
|
2 |
2, |
33 • Т, |
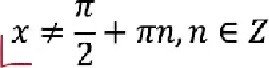 Область визначення
Область визначення
Множина значень
E(tgx) = 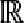
|
gx |
|
|
![]() непарна, бо
непарна, бо ![]() = —tgx х + п =t
= —tgx х + п =t
|
Установоть вщповщн'сть востями (А — Д). Функщя 2 з у = tg х |
функц'ями„ Б В д |
заданиии формулами ( 1 —4), та ТхнЈми власти- Властиветь функц»• областю визначення функцй е промђ;кок функтпя спадае на (0; + ос) функцт зростас на АнтервалЈ + х) парна функцо
|
|
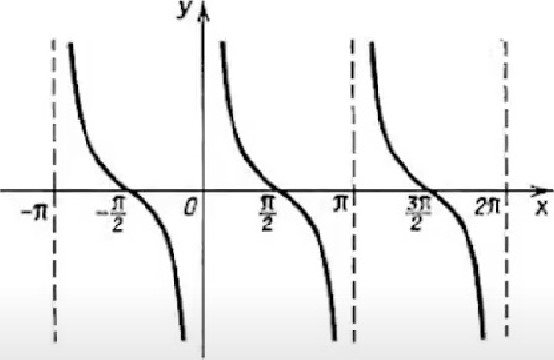
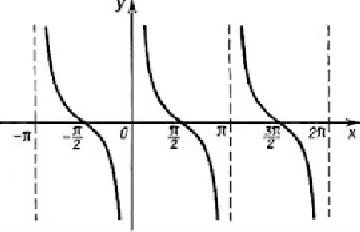
 у = ctg х
у = ctg х ![]() функцП у = сед х
функцП у = сед х
|
Т = ctg(x + п) = ctgx |
![]() Область визначення
Область визначення
множина значень
E(ctgx) = 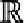
![]() непарна, 60 ctg(—x) = —ctgx
непарна, 60 ctg(—x) = —ctgx
крива - котангенсоТда
 Уетгьюв'ть атпемднбеть мЈы функцьами
Уетгьюв'ть атпемднбеть мЈы функцьами 
Установпь в\дповщнють мок функц'ями, заданими формулами (Л ![]() властивостями (А
властивостями (А![]()
Функщя
у cosx 2 у = ctg х
з![]()
 |
4
Властивють функцп
областю визначення функц'ђ“ с![]()
Б областю значень функц'л е Bwpi30k 1; ![]()
в функци спадае на јнтервал' + т)
Г непарна![]()


про публікацію авторської розробки
Додати розробку








