Властивості арифметичного квадратного кореня. Тотожність √(a^2 )=|a|
1
Тема: Властивості арифметичного квадратного кореня. Тотожність ![]()
Мета:
навчальна: сформувати в учнів знання про властивості арифметичного квадратного кореня, сформульовані у вигляді теорем; формувати вміння застосовувати вивчені властивості для обчислення значень виразів, спрощення та перетворення виразів; формувати культуру усних та письмових обчислень;
розвивальна: формування компетентності вміння вчитися впродовж життя (формування уміння визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети; знаходити зв’язок з раніше вивченим: переносити набуті знання в нові ситуації); стимулювання учнів до висловлювань без побоювань помилитися; формування компетентності спілкування державною мовою (формування умінь ставити запитання і розпізнавати проблему; міркувати, робити висновки; грамотно висловлюватися рідною мовою);
виховна: формування соціальної і громадянської компетентності (уміння висловлювати власну думку, слухати і чути інших, оцінювати аргументи та змінювати думку на основі доказів); формування компетентності ініціативності та підприємливості (формувати уміння вирішувати життєві проблеми, аналізувати, прогнозувати).
Тип уроку: засвоєння нових знань
Обладнання: конспект уроку, підручник, сканер QR-коду, презентація до уроку, роздатковий матеріал.
Підручник: Істер О.С. Алгебра: підруч. для 8-го кл. загальноовіт.закл./ О.С.Істер. – Київ: Генеза, 2016. – 272с.
Хід уроку
І. Організаційний момент.
Добрий день. Я рада всіх Вас вітати на уроці.
ІІ. Підготовка до сприйняття матеріалу або актуалізація опорних знань, умінь, уявлень та чуттєвого досвіду.
На попередніх уроках ви навчилися добувати арифметичний квадратний корінь із числа, вивчили поняття арифметичного квадратного кореня.
А сьогодні на уроці, я сподіваюсь, що слова відомого французького математика Рене Декарта «Мало мати хороший розум, головне добре його застосовувати» будуть реалізовані на повну силу.

ІІІ. Актуалізація опорних знань
Розпочнемо з розминки для нашого розуму, щоб налаштувати його на серйозну роботу. Дайте відповіді на наступні запитання:
-
Що називають квадратним коренем з числа
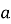 ?
?
Квадратним коренем із числа ![]() називають число, квадрат якого дорівнює
називають число, квадрат якого дорівнює ![]() .
.
-
Що називають арифметичним квадратним коренем із числа
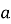 ?
?
Арифметичним квадратним коренем із числа а називають таке невід’ємне число, квадрат якого дорівнює а?
-
При яких значеннях
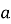 вираз
вираз 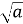 не має змісту?
не має змісту?
Вираз ![]() не має змісту, якщо
не має змісту, якщо ![]()
-
Чи має корені рівняння
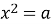 , якщо
, якщо 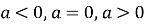 , і якщо має, то скільки?
, і якщо має, то скільки?

Працюємо з наступними завданнями усно:
- Обчисліть
![]() ,
, ![]() ,
,![]() ,
, ![]() ,
, ![]() .
.
- Знайдіть значення виразу:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
- Розв’яжіть рівняння:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

ІV. Мотивація навчальної діяльності.
На фізиці Ви дізнаєтесь, що швидкість, з якою тіло рухається навколо Землі по колу радіуса ![]() під дією сили всесвітнього тяжіння, можна обчислити за формулою
під дією сили всесвітнього тяжіння, можна обчислити за формулою ![]() , де
, де ![]() – гравітаційна стала,
– гравітаційна стала, ![]() – маса Землі,
– маса Землі, ![]() – радіус Землі. Для визначення цієї швидкості можна обчислити підкореневий вираз, а потім добути корінь. А можна зробити інакше: окремо добути корені з величин
– радіус Землі. Для визначення цієї швидкості можна обчислити підкореневий вираз, а потім добути корінь. А можна зробити інакше: окремо добути корені з величин ![]() та скористатися правилом знаходження кореня з добутку і частки. Проаналізувавши різні варіанти порядку дій, можна вибрати оптимальний спосіб обчислення значення даного виразу.
та скористатися правилом знаходження кореня з добутку і частки. Проаналізувавши різні варіанти порядку дій, можна вибрати оптимальний спосіб обчислення значення даного виразу.

V. Оголошення теми, мети і завдань уроку.
Отже, ми сьогодні з Вами ознайомемось з властивостями арифметичного квадратного кореня, а саме дізнаємось як добувати квадратний корінь із добутку, дробу та квадратний корінь з квадрата та зі степеня.
Розгорніть Ваші зошити та запишіть дату та тему сьогоднішнього уроку:
Двадцять сьоме грудня
Класна робота
Властивості арифметичного квадратного кореня. Тотожність ![]()
VІ. Вивчення нового матеріалу
Перейдемо до вивчення нового матеріалу
Порівняємо значення виразів ![]() і
і ![]() . Обчислимо значення кожного із виразів:
. Обчислимо значення кожного із виразів:
![]()
![]()
Маємо, що ![]() =
= ![]() , тобто корінь із добутку двох чисел дорівнює добутку їх коренів. Така властивість справджується для добутку будь-яких двох невід’ємних чисел.
, тобто корінь із добутку двох чисел дорівнює добутку їх коренів. Така властивість справджується для добутку будь-яких двох невід’ємних чисел.
Теорема 1 (про корінь із добутку). Корінь із добутку двох невід’ємних чисел дорівнює добутку коренів із цих чисел, тобто якщо ![]() то
то
![]()
Дана теорема справедлива коли множників під знаком кореня три і більше.
Вираз ![]() має зміст за умови, якщо
має зміст за умови, якщо ![]() . Тобто коли змінні
. Тобто коли змінні ![]() і
і ![]() – одного знака, в значить і тоді, коли змінні
– одного знака, в значить і тоді, коли змінні ![]() і
і ![]() одночасно набувають від’ємних значень, то
одночасно набувають від’ємних значень, то ![]() , де
, де ![]() . Отже, наступна рівність є ключовою
. Отже, наступна рівність є ключовою
![]() , де
, де ![]() , тобто
, тобто ![]() або
або ![]() .
.
Якщо в рівності ![]() поміняти місцями ліву і праву частини, то одержимо твердження, обернене до теореми 1.
поміняти місцями ліву і праву частини, то одержимо твердження, обернене до теореми 1.

Розглянемо квадратний корінь з дробу.
Теорема 2 (про корінь з дробу). Корінь з дробу, чисельник якого є невід’ємним числом, а знаменним додатним, дорівнює кореню з чисельника, поділеному на корінь із знаменника, тобто, якщо ![]() , то
, то
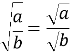
Дану тотожність можна записати і так:
![]() , де
, де ![]() ,
, ![]() .
.
Якщо в рівності ![]() поміняти місцями ліву і праву частини, то одержимо твердження, обернене до теореми 2.
поміняти місцями ліву і праву частини, то одержимо твердження, обернене до теореми 2.

Розглянемо задачу: Для обладнання автостоянки виділили земельну ділянку, що має форму прямокутного трикутника з катетами по 18 м. Визначте відстань між точками А і В.
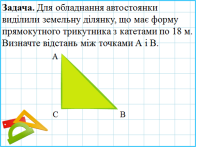
Розв’язання: Відстань між точками А і В є довжиною гіпотенузи прямокутного трикутника АВС. З курсу геометрії Вам відома теорема Піфагора, сформулюйте її.
Скориставшись даною теоремою, запишемо ![]() . Зведемо подібні доданки, отримаємо
. Зведемо подібні доданки, отримаємо ![]() . Щоб обчислити значення цього виразу, слід знати, як знаходити корінь із добутку та корінь з квадрата.
. Щоб обчислити значення цього виразу, слід знати, як знаходити корінь із добутку та корінь з квадрата.
Розглянемо це у наступній теоремі.
Теорема 3 (про корінь з квадрата). Для будь-якого значення ![]() справджується рівність
справджується рівність ![]() .
.
Слід пригадати, що розкриття модуля залежить від знака під модульного виразу.
Ми можемо закінчити знаходити значення виразу ![]()
![]() (м)
(м)
Якщо в нас добувається квадратний корінь не з квадрата, а із степеня, то стверджується наступна теорема.
Теорема 4 (про корінь із степеня). Для будь-якого значення ![]() і натурального числа
і натурального числа ![]() справджується рівність
справджується рівність ![]() .
.

Попрацювавши – відпочинемо з користю та дізнаємось, коли відзначають день квадратного кореня.
День квадратного кореня відзначають в день, коли і число, і порядковий номер місяця є квадратними коренями з числа, утвореного двома останніми цифрами року. Виявилось, що проміжок між святами у роках становить послідовність непарних чисел 3, 5, 7, …. Уперше це свято відзначали 9 вересня 1981 року. Спробуйте вдома і ви визначити найближчий день квадратного кореня.

VІІ. Осмислення нових знань.
1. Інтерактивна вправа. Тест «Властивості арифметичного квадратного кореня»
А зараз перевіримо засвоєння теоретичного матеріалу на практиці: проведемо огляд практичних вправ на закріплення основних властивостей із даної теми. Для цього виконаємо інтерактивну вправу за допомогою інтернет-сервісу LerningApps. Учні першого ряду по черзі виконують вправу біля дошки, інші – за допомогою QR-коду виконують на своєму робочому місці.

2. Робота з підручником.
Вивчивши теоретичний матеріал, із даної теми, запишемо письмові завдання із підручника.
У вас на столах лежать кольорові листочки з чотирма рівнями складності. Ви вибираєте один із листків та виконуєте завдання із підручника, яке ви обрали. До дошки підуть три учні: початкового, середнього та достатнього рівнів та запишуть відповідні розв’язання. Учні із високого рівня виконають самоперевірку.
Початковий рівень
№ 615(1), 617(1)
Середній рівень
№ 625(1), 627(1)
Достатній рівень
№ 633(3), 635(6)
Високий рівень
№ 644(1), 645(3)

Початковий рівень
№ 615(1)
![]() =5
=5![]() 3=15
3=15
№ 617(1)
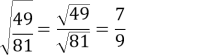
Середній рівень
№ 625(1)
![]()
№ 627(1)
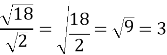
Достатній рівень
№ 633(3)
![]()
№ 635(5)
![]()
Високий рівень
№ 644(1), 645(3)
№644(1)
![]() , якщо
, якщо ![]()
№645(3)
Якщо ![]() , то
, то ![]()

3. Завдання із ЗНО.
А зараз колективно виконаємо завдання із ЗНО-2021 за посібником Олександра Семеновича Істера, а саме завдання відкритої форми з короткою відповіддю.
Знайдіть значення виразу:
![]()
![]()
Отже, відповідь записуємо у вигляді
|
|
|
|
|
|
|
|
|
VIІI. Підведення підсумків уроку.
Підіб’ємо підсумки нашого уроку. Отже, сьогодні на уроці ми ознайомились з властивостями арифметичного квадратного кореня, дізнались як добувати квадратний корінь із добутку, дробу та квадратний корінь з квадрата та зі степеня. Це тільки одна із тем математики, але об’єм математичних знань безкінечний, самі математичні знання неоцінені, а області застосувань математики безмежні.
Тож, я впевнена, що вам сьогоднішній урок буде в нагоді «Так – ні». Якщо Ваша відповідь «Так» записуємо цифру «1», якщо ж «Ні», то цифру «0».
Графічний диктант «Так – ні»
-
Чи є справедливою тотожність
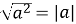 ? (Так)
? (Так)
-
Чи може значення виразу
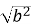 бути від’ємним? (Ні)
бути від’ємним? (Ні)
- Чи є помилка у ланцюжку дій:
![]() (Так)
(Так)
-
Чи правильна тотожність:
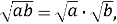 якщо
якщо 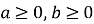 ? (Так)
? (Так)
- Чи справедлива теорема про корінь із добутку для довільної кількості невід’ємних множників? (Так)
-
Чи вірно знайдено значення виразу
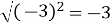 ? (Ні)
? (Ні)
Ключ до графічного диктанту «Так – ні»
![]()
Виконавши самоперевірку та продемонструйте за допомогою цеглинок Lego ваш результат, підніміть вгору ту кількість цеглинок, скільки правильних відповідей ви отримали.

Учні Якубовський Олександр, Котовська Каріна, Замолінський Ростислав підійть по черзі зі своїми щоденниками до мене для оцінювання активності на уроці.
ІХ. Повідомлення та пояснення домашнього завдання.
Підручник: Істер О.С. Алгебра: підруч. для 8-го кл. загальноовіт.закл./ О.С.Істер. – Київ: Генеза, 2016. – 272с.
Вивчити: § 17 (с.137)
Письмово:
Початковий рівень: № 616(1,3), 618(1,4)
Середній рівень: № 626(4,5), 628(1,4)
Достатній рівень: № 634(3), 636(1,6)
Високий рівень: № 646(2), 648(1), 648(2)(дод.)
Додаткове завдання (творче завдання):
Не дивлячись на те, що ми маємо відмінності, ми є доньками і синами наших родин. Навчаємось в одному класі, є мешканцями одного села, є громадянами однієї країни. Тому я пропоную Вам написати твір-есе на тему:
У чому ми рівні та в чому ми різні як учні класу, як члени родини, як жителі України?

При виході з класу, візьміть стікер із долонькою та приклейте так, як ви оцінюєте вашу роботу на уроці. Якщо вам було зрозуміле пояснення нового матеріалу приклейте стікер пальчиком вгору, якщо виникли труднощі – пальчиком вниз.


про публікацію авторської розробки
Додати розробку
