Задачі для тренування при підготовці до олімпіад з фізики

Задачі для підготовки до олімпіад з фізики

Задача 1.  За графіком залежності переміщення від часу, що складається з двох ділянок парабол побудувати графік залежності швидкості, прискорення і шляху від часу руху тіла. Пояснити  рух тіла на кожній ділянці.

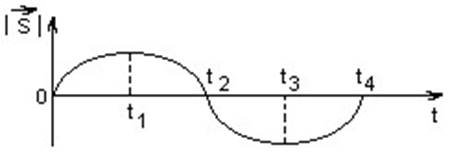
Розв’язання:

Графік залежності проекції швидкості від часу

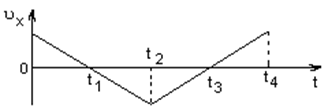
Графік залежності прискорення від часу

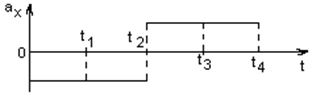
Графік залежності шляху від часу

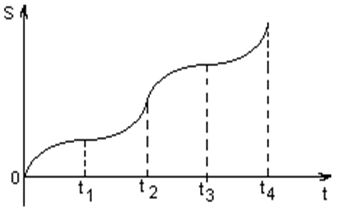
На першій ділянці 0< t<t₂ рух рівносповільнений, 

на другій ділянці t₂< t<t₄  - рух рівноприскорений.

Задача 2.  Кільцевою дорогою рухаються два автомобілі. При русі автомобілів назустріч один одному вони зустрічаються через кожні 8 хв. Якщо автомобілі рухаються кільцем в одному напрямку, то другий автомобіль наздоганяє перший через кожні 56 хвилин за який час проходить кільцеву дорогу кожний автомобіль?

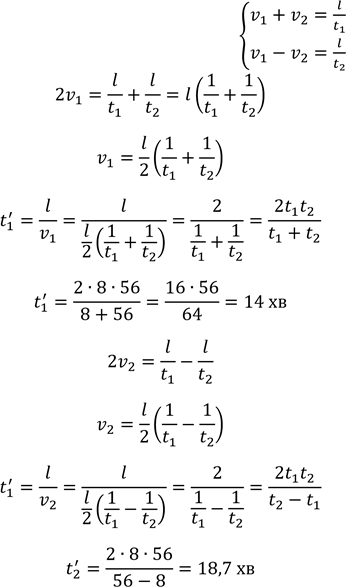
Розв’язання:

1)    𝑣₁𝑡₁ + 𝑣₂𝑡₂ = 𝑙

2)    𝑙₁ − 𝑙₂ = 𝑣₁𝑡₂ − 𝑣₂𝑡₂ = 𝑙

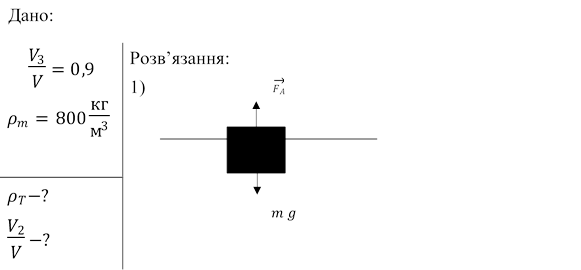
Задача 3. Дерев’яне тіло плаває у воді так, що у воду занурено 90% його об’єму. Яка густина тіла? Яка частина об’єму тіла зануриться у воду, якщо поверх води налити шар масла густиною 0,8 г/см³, який повністю закриває тіло?

2) Налили шар масла

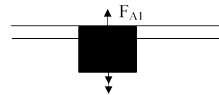
                F_A2 mg

Відповідь:  

Задача 4. До мережі підключені паралельно електричний чайник і каструля, які споживають потужності Р₁=600 Вт та Р₂= 1200 Вт відповідно. Вода в них закипає одночасно через 20хв. На скільки хвилин пізніше закипить вода в каструлі, ніж у чайнику, якщо їх підключити до тієї ж мережі послідовно? 

Дано: СІ:                              Розв’язання:

Р₁=600 Вт                                                     1)Q=P₁t 2) ∆t=t₂-t Р₂=1200 Вт                                                   Q_K = P₂t Q_ч=P₁₁t₁₁     t=20 хв 1200с                            Q_ч                       Q_K=P₂₁t₂₁

𝑈2

∆ t-?                                                             Q_K=

  ;       

;      ;

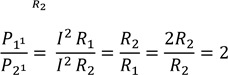
𝑡₂ = 4𝑡₁, тоді     ∆𝑡 = 4𝑡₁ − 𝑡₁ = 3𝑡₁

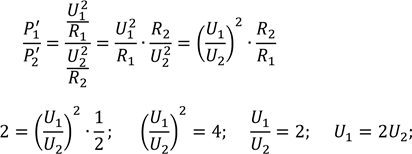
𝑈₁ + 𝑈₂ = 𝑈

2𝑈₂ + 𝑈₂ = 𝑈

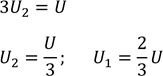
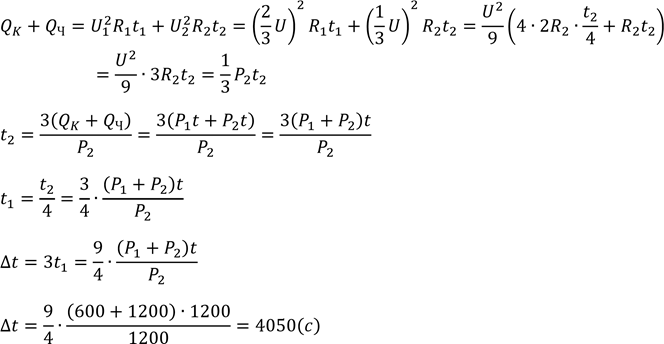
4050𝑐 = 67,5хв

Відповідь: 67,5 хв.

Задача 5. Мініатюрний калориметр масою 0,22 г з питомою теплоємністю

кДж⁄кг ∙ ℃, дає можливість виміряти зміни температури не менші за матеріалу 2,8

0,01 ℃. В калориметр з висоти 5,2 м падає крапля води. За якого мінімального об’єму краплі термометр зможе зафіксувати її попадання в калориметр.

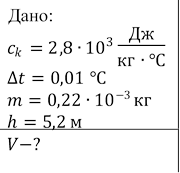Розв’язання:

За законом збереження енергії

∆𝐸_𝑛 = 𝑄 = 𝑄₁ + 𝑄₂

(зміна потенціальної енергії витрачається на нагрівання калориметра та води).

𝑄₁ = 𝑐_𝑘𝑚∆𝑡,          𝑄₂ = 𝑐_в𝑚_к∆𝑡

∆𝐸_𝑛 = 𝑚_к𝑔ℎ

𝑚_к𝑔ℎ = 𝑐_𝑘𝑚∆𝑡 + 𝑐_в𝑚_к∆𝑡

𝑚_к = 𝜌_в𝑉 – маса краплі

𝑚_к𝑔ℎ − 𝑐_в𝑚_к∆𝑡 = 𝑐_𝑘𝑚∆𝑡

𝑚_к(𝑔ℎ − 𝑐_в∆𝑡) = 𝑐_𝑘𝑚∆𝑡

𝜌𝑉(𝑔ℎ − 𝑐_в∆𝑡) = 𝑐_𝑘𝑚∆𝑡

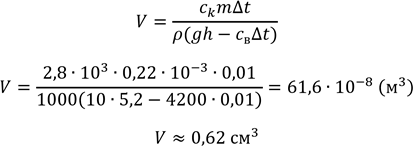
Відповідь:  

Задача 6. Дві однокові невеликі зарядженні металеві кульки () притягуються  з силою 1мН, знаходячись на відстані 3 м одна від одної. Знайдіть заряди кульок . На короткий проміжок часу  кульки з’єднують тонким дротом. Виявилось, що після цього сила взаємодії між кульками зменшилася у 9 разів. Визначте середнє значення сили струму, що пройшов через дріт.

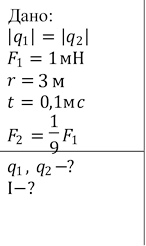
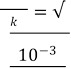
СІ: Розв’язання:

 Нехай, |𝑞₁| = |𝑞₂| = 𝑞

                                                                                  10−3Н  𝑞1𝑞2                           𝑞2

                                                                                 𝐹₁ = 𝑘               𝑟2      = 𝑘 𝑟2

10−4𝑐  ² = 𝐹1𝑟2

                                                                                                 𝑞       

𝑘

                                                                                                  𝑞 = √𝐹₁𝑟2                     𝐹₁ 𝑟 

𝑘

1          ⁻⁶ ∗ 3 = 10⁻⁶ (Кл) 𝑞 = √9 ∗ 10₉ ∗ 3 = 3 ∗ 10

Якщо з’єднати кульки провідником, по ньому піде електричний струм 

заряд, що встигне пройти за даний проміжок часу.

Тоді  нові утворені заряди:

,     

Cила взаємодії  

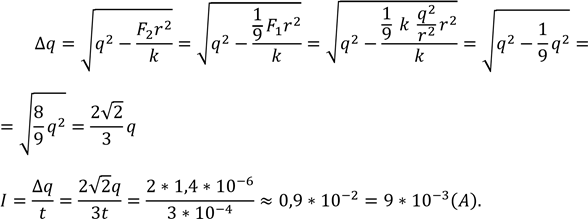
Відповідь: 1мкКл; 9мА.  

Задача 7. Плоский повітряний конденсатор одним краєм доторкнули до поверхні спирту. Яку різницю потенціалів треба прикласти, щоб спирт піднявся на висоту 10 см. Відстань між пластинами 1 мм, діелектрична проникність спирту 25, густина 7100 кг/м³. Капілярністю пластин можна знехтувати.

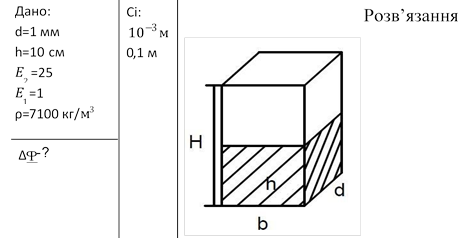
Робота по підняттю спирту дорівнює різниці енергій до і після підняття спирту в конденсатор.

𝐴 = 𝛥𝑊

- з урахуванням центру мас рідини.

ΔႴ = 𝑈 = 6 кВ

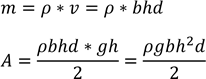
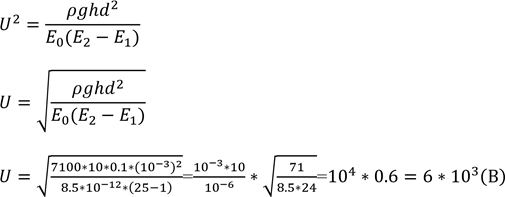
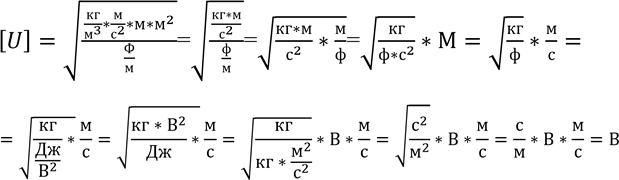
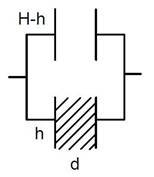
Відповідь: 6 кВ. Задача 8. Схема складається з 100 лампочок опором по 100Ом кожна. Напруга на ділянці 100 В, знайти силу струму на цій ділянці, якщо опір кожної ділянки підвідного горизонтального дроту 1 Ом, а опором вертикальних дротів можна знехтувати.

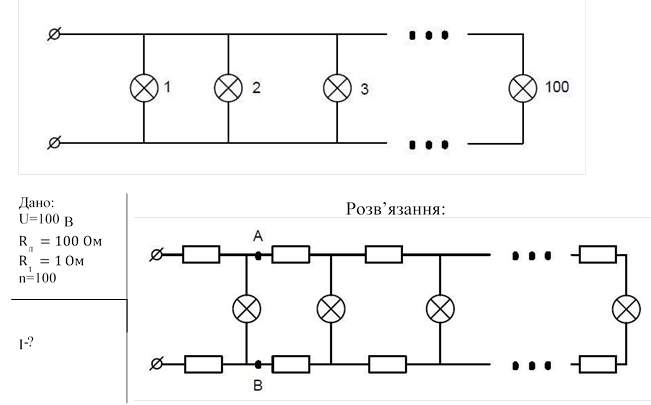
Врахувавши опір горизонтальної ділянки і нехтуючи опором вертикальної, схему можна представити як на малюнку.

Тоді за законом Ома для ділянки кола .

Опір між точками А і В налічує 99 лампочок і майже такий як і всієї схеми.

Тоді    

Розв’яжемо рівняння відносно R:

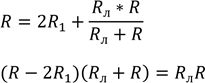
𝑅𝑅_л − 2𝑅₁𝑅_л + 𝑅² − 2𝑅₁𝑅 − 𝑅_л𝑅 = 0

𝑅² + 𝑅_л𝑅 − 𝑅_л𝑅 − 2𝑅₁𝑅 − 2𝑅₁𝑅_л = 0

𝑅² − 2𝑅₁𝑅 − 2𝑅₁𝑅_л = 0

D=4𝑅₁² + 4 ∗ 2𝑅₁𝑅_л = 4𝑅₁(𝑅₁₊2𝑅_л) > 0

 – не задовольняє фізичний зміст задачі.

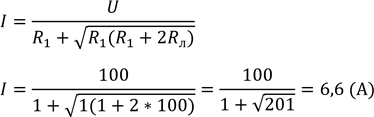
Відповідь: 6,6 А.

Задача 9. Три сферичні краплі ртуті радіусами 3, 4 і 5 мм, заряджені до потенціалу 100 В кожна, зливаються в одну краплю. Визначте її потенціал. Потенціал електричного поля ззовні сферичного заряду на відстані r від його центру визначається за формулою .

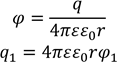                Дано:                          СІ: Розв’язання:

                𝑟₁ = 3 мм               3

                𝑟₂ = 4 мм               ∙ 10⁻³ м

                𝑟₃ = 5 мм               4

                 𝜑_𝑖 = 100 В                             ∙ 10⁻³ м 𝑞₂ = 4𝜋𝜀𝜀₀𝑟𝜑₂

                𝜑−?                                            5𝑞₃ = 4𝜋𝜀𝜀₀𝑟𝜑₃

∙ 10⁻³ м

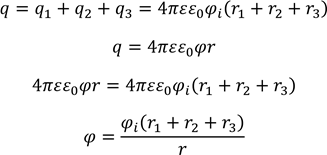
При злитті трьох крапель об’єм нової краплі дорівнює сумі об’ємів крапель:

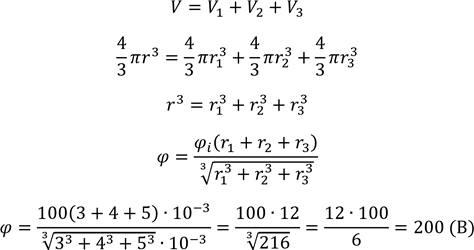
Відповідь: 200 В.

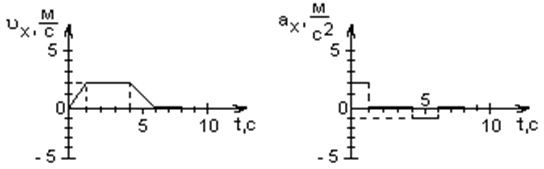
Задача 10. За графіком залежності координати тіла від часу побудувати графік залежності проекції швидкості та прискорення цього тіла від часу.

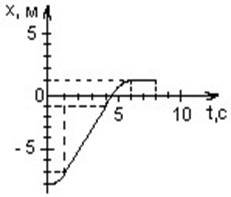
Розв’язання: