«Значення синуса, косинуса й тангенса деяких кутів»
Конспект уроку
на тему:
«Значення синуса, косинуса й тангенса деяких кутів»
Підготувала вчитель-методист Кременецької ЗОШ І-ІІІ ст. №1
ім.Галини Гордасевич Алкіна Галина Володимирівна
Тема. Значення синуса, косинуса й тангенса деяких кутів
Мета:
навчальна:
-
засвоїти спосіб обчислення значень синуса, косинуса та тангенса для кутів
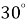 ,
, 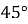 ,
, 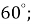
-
навчитися розв’язувати задачі на знаходження синуса, косинуса та тангенса кутів
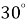 ,
, 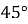 ,
, 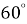 ;
;
-
навчитися розв’язувати задачі з використанням значень синуса, косинуса кутів
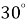 ,
, 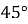 ,
, 
розвивальна:
- розвивати пам’ять;
- розвивати основні процеси мислення;
- сформувати вміння систематизувати дані у таблицю;
виховна:
- виховувати потребу у знаннях;
- виховувати потребу у вміннях;
- виховувати позитивне ставлення до навчання.
Тип уроку: урок засвоєння нових знань, умінь та навичок.
Обладнання та наочність: підручник з геометрії за 8 клас, автор: Істер, Нова програма
Хід уроку
- Організаційний момент.
- Налаштовування на роботу.
- Перевірка домашнього завдання:
(§20 № 712(2-3, 5), 718)
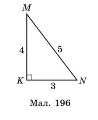 № 712. У
№ 712. У ![]() (мал. 196). Знайдіть:
(мал. 196). Знайдіть:
2) ![]() ; 3)
; 3) ![]() ; 5)
; 5) ![]() .
.
2) ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() ;
;
5) ![]() ,
, ![]() .
.
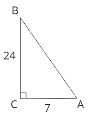 № 718. Дано
№ 718. Дано ![]() ,
, ![]() см,
см, ![]() см. Знайти:
см. Знайти: ![]() ,
, ![]() .
.
![]() ,
, ![]() ,
,![]()
![]() ,
, ![]() ,
, ![]() .
.
- Повідомлення теми і мети уроку.
- Актуалізація опорних знань.
§20 № 719 (співвідношення між сторонами і кутами прямокутного трикутника)
№ 723. У ![]() :
:
1) ![]() , якщо
, якщо ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ;
;
2) ![]() , якщо
, якщо ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() .
.
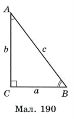
§20 с. 136 Задача 1. У трикутнику ![]() ,
, ![]() см,
см, ![]() .
.
 Знайдіть
Знайдіть ![]() .
.
Розв’язування
Скористаємося малюнком 190. ![]() (см).
(см).
Отже, ![]() (см).
(см).
Відповідь. 16 см.
- Вивчення нового матеріалу
1. Спосіб обчислення синуса, косинуса і тангенса кутів ![]() і
і ![]() .
.
Розглянемо ![]() , у якого
, у якого ![]() ,
, ![]() ,
, ![]() ,
, ![]() (мал. 192). Тоді за властивістю катета, що лежить проти кута
(мал. 192). Тоді за властивістю катета, що лежить проти кута ![]() , AB = 2a.
, AB = 2a.
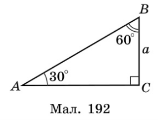
За теоремою Піфагора:
![]()
![]() .
.
Тоді
![]() , тобто
, тобто ![]() ;
;
![]() , тобто
, тобто ![]() ;
;
![]() , тобто
, тобто ![]() ;
;
![]() , тобто
, тобто ![]() ;
;
![]() , тобто
, тобто ![]() ;
;
![]() , тобто
, тобто ![]() .
.
2. Спосіб обчислення синуса, косинуса і тангенса кутів ![]() .
.
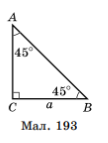 Розглянемо
Розглянемо ![]() , у якого
, у якого ![]() ,
, ![]() ,
,
![]() (мал. 193). Тоді AC = BC = a.
(мал. 193). Тоді AC = BC = a.
За теоремою Піфагора: ![]()
![]() .
.
Тоді
![]() , тобто
, тобто ![]() ;
;
![]() , тобто
, тобто ![]() ;
;
![]() , тобто
, тобто ![]() .
.
- Систематизація отриманих даних у таблицю.
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- Закріплення нового матеріалу
(§20 № 715, 723, §21 756(1, 2), 758(1, 4))
№ 715. Обчисліть:
1) ![]() ;
;
2) ![]()
1) ![]() ;
;
2) ![]() .
.
№ 723. У ![]() :
:
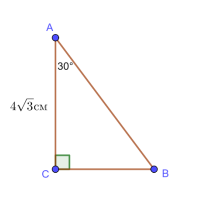 1)
1) ![]() , якщо
, якщо ![]() cм,
cм, ![]()
Дано: ![]()
![]() ,
,![]() см.
см.
Знайти: ![]() .
.
Розв’язання
![]() .
.
![]() (см).
(см).
![]() см.
см.
Відповідь: 8 см.
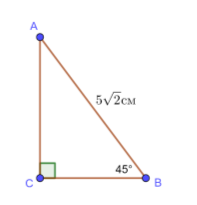 2)
2) ![]() , якщо
, якщо ![]() cм,
cм, ![]()
Дано: ![]() ,
,
![]() ,
,![]() см.
см.
Знайти: ![]() .
.
Розв’язання
![]() .
.
![]() (см).
(см).
![]() см.
см.
Відповідь: 5 см.
№ 756. За гіпотенузою ![]() прямокутного трикутника
прямокутного трикутника ![]() і гострим кутом знайдіть інші його сторони та другий гострий кут .
і гострим кутом знайдіть інші його сторони та другий гострий кут .
1) ![]() cм,
cм, ![]()
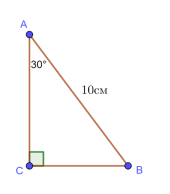 Дано:
Дано: ![]() ,
,
![]() ,
, ![]() ,
,![]() см.
см.
Знайти: ![]() .
.
Розв’язання
За теоремою про суму кутів трикутника
![]()
![]() ,
, ![]() .
.
За умовою ![]() см, тоді
см, тоді
![]() =
= ![]() (см),
(см),
![]() (см).
(см).
Відповідь: ![]() см,
см, ![]() см,
см, ![]() .
.
2) ![]() дм,
дм, ![]()
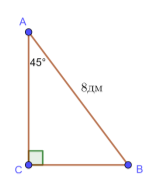 Дано:
Дано: ![]() ,
,
![]() ,
, ![]() ,
,![]() дм.
дм.
Знайти: ![]() .
.
Розв’язання
За теоремою про суму кутів трикутника
![]()
![]() ,
, ![]() .
.
За умовою ![]() дм, тоді
дм, тоді
![]() =
= ![]() (дм).
(дм).
Відповідь: ![]() дм,
дм, ![]() дм,
дм, ![]() .
.
№ 758. За катетом трикутника ![]() і гострим кутом знайдіть інші сторони та другий гострий кут трикутника.
і гострим кутом знайдіть інші сторони та другий гострий кут трикутника.
1) ![]() см,
см, ![]()
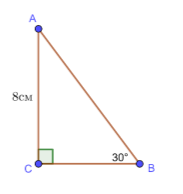 Дано:
Дано: ![]()
![]() ,
, ![]() ,
,![]() cм.
cм.
Знайти: ![]() .
.
Розв’язання
За теоремою про суму кутів трикутника
![]()
![]() , за умовою
, за умовою ![]() см, тоді
см, тоді
![]() (см).
(см).
![]() ,
, ![]() (см).
(см).
Відповідь: ![]() cм,
cм, ![]() cм,
cм, ![]() .
.
4) ![]() см,
см, ![]()
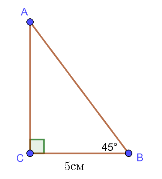 Дано:
Дано: ![]()
![]() ,
, ![]() ,
,![]() cм.
cм.
Знайти: ![]() .
.
Розв’язання
За теоремою про суму кутів трикутника
![]()
![]() (см).
(см).
![]() (см),
(см), ![]() , (см).
, (см).
Відповідь: ![]() cм,
cм, ![]() cм,
cм, ![]() .
.
- Висновки
На уроці ми пригадали методи розв’язування прямокутних трикутників, рівнобедрених трикутників та теорему Піфагора; розглянули спосіб обчислення значень синуса, косинуса та тангенса для кутів ![]() ,
, ![]() ,
, ![]() навчилися розв’язувати задачі на знаходження синуса, косинуса та тангенса кутів
навчилися розв’язувати задачі на знаходження синуса, косинуса та тангенса кутів ![]() ,
, ![]() ,
, ![]() та задачі на використання цих значень.
та задачі на використання цих значень.
- Домашнє завдання
(§20 № 716, 724, §21 757(1, 2), 759(1, 4))


про публікацію авторської розробки
Додати розробку
