Конспект уроку з геометрії на тему "Площа круга та його частин"

Урок  геометрії

 

Тема уроку: Площа круга та його частин.

Мета уроку: виведення формули для знаходження площі круга, кругового сектора, кругового сегмента. Формування вмінь учнів застосовувати виведені формули до розв’язування задач.розвивати логічне мислення та графічну культуру.Показати практичне застосування формул. 

 

Хід уроку

І.Організаційний момент.

ІІ.Актуалізація опорних знань.

1)Яка геометрична фігура називається кругом?

2)Які елементи круга ви можете назвати?

3) Який кут називається центральним?

4) Які одиниці вимірювання площі ви знаєте?

. 

ІІІ.Пояснення нового матеріалу.

  Кругом називається частина площини, обмежена колом. Кругом радіуса R з центром у точці О називається точка О і всі точки площини, які містяться від точки О на відстані, не більшій від R.

Круг обмежений колом. Його не можна розбити на многокут­ники і обчислити площу як суму многокутників. Дамо означення площі круга таким чином.

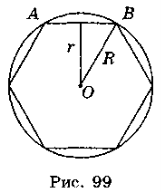Площею круга називається величина, до якої наближається площа вписаного в це коло правильного многокутника за умови, що число його сторін необмежено збільшується.

Впишемо в коло радіусом R правильний п-кутник. Площа правильного многокутника

S_n = nS_ΔAOB = n ∙ r ∙ АВ = Р_пr, де Р_n — пери­метр правильного п-кутника.

При необмеженому збільшенні п площа правильного многокутника S_n наближається до площі круга, Р_п — до довжини кола, r — до R. Отже, одержуємо:

S_кр = CR= ∙ 2πR ∙ R = πR².

Таким чином, площу круга можна обчислити за формулою S_кр = πR².

Формула дозволяє знаходити площу круга за його радіусом, а також знаходити радіус круга за відомою площею круга.

 

Знаходження площі кругового сектора

Користуючись формулою площі круга, можна вивести фор­мули для знаходження площі частин круга, зокрема кругового сектора і кругового сегмента.

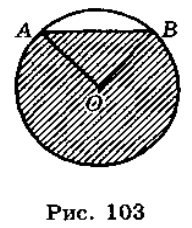
Круговим сектором називається частина круга, яка лежить усередині центрального кута .

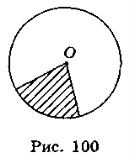
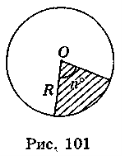
Спираючись на формулу площі круга, виведемо формулу для площі сектора, кутова величина дуги якого дорівнює α° .

, якщо відповідний центральний кут має радіанну міру α = k, то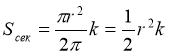

 

Сегментом називається частина круга, обмежена хордою і відповідною дугою. Відповідну дугу називають основою сегмента, а відрізок діаметра перпендикулярного до неї і розміщеного всередині сегмента називають висотою сегмента.                                         

 

 

 

 

 

 

 

 

 

 

 

 

 

                                            

 

 

 

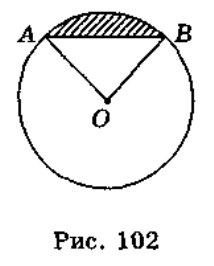
IV.Розв’язування задач і вправ.

 

Розв’язування усних вправ.

1) Знайдіть площу круга радіуса  3см;10см.(9π см²; 100πсм²)

2) Знайдіть площу круга , діаметр якого дорівнює18см.( 81πсм²)

3) Знайдіть радіус круга, якщо його площа становить16πсм².(4см)

4) Завдання 14 з підручника:

      Впр.3.Як зміниться площа круга, якщо його радіус :а)збільшиться вдвічі; б)зменшиться в 5 разів?(збільшиться в 4рази; зменшиться в 25разів)

      Впр.4.Як зміниться площа круга, якщо діаметр круга збільшити вдвічі?(збільшиться в 4 рази)

 

 

 5) Чи може площа правильного многокутника, вписаного в коло, бути більшою за площу круга, обмеженого даним колом?(ні)

6) Чому ,на вашу думку, каналізаційні люки  круглі, а не квадратні?(порівняти сторону квадрата з його діагоналлю)

7 ) Коло має ще одну цікаву властивість. Візьмем мотузку и зв’яжем її в кільце. Покладемо отримане кільце на площину і зробимо з нього різні фігури: квадрат, трикутник, коло та ін. Площа, обмежена колом ( площа круга) – найбільша серед отриманих таким чином площ.

 

 

Математична естафета.

1. Знайдіть площу круга радіуса 10 см. (Відповідь. 100π см².)
2. Знайдіть радіус круга, площа якого дорівнює 25π см². (Відпо­відь. 5 см.)
3. Знайдіть площу, обмежену колом ,довжина якого становить 20πсм.
4. Знайдіть площу сектора круга,радіус якого дорівнює 6см, а центральний кут 40˚.
5. Знайдіть площу сектора круга, діаметр якого дорівнює 10см, а відповідний центральний кут дорівнює .

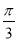Виконання графічних вправ.

 

• Намалюйте коло;
• Впишіть в це коло правильний трикутник;
• Заштрихуйте утворені сегменти;

            Знайдіть площу заштрихованих фігур.

 

          Розв’язування задач.

1) (ЗНО 2011) У прямокутник АВСD, вписано три круги одного й того самого радіуса. Визначити довжину сторони ВС, якщо загальна площа кругів дорівнює 3π.

Відповідь :6

2) Знайдіть площу круга довжина кола, якого дорівнює 6π см. (9πсм²)

 

3) Вправа 17ст.106.

Довжина кола циркової арени дорівнює 42м. Знайдіть діаметр і площу арени.

(R=8м,S=147)

 

4)Радіус дії антени вишки мобільного зв’язку 30км. Знайдіть площу мобільного покриття;

На якій відстані, на вашу думку, необхідно встановлювати інші вишки, для уникнення “мертвих зон”. (900πкм^{2  ,}20-25км)

 

5)Знайдіть площу круга, описаного навколо квадрата, площа якого дорівнює 8см²

 

 

6) Знайдіть площу кругового кільця, обмеженого двома концентричними колами, радіуси яких дорівнюють 4см і 6см. (20πсм²)

 

 7)Площа сектора становить    площі круга. Знайдіть градусну міру центрального          кута, який відповідає даному сектору.

 

   8)Знайдіть радіус круга, якщо площа сектора цього круга 45см² , а центральний кут, що відповідає цьому сектору, дорівнює 72˚.

 

9 )Площа кругового сектора з центральним кутом 45° дорівнює 8πсм². Знайдіть радіус сектора.

 

10) Знайдіть кутову величину дуги кругового сектора, якщо радіус кола становить 4 см, а площа сектора дорівнює 4π см².

 

11) Площа одного круга в 16 разів більша за площу іншого круга. Знайдіть відношення радіусів цих кіл.

12) (ЗНО 2010)

Два кола дотикаються, причому менше з кіл проходить через центр більшого кола. Знайдіть площу зафарбованої фігури, якщо менше з кіл обмежує круг площею 64см.

 (Площі фігур відносяться як квадрати відповідних елементів.)

 

13) Знайдіть площу кругового кільця, що міститься між описаним і вписаним колами правильного шестикутника зі стороною 6 см.

 

 14)Клумбу, діаметром 8м потрібно розбити на 8 рівних секторів для квітів різних видів.      Скільки квітів одного виду можна посадити, якщо для кожної квітки необхідно.

 

15)У півкруг, діаметр якого 16см, вписано прямокутний трикутник, гіпотенуза якого збігається з діаметром півкруга, а один з кутів дорівнює 30˚. Визначте площу тієї частини півкруга, яка лежить поза трикутником.

 

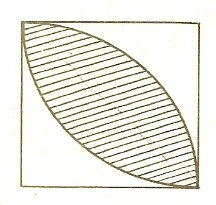
 16)Знайдіть площу заштрихованої фігури,якщо квадрат має сторону і дуги кіл  радіуса 1.

 

 

 

 

 

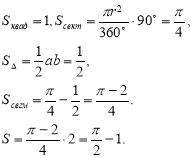
Домашнє завдвння:§17,Завд.817,820

 

Підсумок урок.

 

 

Використана літратура

1. Геометрія 9 клас
2. Завдання ЗНО минулих років
3. schoollife.org.ua
4. metodportal.net/node/54945