№1

 

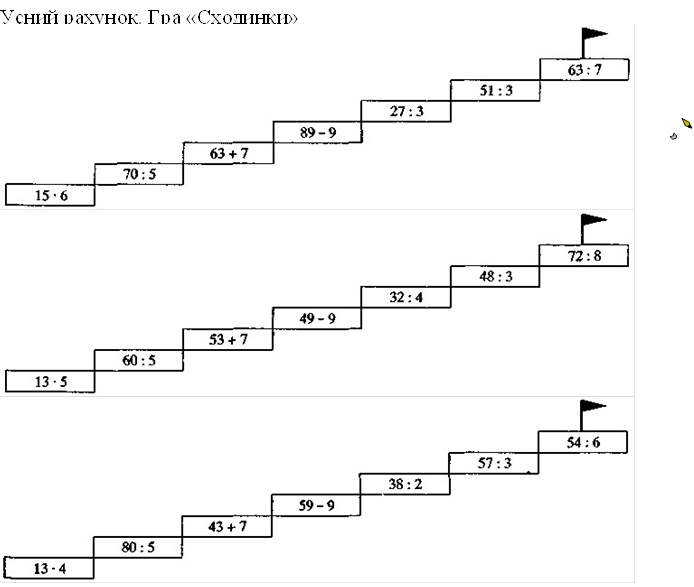
№2

Замініть додавання множенням:

                а) 7 + 7 + 7;          б) 4 + 4 + 4 + 4 + 4;       в) 3 + 3 + 3 + 3.

 

№3

Замініть множення додаванням:

                а) 5 · 3;                б) 9 · 4;                         в) 8 · 5.

 

№4 Виконайте множення:

           а) 46 · 12;        б) 354 · 12;            в) 1473 · 2;            г) 2636 · 21. №5

Виконайте дії двома способами. Зробіть висновки.

           а) (807 – 527) · 63;                 б) (89 + 77) · 47.

 

№6

Пульс здорової людини становить близько 75 ударів за хвилину. Скільки буде ударів пульсу за годину; за добу; за рік?

 

№7

Пташенята під час свого росту дуже ненажерливі. Стриж ловить дрібних комах на льоту і годує своїх пташенят порівняно з іншими птахами рідко, лише 20 разів на день, зате приносить щоразу в середньому по 370 дрібних комах. Скільки комах наловить пара стрижів за 32 дні (період вигодовування пташенят)?

 

№8

Виконайте ділення. (Учні виконують ділення з повним коментуванням.)              а) 782 : 23; б) 1134 : 42;          в) 77000 : 25;        г) 8610 : 246.

 

№9

Знайдіть х. 

              а) 18х = 90;                б) 380 : х = 20;     в) х : 37 = 28.

 

№10

Визначаючи кількість води, яку дає джерело, туристи помітили, що дволітрова банка наповнилася за 4 секунди. Скільки води дає джерело за годину? за добу? №11

«Склади слово»

0	1	2	3	4	5	6	7	8	9
І	Ш	К	П	А	У	Л	Н	Т	0

1) 747956 – 506109                                     3) 782758 – 626734 2) 239473 + 126424                                     4) 11238 + 19226.

 

№12

«Де живе осінь?»

Щоб дати відповідь на це запитання, треба знайти значення виразу, що записаний на дошці, і поставити у відповідність результатам дій букву у таблиці.

1000 – (119 + 283) + (544 – 457) – 137∙5 = 0  1) 119 +238 =                         2) 544 – 457 =  3) 137∙5 =                                4) 1000 – 402 = 

5) 598 + 87 =                            6) 685 – 685 = 

87	0	402	598	685
л	!	у	с	і

 

№13 «Забий гол!»

Пограймо в математичний футбол! Зафарбуй кружечки з числом-відповіддю, щоб «забити» гол.

 

 

 

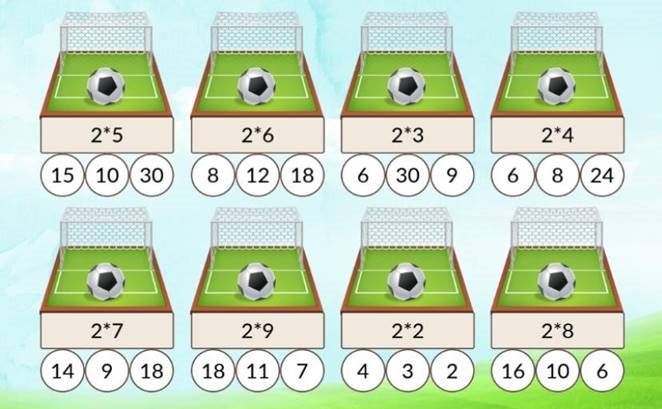
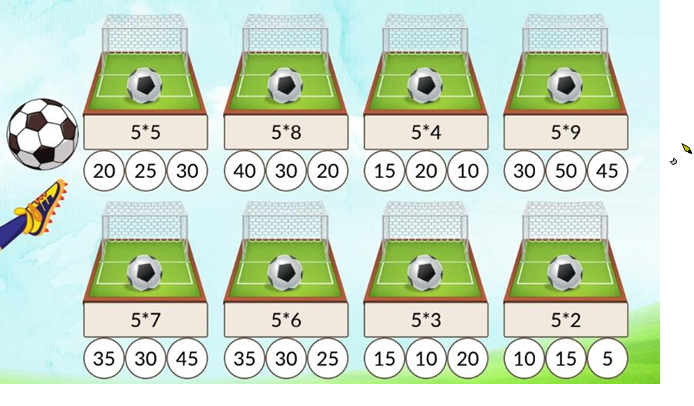
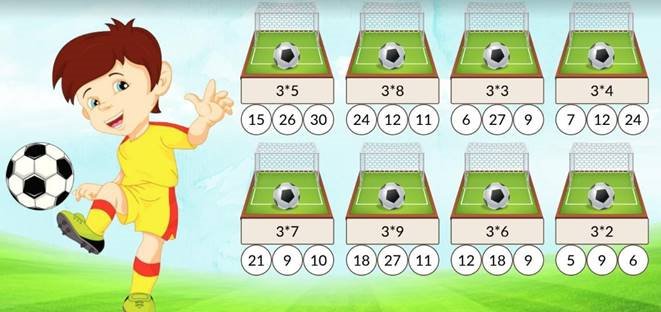
№14

У ящики по 10 кг і 5кг розклали 600кг огірків, п’ятикілограмових ящиків було 26. Скільки знадобилось ящиків місткістю по 10 кг? 

 

№15

Автомобіль  проїхав  240 км за3 год. Швидкість мотоцикліста на 5 км/год менша від швидкості автомобіля. Скільки кілометрів проїде мотоцикліст а 2 години?  

 

 

 

№16

За продаж моркви й буряків сім’я фермерів отримала 7800 грн. за моркву отримала 1/3 всієї виручки, решту за буряки. На скільки більше отримали за буряки, ніж за моркву?

 

№17

Збираючись у гості до своєї бабусі, Карлсон вирішив підкріпитися. На сніданок він з’їв 26 банок варення, а на обід – на 16 банок більше. Скільки банок варення з’їв Карлсон?

 

№18

На одній ділянці ростуть 34 кущі смородини, а на другій – на 18 кущів менше. Скільки всього кущів смородини росте на обох ділянках?

 

№19

Обчисліть 7 кг 750 г  24.

 

№20

Яке число є розв’язком рівняння  х – 2856 = 4456?

 

№21

Учень прочитав 40 сторінок, що становить    усієї книжки . Скільки всього сторінок у книжці?

 

№22

Порівняйте   год   і  25 хв.

 

№23

Розв’яжіть рівняння  (х + 2508) – 6709 = 2407.

 

№24

За три дні магазин продав 1 т 380 кг овочів. За перший день продав  усіх овочів, а за другий –  того, що було продано за перший день. Скільки кілограмів овочів продав магазин за третій день?

 

№25

Який із прямокутників має  найбільшу площу?

                А) 4 см і 7 см;      Б) 9 см і 3 см;       В) 6 см і 3 см.

 

№26

Порівняйте  2 т 8 ц  і  2 т 800 кг.

 

 

 

 

№27

Із двох  міст,  відстань між якими 28 км, одночасно назустріч один одному виїхали два велосипедисти. Яка відстань буде між ними, коли  перший проїде  , 

а другий –  всієї відстані?

 

№28

Обчисліть  452440 : 4 – (9150 + 890).

 

№29

Із двох міст одночасно назустріч один одному  виїхали мотоцикліст зі швидкістю 70 км/год і велосипедист,  швидкість  якого у 5 разів менша. Вони зустрілись через 3 год. Знайдіть відстань між містами.

 

№30

Периметр квадрата дорівнює 24 см. Яка довжина його сторони?

13. Сад має форму прямокутника, ширина якого 70 м, а довжина – втричі більша.

 площі саду засаджена яблунями, а решта – сливами. Яка площа саду засаджена

сливами?

 

№31

Яке число є розв’язком рівняння  х : (71000 −53252) = 3?

 

№32

Велосипедист і мотоцикліст одночасно вирушили у протилежних напрямках. Велосипедист рухався зі швидкістю 15 км/год, а мотоцикліст − зі швидкістю у 3 рази більшою. Через який  час відстань між ними становитимете 120 км?

 

№33

Розв’яжіть рівняння  (2240 + х)  5 = 64600.

 

№34

Обчисліть  (1000 – 36202 : 46)  82.

 

№35

Порівняйте  10 км 52 м  і  1045 м.

 

№36

Частку чисел 784 і 28  збільшить у 14 разів.

 

№37

Знайдіть значення виразу  513 : (75 – 324 : 18) + 72.

Натуральні числа — це числа, що використовуються для

лічби: 1,2,3,.... n.... Множину натуральних чисел позначають символом N. N={1,

2, 3,...}

Будь-яке натуральне число п у десятковій системі числення можна подати у вигляді:

^k                         k-1∙ 10^k-1 + ... + а₂ ∙10² + а₁ ∙ 10¹ + а₀,

                                                                                0      _{1       2                k-1}можуть набувати значення 0,1, 2, 3,

4, 5, 6, 7, 8, 9, а число аk — значення 1, 2, 3, 4, 5, 6, 7, 8, 9.

Приклади:

 581 = 5 ∙ 10² + 8 ∙ 10 + 1; 

25 847 = 2 ∙ 10⁴ + 5 ∙ 10³ + 8 ∙ 10² + 4 ∙ 10 + 7.

 

Порівняння натуральних чисел.

Порівняти два натуральних числа – означає з’ясувати, яке з них більше, а яке – менше. Результати порівняння записують за допомогою знаків менше (<) або більше (>). Такі записи називаються нерівностями.

Із двох натуральних чисел, які розміщені на координатному промені, більше те, яке розміщене правіше, і менше те, що розміщене лівіше.

Якщо натуральні числа мають різну кількість цифр, то більше те число, в запису якого більше цифр, і менше те число, в запису якого менше цифр.

Якщо в запису натуральних чисел однакова кількість цифр, то для їх порівняння користуються таким правилом:

Із двох натуральних чисел з однаковою кількістю цифр більшим є те, у якого більшою є перша з неоднакових цифр. При цьому порівняння здійснюють, рухаючись зліва направо.

 

Приклади: 117568 > 1907; 24267 < 24367.

 

 

 

Округлення натуральних чисел.

1)   округлюючи натуральне число до певного розряду, всі цифри, що йдуть за ним, замінюють нулями;

2)   якщо перша наступна за цим розрядом цифра 5,

6, 7, 8 або 9, то останню цифру, яка залишилася, збільшують      на      одиницю;    якщо перша наступна за цим розрядом цифра 0, 1, 2, 3 або 4, то останню цифру, яка залишилася, не змінюють.

Приклад 1. Округлити число 85 357 до тисяч.

Приклад 2. Округлити  число 68 792 до найвищого

Найвищим розрядом даного числа є десятки тисяч. Тому цифри 8, 7, 9 та 2 замінюємо нулями. Цифру в розряді десятків тисяч 6 збільшуємо на одиницю, оскільки наступна за нею цифра 8. 

Отже: 68 972 ≈ 70 000.

 

Дії над натуральними числами.

Додавання.

У записі 𝑎 + 𝑏 = 𝑐 числа a і b — доданки, число с, а також вираз 𝑎 + 𝑏— сума чисел а і b.

 

Додавання багатоцифрових натуральних чисел виконується порозрядно (додавання одноцифрових чисел кожного стовпчика, починаючи з правого стовпчика).

 

 

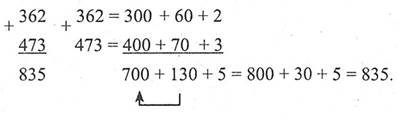
Властивості додавання:

1.   Переставна. Від перестановки доданків сума не змінюється: 𝑎 + 𝑏 = 𝑏 + 𝑐.

2.   Сполучна. Щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого й третього чисел: (𝑎 + 𝑏) + 𝑐 = 𝑎 + (𝑏 + 𝑐). Переставна й сполучна властивості додавання дають змогу виконувати додавання кількох чисел у будь-якій послідовності.

3.   Якщо один із двох доданків 0, то їх сума дорівнює другому доданку:

𝑎 + 0 = 𝑎, 0 + 𝑎 = 𝑎

Віднімання.

Дія, за допомогою якої за відомою сумою двох доданків і одним із них знаходять другий доданок, називається дією віднімання: 𝑎 − 𝑏 = 𝑐.У цьому записі число а — зменшуване, b — від’ємник, c — різниця. Різниця двох натуральних чисел показує, на скільки перше число більше від другого або на скільки друге число менше від першого.

Віднімання багатоцифрових натуральних чисел виконується порозрядно (віднімання одноцифрових чисел кожного стовпчика, починаючи з правого стовпчика).

 

 

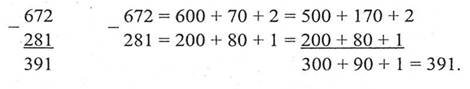
Властивості віднімання.

1.   Щоб відняти суму від числа, можна спочатку відняти від цього числа один доданок, а потім від отриманої різниці — другий:

25-(15+3)=(25-15)-3=10-3=7.

2.   Щоб від суми відняти число, можна відняти його від одного з доданків, а до отриманої різниці додати другий доданок:

(37+15)-17=(37-17)+15=20+15=35; (23+19)-9=23+(19-9)=23+10=33.

3.   Якщо від числа відняти нуль, воно не зміниться: 𝑎 − 0 = 𝑎.

4.   Якщо від числа відняти те ж саме число, одержимо 0: 𝑎 − 𝑎 = 0.

 

Множення.

Помножити число a на число b означає знайти суму b доданків, кожний із яких дорівнює а:

𝑎 + 𝑎 + 𝑎 + ⋯ + 𝑎 = 𝑐,  або a∙b=c              b де a і b — множники, c — добуток.

 

Властивості множення.

1.     Переставна. Від перестановки множників добуток не змінюється:   

 𝑎 ∙ 𝑏 = 𝑏 ∙ 𝑎.

2.     Сполучна. Щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого й третього чисел:

   (𝑎 ∙ 𝑏) · 𝑐 = 𝑎 · (𝑏 · 𝑐) = 𝑎 · 𝑏 · 𝑐 .

Множення багатоцифрових натуральних чиселвиконується «у стовпчик».

Наприклад: 459ˑ275=126225.

 

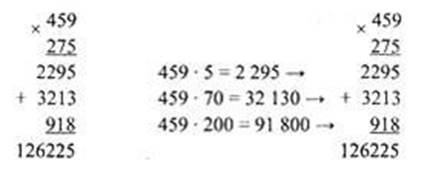
3.     Розподільна.

- Щоб помножити суму на число, можна кожний доданок помножити на це число і знайдені добутки додати:

(𝑎 + 𝑏) ∙ 𝑐 = 𝑎𝑐 + 𝑏𝑐.

-Щоб помножити різницю на число, можна зменшуване і від’ємник помножити на це число й від першого добутку відняти другий:

(𝑎 − 𝑏) ∙ 𝑐 = 𝑎𝑐 − 𝑏𝑐.

4.   Якщо одиницю помножити на будь-яке число, дістанемо те саме число:

𝑎 ∙ 1 = 1 ∙ 𝑎 = 𝑎.

5.   Якщо хоча б один множник дорівнює 0, добуток дорівнює 0:

0 ∙ 𝑎 = 𝑎 ∙ 0 = 0.

Приклади:

68∙7+32∙7=(68+32)∙7=100∙7=700;

59∙5=(60-1) ∙5=60∙5-1∙5=300-5=295.

 

Ділення.

Ділення — дія, за допомогою якої за відомим добутком і одним із множників знаходять другий множник.

Якщо 𝑎 ∙ 𝑏 = 𝑐, то 𝑐: 𝑏 = 𝑎  і 𝑐: 𝑎 = 𝑏 .

У записі 𝑐: 𝑏 = 𝑎  число с — ділене, b — дільник, число а, а також вираз 𝑐: 𝑏— частка.

Частка показує, у скільки разів ділене більше дільника.

 

Ділення багатоцифрових чисел виконується «кутом».

Наприклад:

113 сотень: 28 = 4 сотні (остача 1 сотня);

19 десятків: 28 = 0 десятків (остача 19 десятків); 196 : 28 = 7.

 

 

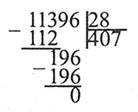
Властивості ділення.

1.   На 0 ділити не можна.

2.   Якщо розділити число на 1, дістанемо те саме число: 𝑎 ∶ 1 = 𝑎.

3.   Якщо розділити число на себе, дістанемо 1: 𝑎: 𝑎 = 1, (𝑎 ≠ 0)   .

4.   Якщо розділити 0 на будь-яке число, крім 0, дістанемо 0: 0 ∶ 𝑎 = 0, (𝑎 ≠ 0).

 

Ділення з остачею.

Число а ділиться на число b націло, якщо  𝑎 = 𝑏 ∙ 𝑛 , де n — яке-небудь натуральне число.

Наприклад, 15 ділиться націло на 3, оскільки 15=3∙5.

В іншому випадку можна поділити а на b з остачею. Наприклад:

.   

289=15∙19+4

У цьому записі число 289 — ділене, 15 — дільник, 19 — неповна частка, 4 — остача. Для будь-яких чисел а та b завжди знайдуться такі числа с і r (натуральні або 0), що a=b∙c+r, де r<b. Коли r=0, то a=b∙c, тобто число а ділиться на число b і на число c.

 

Задачі до теми 2

 

№39

Округліть число 12 475 836:    а) до десятків;

   б) до тисяч;

   в) мільйонів.

№40

Дано три числа: 359; 4 327; 804. Обчислити: суму цих чисел і округлити результат до сотень.

№41

Обчисліть на скільки число 59 428:    а) більше від 54 609;

   б) менше від 79 529.

№42

Обчисліть зручним способом:    а) 274 + 1 537 + 463;

   б) 756 – (356 + 235).

№43

До будівельного майданчику привезли 340 т щебеню, що на 81 т більше, ніж піску, і на 103 т менше, ніж цементу. Скільки всього привезли будівельних матеріалів? №44

Не використовуючи калькулятора, обчисліть, обираючи зручний порядок дій:    а) (1 873 + 1 227) – 873;     б) 641 – (141 – 98);

   в) (797 + 512) – 112;           г) 5 124 + 676 + 4 876.

№45

На залізничну станцію прийшов поїзд із 97 товарних вагонів. Після того, як частину вагонів відчепили, залишилося 48 вагонів. Скільки вагонів відчепили? №46

Знайдіть значення виразу 7 420 : х + 29, якщо х = 7. 

№47

Порівняйте числа, результат порівняння запишіть за допомогою знака «< » або « >

»:

а) 3 000 080  і  3 000 100;      б) 75 102  і  75 201.

№48

Обчисліть, обираючи зручний порядок дій:                                             

а) 4 ·256 ·25;                                          б) 4 ·680 · 25; в) 8 ·100 · 5.  №49

Знайдіть значення виразу: 239 · 37 – 208 · 37 + 169 · 37.

№50

На рисунках, поданих нижче, наведені деякі основні геометричні фігури; поруч даються назви й позначення.

Відрізок AB (або BA).  

Промінь AB.  

Промінь BA.  

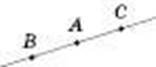
Пряма AB (або a).  

Ламана ABСDЕ.

 

 

 

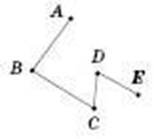
Промені AB і АС — доповняльні.

 

 

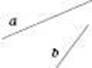
Прямі а і b перетинаються.

 

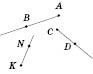
Промені АB і KN перетинаються, AB і CD не перетинаються.

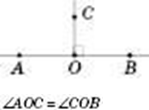
Кут AOB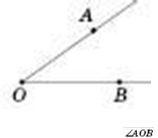. Записують  (або          ,         ). О — вершина кута. Промені OA і OB — сторони кута.

Величини кутів вимірюють за допомогою транспортира.

 — розгорнутий.  

Кут, що дорівнює половині розгорнутого, називається прямим.

 

 — прямі кути.

Один градус — це кут, який становить  частини прямого кута. Отже, прямий кут становить , розгорнутий — .

Якщо величина кута менша від , такий кут називається гострим.

                Кут, величина якого більша за    , але менша від , називається тупим.

 

Гострий кут         Прямий кут       Тупий кут

 

 

Графічний диктант (так , ні __) Визначте, чи є правильним твердження.

1.              Кут, менший за розгорнутий,— тупий.

2.              Будь-який гострий кут менший за половину розгорнутого кута.

3.              Кут, більший від прямого,— тупий.

4.              Кут, менший за прямий,— гострий.

5.              Сума гострого і прямого кутів — тупий кут. 6. Половина тупого кута — гострий кут.

                                                                                                                  Ключ-відповідь

№ 51

Із вершини прямого кута AOC проведено променя OC і OD так, що QCOB₌78_, а QAOD ₌56_. Обчисліть градусну міру кута COD.

№ 52 Накресліть кут ABC, градусна міра якого становить 148°. Променем BD поділіть цей кут на два кути так, щоб QABD ₌96_. Обчисліть градусну міру кута DBC.

№ 53 Накресліть кут, градусна міра якого становить:  а) 36°; б) 90°; в) 153°; г) 98°. 

Позначте кожен з кутів і визначте його вид.

 

Самостійна робота

Варіант 1

Початковий і середній рівні  

Позначте правильну, на вашу думку, відповідь.

1.  Яке позначення кута, зображеного на рис. 5, неправильне?

 

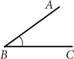
Рис. 5

            А  ےABC                      Б _ےCBA        В _ےB              Г _ےCAB

2.  Градусна міра прямого кута дорівнює:

            А180°                           Б 90°               В 45°              Г 30°

3.  Визначте вид кута, градусна міра якого дорівнює 87°.

            АРозгорнутий             Б Тупий         В Прямий       Г Гострий

Достатній рівень 

4.  Побудуйте кут ABC, градусна міра якого дорівнює 150°, і його бісектрису BK.

5.  Кут PKS удвічі більший, ніж кут SKQ. Знайдіть їх градусні міри, якщо QPKQ=150. Високий рівень 

6.  Із вершини тупого кута ABC проведено промінь BK так, що градусна міра кута АВК більша, ніж кута KBC, на 38°. Знайдіть величини кутів ABK і KBC, якщо бісектриса кута ABC ділить його на кути, один із яких становить 74°.

 

Варіант 2

Початковий і середній рівні 

Позначте правильну, на вашу думку, відповідь.

1. Яке позначення кута, зображеного на рис. 6, неправильне?

 

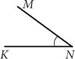
Рис. 6
А ےMNK                      Б ےKNM                   В         ےN 2. Градусна міра розгорнутого кута дорівнює:	Г ےKMN
А 90°                             Б 180°                        В 60°	Г 45°

3.  Визначте вид кута, градусна міра якого становить 123°.

            АТупий                        Б Розгорнутий          В Прямий       Г Гострий

Достатній рівень 

4.  Побудуйте кут MKL, градусна міра якого дорівнює 80°, і його бісектрису KN.

5.  Кут BOK удвічі менший, ніж кут AOB. Знайдіть їх градусні міри, якщо QAOK ₌120_. Високий рівень 

6.  Із вершини гострого кута MNK проведено промінь NL так, що градусна міра кута LNK більша, ніж кута MNL, на 28°. Знайдіть величини кутів MNL і LNK, якщо бісектриса кута MNL ділить його на кути, один із яких становить 38°.

 

 

Многокутник

 

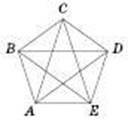
На рисунку ABCDE — п’ятикутник. A, B, С, D, E — вершини п’ятикутника; AB, BC, CD, DE, EA — сторони;

AC, AD, BE, BD, CE — діагоналі.

Окремі види многокутників На рисунках зображені окремі види многокутників. Прямокутник:

b

               a

 𝑃 = 2(𝑎 + 𝑏)— формула периметра.

𝑆 = 𝑎𝑏 — формула площі.

 

Квадрат

 

𝑃 = 4𝑎   — формула периметра.

𝑆 = 𝑎²   — формула площі.

Трикутник

На рисунку зображений трикутник зі сторонами a, b і c.

 

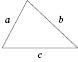
𝑃 = 𝑎 + 𝑏 + 𝑐 — формула периметра трикутника.

Сума всіх кутів довільного трикутника дорівнює . Кожний трикутник має принаймні два гострих кути.

Види трикутників

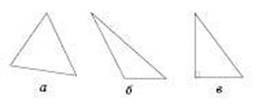
Види трикутників залежно від величини кутів (див. рисунок): а — гострокутний (усі кути гострі); б — тупокутний (один кут тупий); в — прямокутний (один кут прямий).

 

Види трикутників залежно від співвідношення сторін (див. рисунок): а — різносторонній (усі сторони мають різну довжину); б — рівнобедрений (принаймні дві сторони рівні); в — рівносторонній (усі сторони рівні).

 

Прямокутний паралелепіпед

Прямокутний паралелепіпед (див. рисунок) має 8 вершин, 12 ребер, котрі можна розбити на 3 групи по 4 рівних, а також 6 граней (3 пари рівних між собою прямокутників).

 

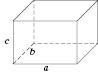
Площа поверхні прямокутного паралелепіпеда дорівнює сумі площ його граней:

𝑆 = 2(𝑎𝑏 + 𝑏𝑐 + 𝑎𝑐)

Об’єм прямокутного паралелепіпеда

𝑉 = 𝑎𝑏𝑐.

Коли 𝑎 = 𝑏 = 𝑐, дістанемо куб (див. рисунок). Усі ребра куба рівні, усі грані — рівні квадрати.

 

 

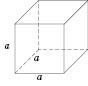
Площа поверхні куба 𝑆 = 6𝑎² .

Об’єм куба 𝑉 = 𝑎³.

№ 54

Довжина однієї із сторін прямокутника дорівнює 14 см, що на 5 см більше за довжину другої сторони. Знайдіть периметр прямокутника. № 55

Прямокутник, сусідні сторони якого дорівнюють 42 см і 14 см, та квадрат мають рівні периметри. Знайдіть сторону квадрата.  № 56

Порівняйте периметри квадрата із стороною 26 см і прямокутника, сторони якого дорівнюють 24 та 16 см.

№ 57

Знайдіть периметр Р та невідомі сторони трикутника, якщо а, в, с – сторони трикутника та вкажіть вид трикутника за сторонами.

         

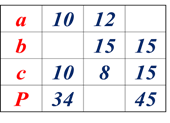
№ 58 ПРАКТИЧНЕ ЗАВДАННЯ.   

1.Побудуйте  довільний трикутник.

2.Запишіть його вершини, сторони, кути.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

№ 59

У 5-А класі – 24 учні, у 5-Б класі – 21 учень, у 5-В класі – 25 учнів. В якому класі всі учні можуть розподілитись на пари без остачі? Чому?

 

№ 60

В садовому центрі можна придбати оптом декілька видів розсади ранніх томатів, які мають різну кількість в упаковці: сорт Євгенія (50 шт), сорт

Аврора (65 шт), сорт Червоне сонечко (73 шт), сорт Маленький принц (68 шт.), сорт Адмірал (60 шт.), сорт Царськосельський (58 шт). Який вид розсади томату треба придбати господарю для висадки, щоб розподілити їх в теплиці без остачі на 5 рядків? 

№ 61

10 піратів знайшли сундук із золотом, який мав вагу 12 376 гр. Скільки грамів золота їм не вистачало для того, щоб розділити золото між собою порівну, і яку кількість золота в такому випадку отримав би кожен пірат?

№ 62

Хлопчикові Івану задали на літо прочитати деяку літературу. Він читає однакову кількість сторінок тричі на день – вранці, в обід та увечері і має у себе наступні книги: Білик І. «Цар, якого вигодувала собака» (71 стор.), Білоус Д. «Чари барвінкові» (53 стор.), Близнець В. «Звук павутинки» (42 стор.), Бордуляк Т.  «Дід Макар» (37 стор.). Яку книжку із запропонованих йому треба прочитати, щоб розпочати вранці одного дня, а закінчити увечері через декілька днів?

№ 63

Шкільна їдальня кожного місяця повинна отримувати певну кількість хлібу. Фірми, які пропонують поставку хлібу до їдальні, підписують договір лише на повний  навчальний  рік, а не помісячно. З урахуванням кількості учнів фірми запропонували школі наступні розміри поставок: Фірма «Пекар» - 30 762 кг хліба, фірма «Хлібобулочні вироби» -

30 815 кг, фірма  «Здоба» - 30 872 кг. Яку фірму обрати, щоб кожного місяця отримувати зручну кількість виробів (1 булка хлібу важить 1 кг). 

 

1.         Найменшим простим числом є число:    а) 1;  б) 2;  в) 3;   г) 4.

2.         Яке парне число є простим?       а) 4;  б) 2;  в) 6;  г) не існує.

3.         Скільки дільників має просте число?      а) один;    б) два;   в) більше двох.

4.         Скільки дільників має складене число?   а) один;    б) два;   в) більше двох.

5.         Число 12:       а) складене;     б) просте.

6.         Число 683:      а) ділиться на 3;    б) просте;   в) ділиться на 9;  г) ділиться на 11.

7.         Яке з даних чисел є простим?    а) 4;  б) 7;  в) 9; г) 15.

8.         Розкладом числа 24 на прості множники є добуток:

          а) 4 ∙ 6;             б) 2 ∙ 12;            в) 2 ∙2 ∙ 3 ∙ 3;           г) 2 ∙ 2 ∙ 2 ∙ 3. 

9.         Яке з даних чисел є складеним?     а)13;      б) 51;     в) 31;     г)17.

10.    Користуючись таблицею простих чисел, вказати, які з чисел 91,  139,  141,  151,  161,  177,  181,  191,  217  є простими.

11.    Знайти серед простих чисел числа “близнюки” ( числа відрізняються одне від одного на 2).                              а) 11 і 13;     б) 5 і 19;     в) 13 і 43;      г) 11 і 17.

12.    Хто перший придумав спосіб знаходження простих чисел? 

       а) Піфагор;    б) Фалес;    в) Ератосфен;     г) Колумб. Середній рівень

1.     Розкладіть на прості множники число:  а) 420;   б) 340;   в) 144;   г) 230;   д)1296.

2.     Назвіть натуральне число, яке не є ні простим, ні складеним.

3.     Що означає : розкласти число на прості множники?

4.     Випишіть спочатку всі прості, а  потім усі складені числа із чисел: 1, 2, 3, 4, 6, 8, 12 і 24.

5.     Назвіть всі дільники кожного з чисел: 2, 3, 5, 7, 11, 13, 17, 19. Скільки дільників має кожне число? Як називають такі числа?

6.     Використовуючи ознаки подільності чисел на 2, на 3 і на 5 доведіть, що слідуючі числа складені: 87, 92, 105, 100, 267, 834, 9282.

7.     Випишіть всі дільники числа і підкресліть прості дільники:

     а) 19;  б) 21;  в) 30;  г) 110;  д) 210.

8.     Випишіть всі дільники чисел: а) 45 і 15;  б) 17 і 25;  в) 70 і 60. Підкресліть однакові дільники.

9.     Простим чи складеним числом є  добуток: а) 23 ∙ 1;  б) 16 ∙ 1; в) 4 ∙ 7; г) 11 ∙ 13 ?  Відповідь обґрунтуйте.

10.Запишіть число, яке має тільки: а) два простих дільники; б) три простих дільники. 

11.Якщо число закінчується цифрою 0, то які прості дільники воно обов’язково має?

12.Якщо сума цифр числа кратна 3, то  який простий дільник воно обов’язково має?

13.Загадка. Я задумав просте число. наступне за ним натуральне число – також просте. Яке число я задумав?   

 

Достатній рівень 

1.         Скільки існує простих парних чисел? Запишіть їх.

2.         Запишіть три послідовні натуральні числа, які є складеними і задовольняють нерівність:  10 <  x < 20. 

3.         Запишіть два прості числа, які задовольняють нерівність:  30 <  т  < 40.

4.         Скільки простих чисел серед чисел, кратних: а) 13;  б) 20 ?

5.         Знайдіть всі прості дільники числа: а) 2005;  б) 1980;  в) 1998;  г) 2004 ;  д) 101 101.

6.         Запишіть найбільше просте число другого десятка чисел.

7.         Запишіть найменше складене число.

8.         Запишіть число: а) 300;  б) 12 000 000 у вигляді добутку степенів простих чисел.

9.         Розкладіть на прості множники числа: а) 4 104;  б) 5 544;  в) 2 004;  г) 2 005.

10.    Запишіть множину натуральних чисел, до 196   включно, кожне з яких можна подати у вигляді добутку двох:  а) однакових множників;  б) однакових простих множників.

11.    Розкладіть кожне число на прості множники і спільні множники винесіть за дужки: а) 18 + 54;  б) 32 + 80;  в) 121 + 99.

12.    При яких значеннях змінної (букви) сума є складеним числом і при яких – простим числом: а) 15 + а;  б) 29 + b; в) 100 + с ?

13.    Знайдіть частку найкоротшим шляхом:   ( 2 ∙ 3 ∙ 5 ∙ 5 ∙  5 ∙ 7  ) : ( 2 ∙ 5 ∙ 5 ∙ 7 ).

14.    Користуючись таблицею простих чисел, дайте відповіді на запитання:  а) Чому тільки одне просте число закінчується цифрою 2?  б) Чому тільки одне  просте число закінчується цифрою 5?  в) Чому немає простих чисел, які закінчуються  цифрами  4,  6,  8,  0?

15.    При яких значеннях а вираз  19а  є простим числом? 

16.    Випишіть дільники добутку, не обчислюючи його: а) а²∙ 3;         б) 2 ∙ 3 ∙ 5.

17.    Випишіть числа, які є дільниками обох добутків:    

     а) 2 ∙ 3 ∙ 7 і  2² ∙ 3;     б)  7 ∙ 5 і 5 ∙ 11;        в) 2² ∙ 3²  і  2  ∙ 3².

18.    Запишіть по два число, кожне з яких розкладається тільки: 

       а) на два однакові прості множники;          б) на два різні прості множники; 

       в)  на три однакові прості множники;         г) на три різні прості множники .

19.    Загадка. Я задумав два простих числа, їх сума – також просте число. Які числа я задумав?

20.    Коли добуток ста простих чисел ділиться на 17?

21.    Які два простих множники завжди містяться в розкладі трицифрового числа, записаного однаковими цифрами?

22.    Знайдіть яке-небудь натуральне число п, щоб число 2^п + 15 було складеним.

23.    Запишіть число 16 ( 14, 10, 12 ) у вигляді суми: 

       а) двох простих чисел;               б) трьох простих чисел.

24.    Знайдіть найменше просте число, яке може бути подане у вигляді суми двох, трьох, чотирьох і п’яти простих доданків.

25.    Запишіть в стрічку одне за одним 10 перших простих чисел в зростаючому порядку. В отриманому багатозначному числі закресліть половину цифр так, щоб число, яке утворене рештою цифр, було:           а) найменшим;           б) найбільшим.

26.    Вставте замість крапок потрібне за змістом слово: 

       … число має більше двох натуральних дільників ( парне, просте, складене, натуральне). 

27.    Виділіть зайве слово:  сімнадцять,   три,   сорок,   два.

28.    Сума двох простих чисел є  непарним  числом. Знайти одне з цих чисел.

29.    Добуток двох простих чисел є парним числом. Знайти одне з цих чисел. Високий рівень

1.         Чи завжди сума двох простих чисел є складеним числом?

2.         Чи завжди різниця двох простих чисел є складеним числом?

3.         Чи може сума двох простих чисел бути простим числом?

4.         Чи може різниця двох простих чисел бути простим числом?

5.         В межах першої сотні знайти всі пари простих чисел, різниця між якими теж просте число.

6.         Чи  може добуток двох простих чисел бути:  а) простим числом;  б) складеним числом?

7.         Чи може добуток декількох простих чисел закінчуватися нулем?  А цифрою 5?

8.         Чи можна знайти чотири різних простих числа, щоб добуток двох з них дорівнював добутку двох інших?

9.         Довести, що серед будь-яких трьох послідовних натуральних чисел простих не більше двох.

10.    Чи може сума трьох послідовних натуральних чисел бути простим числом?

11.    Чи може сума чотирьох послідовних натуральних чисел бути простим числом?

12.    Чи може сума шести простих чисел бути простим числом?

13.    Довести, що серед  чисел будь-якого десятка не більше чотирьох простих.

14.    Чи  можна число 64 подати у вигляді суми трьох простих чисел?

 

 

 

 

 

 

 

 

 

№ 64

Між учнями 6 класу поділили порівну 155 зошитів і 62 ручки. Скільки в цьому класі учнів?

№ 65

Між шкільними бібліотеками поділили 92 тлумачних і 138 орфографічних словників української мови. Скільки було шкіл, якщо відомо,що їх не менше ніж 25 і всі школи отримали однакові комплекти зі словників двох видів?

№ 66

Знайти найбільший спільний дільник (НСД) чисел 24 і 36.

№ 67 Знайти: НСД(36;48); НСД(60;75).

№ 68 Встанови відповідність:

 

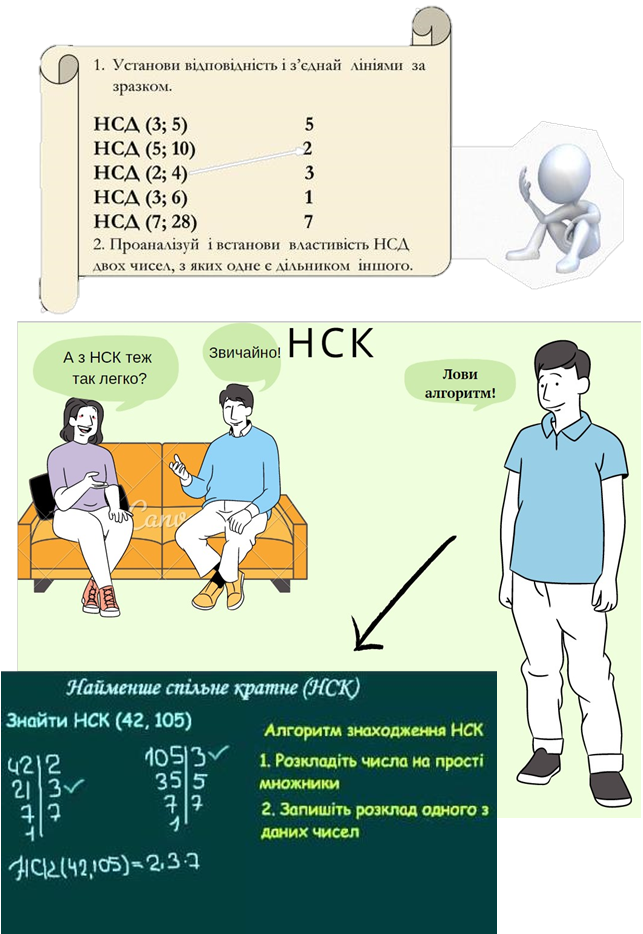
№ 69

Знайти найменше спільне кратне (НСК) чисел 24 и 36.

№ 70 Знайти: НСК(32;48); НСК(14;21).

№ 71

Довжина  кроку Чебурашки дорівнює 15 см, а крокодила Гени – 50 см. Яку найменшу однакову відстань має пройти кожний із них, щоб вони обидва зробили по цілому числу кроків?

№ 72

Марійка ходить до басейну один раз на 3 дні, Юрко – раз на 4 дні, Петрик – раз на 5 днів. Вони зустрілися в басейні у вівторок. Через скільки днів і в який день тижня вони зустрінуться наступного разу?

№ 73 Встановити відповідність:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

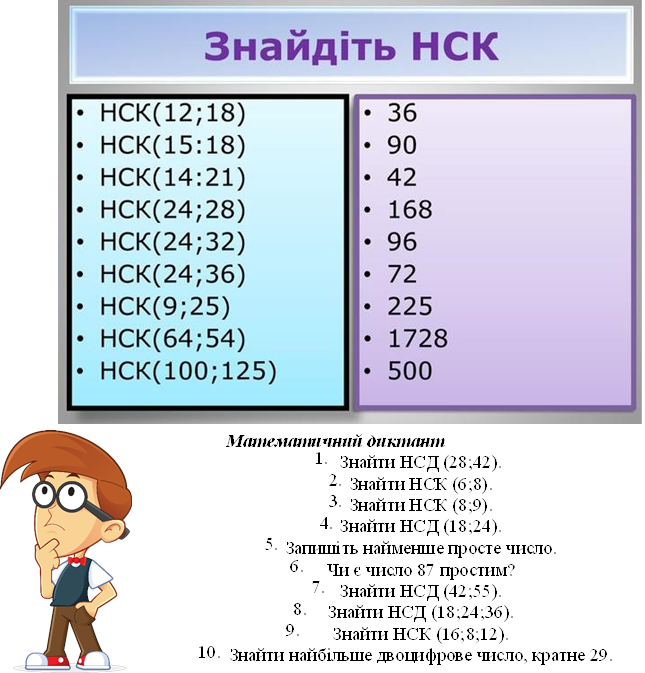
Кінець частини 1