9-кл.Алгебра.Презентація:,,Функція.Область визначення та область значень..''
Про матеріал
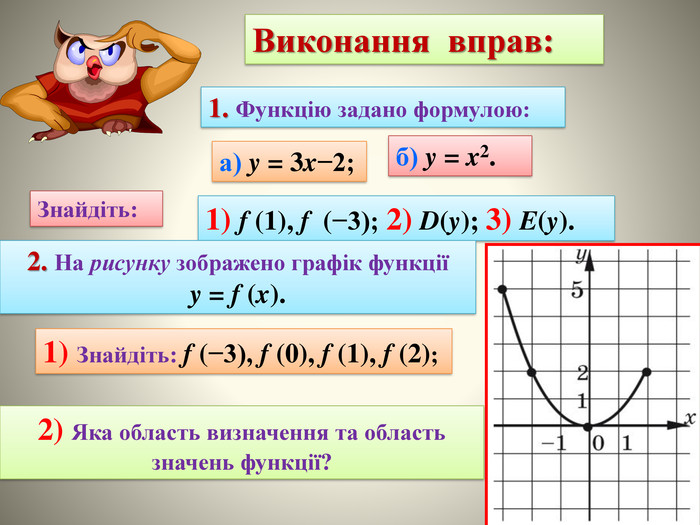
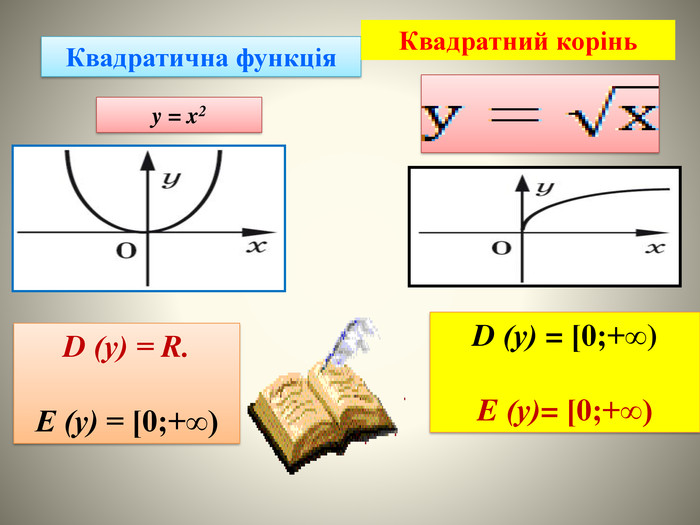
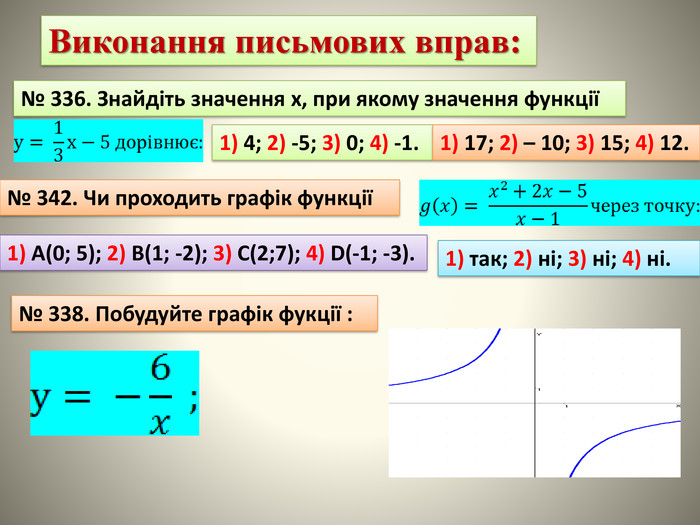
В даній презентації розроблені на основі теоретичних визначень області визначення та області значень показані приклади застосування цих властивостей для дослідження функції.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку















![№ 344 ( 3). Знайдiть область визначення функцiї: Д( у) = (-∞;+∞), крім х = 0; обо х = 3. y = 2x2+1; 0 ≤ x ≤ 1; Знайдiть область визначення функцiї: Д( у) = [ 0; 1]. № 344 ( 3). Знайдiть область визначення функцiї: Д( у) = (-∞;+∞), крім х = 0; обо х = 3. y = 2x2+1; 0 ≤ x ≤ 1; Знайдiть область визначення функцiї: Д( у) = [ 0; 1].](/uploads/files/29885/55507/59618_images/18.jpg)