Алгебра, 7 клас Тема: Добуток різниці на суму двох виразів.
Алгебра, 7 клас
Тема: Добуток різниці на суму двох виразів.
Цілі: сприйняття і первинне закріплення учнями нового матеріалу, зрозуміти зв`язок і відношення між об`єктами вивчення.
Мета уроку: ознайомити учнів з новою формулою скороченого множення; сформувати навички читання і записування формули множення різниці на суму двох виразів (a-b)(a+b)=![]() ; показати застосування даної формули при розв`язуванні інших задач; сприяти формуванню вмінь при застосуванні цієї формули в розв`язуванні різних задач; закріпити раніше вивчений теоретичний матеріал; розвиток математичного мовлення; розвиток вмінь виділяти головне, порівнювати, об`єднувати; формування самостійного мислення.
; показати застосування даної формули при розв`язуванні інших задач; сприяти формуванню вмінь при застосуванні цієї формули в розв`язуванні різних задач; закріпити раніше вивчений теоретичний матеріал; розвиток математичного мовлення; розвиток вмінь виділяти головне, порівнювати, об`єднувати; формування самостійного мислення.
Форми роботи: групова, фронтальна, індивідуальна.
Обладнання: таблиця з кросвордом, карточки для роботи в групах, тестові завдання для роботи в парах, таблиці з формулами скороченого множення для фронтального опитування, проектор.
Хід уроку
І. Вступ. Організаційний момент
Вчитель. Доброго дня. Починаємо наш урок математики. Математика – цікавий предмет. Але його можна добре знати лише завдяки наполегливому навчанню.
Анатоль Франс колись сказав: «Вчитися можна тільки весело…». Хто такий Анатоль Франс відповісте на наступний урок.
Давайте сьогодні на уроці будемо слідувати цим словам. Будьте активні, уважні і з цікавістю вивчайте матеріал уроку, з великим бажанням виконуйте любе завдання.
Представте що ваш клас - науково-дослідний інститут. Ви, учні – співробітники цього інституту. Тут будуть працювати декілька лабораторій для вивчення математичних процесів, які будуть займатися дослідженнями алгебраїчних матеріалів з застосуванням різних формул з використанням нових технологій. На чолі кожної лабораторії є завідувачі. Вони головні консультанти по виконанню дослідницької роботи. (Представляються керівники лабораторій, тобто керівники груп).
Завідувачі лабораторій про результати роботи будуть сповіщати головному відповідальному за виконання дослідницької роботи, тобто вчителю.
Перед початком дослідницької роботи слово надається завідуючим лабораторій. Вони дадуть корисні поради. (Учні підготовлені заздалегідь.)
1-й учень. Йдіть до своєї цілі!
2-й учень. Сприймайте математичні приклади як гру.
3-й учень. Необхідно добре розуміти сенс правил і теорем.
4-й учень. Створіть собі оточення з формул, щоб краще їх запам`ятати, а при можливості застосувати.
5-й учень. Не будь сам. Краще працювати з друзями пліч-о-пліч. Легше і веселіше йти разом до своєї цілі.
Учитель. Постійно контролюйте свої дії, тобто постійно перевіряйте правильність виконання математичних операцій. І успіх буде забезпечений.
Тема нашої дослідницької роботи: Добуток різниці на суму двох виразів. Які цілі ви поставили перед собою?
Учні називають:
- Добуток суми на різницю двох виразів за правилом множення многочленів.
- Дізнатись, що утвориться після множення суми і різниці двох виразів і застосувати цей спосіб множення до розв`язання інших задач.
ІІ. Актуалізація опорних знань
1. Розгадування кросворду.
Учитель. Щоб працювати над дослідницькою роботою потрібна теорія. Перевіримо за допомогою математичного кросворда.
По горизонталі:
1. Символ, за допомогою якого записують натуральні числа. (Цифра)
2. Вираз ![]() . (Многочлен)
. (Многочлен)
3. Значення змінної при якій рівняння перетворюється в правильний вираз. (Корінь)
4. Степінь многочлена ![]() . (Вісім)
. (Вісім)
5. Залежність однієї змінної від іншої. (Функція)
6. Вираз, який має добуток чисел, змінних та їх степенів. (Одночлен)
7. Графік функції у = ![]() . (Парабола)
. (Парабола)

Вчитель. Яке слово отримали по вертикалі? (Формула).
Що про це слово знаємо?
Які формули вивчили на попередніх уроках?
2. Обчислити:
А) ![]()
Б) ![]()
В) ![]()
Г) ![]()
3. Підставте невідомий одночлен:
А) ![]() 9 + ? +
9 + ? +![]() (6m).
(6m).
Б) ![]() 14ac + ?; (49
14ac + ?; (49![]() ).
).
4. Біля доши:
-
Піднесіть до квадрату одночлен 7
 .
.
- Різницю квадратів 2d і 5k.
- Квадрат різниці 12х і 18у.
-
Помнож на 3 одночлен 19
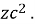
- Добуток двох сум 7х і 3, 2х і 1.
- Добуток різниці а і в на їх суму.
Учні обмінюються зошитами та перевіряють роботи один одного. При перевірці останнього 6) завдання виникає питання у дітей до вчителя.
ІІІ. Формування теми та мети уроку.
IV. Формування знань
1. Постановка проблеми і її вирішення колективним способом.
Вчитель. Вираз (а-в)(а+в) являється предметом нашого дослідження. Потрібно помножити різницю двох виразів на їх суму. В кожної лабораторії є план роботи на карточці. Працювати потрібно разом. Використовуйте теоретичні знання, виконуйте деякі перетворення, приложіть максимум зусиль і обов`язково у вас все вийде.
Прочитайте план роботи.
На карточці написано.
- Помножити різницю а –в на суму а – в;
- Зведіть подібні доданки, якщо вони є;
- Запишіть вираз який утворився;
- Зробіть висновок, чому дорівнює добуток різниці і суми двох виразів.
2. Висновок зробленого завдання
Добуток різниці двох виразів на їх суму дорівнює різниці квадратів цих виразів. Записали в зошит.
(а-в)(а+в)=![]()
Перевірка даної формули.
Вчитель: перевіримо дану формулу з іншими одночленами. Учень біля дошки розв`язує.
(2х-3)(2х+3)=4![]()
Отже, формула справедлива і для інших одночленів.
(а-в)(а+в)=![]()
Отримана формула теж є формулою скороченого множення.
(Вчитель вивішує ще одну таблицю з формулою. І зачитують правила в підручнику.)
V. Закріплення знань. Відпрацювання вмінь.
1. Робота біля дошки з коментуванням
(3х-7у)(3х+7у)=
(![]()
2. Робота в групі з перевіркою.
Підручник №№
Вчитель: перед тим як почати виконувати номер з підручника, порівняйте, чим відрізняються вирази
(а-в)(а+в)=![]()
(а+в)(а-в)=![]()
(а-в)(в+а)=![]()
В 2 виразі переставлені множники, використовується властивість множення. В 3 виразі використовується властивість додавання в других дужках.
Отже, всі три вирази рівні, а тому = ![]() , так як виконувалися згідно математичних законів.
, так як виконувалися згідно математичних законів.
3. Пояснення геометричного зміст даної формули.
(а-в)(а+в)=![]()
Робота проводиться в групах (з перевіркою).
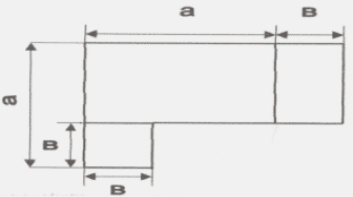
Площа прямокутника зі сторонами а-в і а+в дорівнює площі квадрата зі стороною а мінус площа квадрата зі стороною в.
4. Колективна робота
В групах виконується №№ . В цей же час за дошкою учень виконує цей же номер, потім робиться перевірка. Другий учень грає біля дошки в ігру «Найди пару». В нього є карточки. На одних з них записана ліва частина виразу, на другій права. Учень повинен з`єднати 2 карточки так, щоб виконувалась рівність.
-
 =
= 
-
(0,7х -
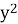 )(0,7х +
)(0,7х +  = 0,49
= 0,49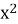 -
- 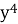
-
 = 0,49х
= 0,49х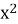 +1,4х
+1,4х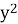 +
+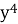
-
 =
= 
-
 (
( )=
)= 
Учень залишає тільки ті вирази, які відповідають темі уроку.
VІ. Підсумок уроку
Вчитель. Яка проблема стояла перед нами сьогодні? Яке відкриття сьогодні зробили?
Отже, сьогодні ви отримали нову формулу скороченого множення.
(а-в)(а+в)=![]() , а також застосовували цю формулу при множенні двочленів. Це була головна мета нашого уроку.
, а також застосовували цю формулу при множенні двочленів. Це була головна мета нашого уроку.
Оцінки.
VІІ. Домашнє завдання
Опрацювати параграф в підручнику ___ , виконати №№_____


про публікацію авторської розробки
Додати розробку
