Алгоритм розв'язування задач на застосування принципу суперпозиції полів

Електростатика.   Алгоритм розв’язування задач на застосування принципу суперпозиції полів

1. Уважно прочитати умову задачі та зробити короткий запис. Провести аналіз умови задачі. Записати   необхідні   табличні   дані  та  значення фундаментальних констант. При цьому всі числові значення величин повинні бути виражені в основних одиницях міжнародної системи одиниць (SI).
2. Зробити малюнок, на якому вказати знаки зарядів,  напрям вектора напруженості електричного поля, створеного кожним із зарядів у даній точці та обрати осі координат.
3. Записати принцип суперпозиції полів у векторній формі:

Знайти векторну суму напруженостей, користуючись правилом додавання векторів.

4. За формулою напруженості електричного поля точкового заряду записати вирази для кожного з доданків та підставити їх в одержану в п.3 формулу.
5. Розв’язати одержане рівняння відносно шуканих величин.
6. Перевірити одиниці вимірювання фізичних величин.
7. Підставити числові значення.
8.  Оцінити реальність одержаного результату.

Задача. Знайти напруженість Е електричного поля в точці, яка лежить посередині  між точковими зарядами q₁=8 нКл і q₂= 6 нКл у вакуумі. Відстань між зарядами r=10 см.

1. Уважно прочитати умову задачі та зробити короткий запис. Провести аналіз умови задачі. Записати   необхідні   табличні   дані  та  значення фундаментальних констант. Виразити значення фізичних величин в міжнародній системі одиниць(SI).

 2. Зробити малюнок, на якому вказати знаки зарядів,  напрям вектора напруженості електричного поля, створеного кожним із зарядів у даній точці та обрати осі координат.

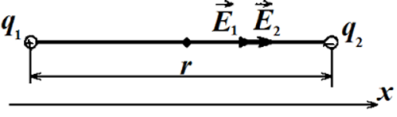
Враховуючи те, що вектор напруженості напрямлений від позитивного заряду, але до негативного, визначаємо напрям обох векторів ₁ та _{2 .} В даному випадку обидва вектори напрямлені вправо. Достатньо обрати одну вісь ОХ, спрямувавши її вправо.

3.    Записати принцип суперпозиції полів у векторній формі:

 . Знайти векторну суму напруженостей, користуючись правилом додавання векторів.     

Згідно з принципом суперпозиції полів, напруженість електричного поля в даній точці дорівнює геометричній сумі відповідних напруженостей:         .     Або в проекції на вісь OX:    Е=Е₁+Е_2.

4. За формулою напруженості електричного поля точкового заряду записати вирази для кожного з доданків та підставити їх в одержану в п.3 формулу.

Напруженість електростатичного поля точкового заряду у вакуумі

, де R – відстань від заряду до точки, в якій визначаються напруженість. За умовою точка знаходиться посередині, тому R₁=R₂=r/2. Отже, сумарна напруженість електричного поля:

 5. Розв’язати одержане рівняння відносно шуканих величин.               

В даній задачі достатньо спростити одержану формулу:

6. Перевірити одиниці вимірювання фізичних величин.

, що і потрібно було одержати.

7. Підставити числові значення.

=5,04·10⁴ (В/м)=50,4 кВ/м.

8. Оцінити реальність одержаного результату та записати відповідь.

Отриманий результат цілком реальний та задовольняє умову задачі.

Відповідь:  Е=50,4 кВ/м.