Підготовка до контрольної роботи 

Тема. Системи лінійних рівнянь з двома змінними

1. ° Розв’яжіть методом підстановки систему рівнянь:

1)     Виразимо з першого рівняння системи (1) змінну х через змінну у:

2)     Підставимо в друге рівняння системи замість х вираз :

3)     Розв’яжемо друге рівняння системи (2):

4)     Знайдемо відповідне значення х:

Отже, (2; -2) — розв’язок системи.

2.     ° Розв’яжіть методом додавання систему рівнянь:

Додамо почленно ліві й праві частини рівнянь і отримаємо рівняння з однією змінною:  

Замінимо перше рівняння системи (1) рівнянням . Одержимо систему:

. Системи (1) і (2) рівносильні. Розв’яжемо систему (2). 

З першого рівняння маємо:  

Підставивши це значення у друге рівняння системи (2), отримаємо:

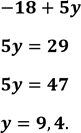
Пара (-9; 9,^[1]) — розв’язок системи

3.     Розв’яжіть графічно систему рівнянь:

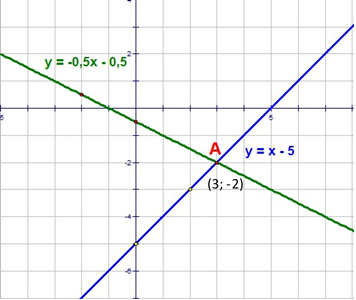Побудуємо в одній системі координат графіки обох рівнянь системи. Графіком рівняння  є пряма,

яка проходить через точки

Графіком рівняння  

 є пряма, яка

проходить через точки

Відповідь: (3; -2)

Розв’язання

Нехай швидкість першого пішохода х км/год, а швидкість другого – у км/год. Тоді перший пройшов до зустрічі 3х км, а другий 3у км. Відстань між селищами 30 км. Маємо перше рівняння: 3х + 3у = 30.

За умовою задачі один із пішоходів пройшов до зустрічі на 6 км більше, ніж другий. Маємо друге рівняння: 3х – 3у = ^[2].

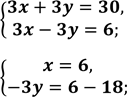
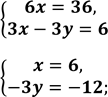
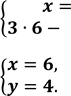
Складемо і розв’яжемо систему : 

Відповідь: швидкість першого пішохода 6 км/год, швидкість другого пішохода –  4 км/год

5. Розв’яжіть систему рівнянь:

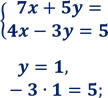
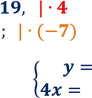
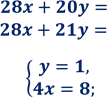
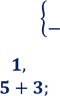
1)                                                                                                                                                                                                                                  

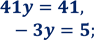
Відповідь: (2; 1)

              2)              

Якщо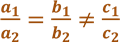 , то система розв’язків немає

Відповідь: розв’язків немає

Маємо .    Відповідь: