"Числові множини натуральних та цілих чисел"


ЧИСЛОВІ МНОЖИНИ
8 клас
(ЧАСТИНА 1)
![]()

ЗМІСТ
Вступ
Частина І. Елементи теорії множин.
- Множина та її елементи.
- Підмножина. Рівні множини.
- Операції над множинами.
- Скінченні множини.
- Еквівалентність та потужність множин. Декартів добуток множин.
- Числові множини (Множина натуральних і цілих чисел).
Список рекомендованої літератури.
Частина ІІ. Основи теорії подільності. Множина простих чисел.
- Подільність націло та її властивості.
- Ділення з остачею. Конгруенції та їх властивості.
- Найбільший спільний дільник, найменше спільне кратне двох натуральних чисел.
- Прості і складені числа.
- Ознаки подільності чисел.
- Властивості простих чисел.
- Розкладання на множники.
- . Лінійні діофантові рівняння.
- . Розгляд проблем, пов’язаних з простими та досконалими числами.
Список рекомендованої літератури.
Вступ
Даний збірник пропонується під час підготовки учнів до олімпіад використовувати елементи підготовчого курсу «Розв’язування олімпіадних задач», який має на меті: сприяти досягненню учнями високого рівня математичної підготовки; розвивати стійкий пізнавальний математичний інтерес; поєднати шкільне навчання з дослідницькою діяльністю за вибором, згідно з власним інтересом до конкретних проблем.
Цілі та завдання:
- підвищення рівня якості знань учнів, розширення математичногокругозору;
- прищеплення інтересу до математики та її застосувань;
- виявлення найбільш обдарованих учнів та розвиток їх творчих здібностей;
- навчання культурі самоосвіти та саморозвитку школярів;
- удосконалення умінь та навичок самостійної роботи учнів зі спеціальної літератури;
- організація діяльності учнів з метою підготовки їх до участі в різних олімпіадах та конкурсах;
- профорієнтація учнів та підготовка їх до отримання подальшої освіти.
Основні напрямки роботи:
- підготовка учнів до оволодіння знаннями, що виходять за межі шкільної програми;
- навчання учнів роботі з додатковою та спеціальною літературою;
- організація групових та індивідуальних консультацій;
- підготовка, організація та проведення турнірів, олімпіад;
- підготовка учнів до участі в олімпіадах та конкурсах.
ЧАСТИНА І. ЕЛЕМЕНТИ ТЕОРІЇ МНОЖИН
- МНОЖИНА ТА ЇЇ ЕЛЕМЕНТИ
 Основи теорії множин були закладені відомим німецьким математиком Георгом Кантором і другій половині минулого століття. Сьогодні теорія множин - це математична теорія, на якій ґрунтується більшість розділів сучасної математики. В шкільному курсі математики теорія множин розглядається при поглибленому вивченні математики у 8 класі. Вивчення цієї теми дозволяє
Основи теорії множин були закладені відомим німецьким математиком Георгом Кантором і другій половині минулого століття. Сьогодні теорія множин - це математична теорія, на якій ґрунтується більшість розділів сучасної математики. В шкільному курсі математики теорія множин розглядається при поглибленому вивченні математики у 8 класі. Вивчення цієї теми дозволяє
математично обґрунтовано вводити такі поняття як «область визначення виразу», «множина раціональних виразів», а в подальшому визначати множину розв’язків
Георг Кантор нерівності.
1845-1918
Поняття множини належить до числа основних, невизначених понять математики. В теорії множин поняття "множина" належить до первинних невизначальних понять, тобто воно не може бути означено через інші більш прості терміни або об'єкти, а пояснюється на прикладах, апелюючи до нашої уяви та інтуіції. Такими поняттями в математиці є також поняття "число", "пряма", "точка", "площина" тощо.
Прикладами множин можуть служити: множина десяткових цифр, множина літер українського алфавіту, множина мешканців Києва, множина парних чисел, множина розв'язків деякого рівняння та ін.
На письмі множини позначаються, як правило, великими літерами. Для деяких множин у математиці вживаються сталі позначення. Наприклад, Z - множина цілих чисел, N - множина натуральних чисел, Q - множина раціональних чисел, R- множина дійсних чисел тощо.
Об'єкти, з яких складається задана множина, називаються її елементами. Елементи множин позначатються малими літерами латинського алфавіту. Той факт, що об'єкт a є елементом множини M записується так: a![]() M, якщо деякий елемент a не належить множині M, вживають позначення a∉M. Наприклад, 5
M, якщо деякий елемент a не належить множині M, вживають позначення a∉M. Наприклад, 5 ![]() N, але
N, але ![]() ∉N,
∉N, ![]() ∉N, але
∉N, але ![]() ∊R.
∊R.
Множина - це сукупність об’єктів , як об’єднані в сукупність за певною ознакою (є спеціальні назви)
Множина є заданою, якщо є задана характеристика об’єктів множини.
ℕ - множина натуральних чисел,
ℤ - множина цілих чисел,
ℚ - множина раціональних чисел,
ℝ - множина дійсних чисел,
ℂ - множина комплексних чисел.
Кожний об’єкт, що входить до множини А, називається елементом цієї множини.
Зазвичай елементи позначають малими латинськими літерами: a, b, c, d тощо.
Умовні позначки.
∈ - знак належності для елементів множини
∉ - знак неналежності для елементів множини
⊂ - знак включення для множин
∪ - знак об’єднання для множин
∩ - знак перетину (перерізу) для множин
∅ - порожня множина
Якщо a належить множині A, то пишуть a ∈ A (читають: «a належить множині A»). Якщо b не належить множині A, то пишуть b ∉ A (читають: «b не належить множині A»).
Множина, що не містить жодного елемента, називається порожньою множиною і позначається ∅.
Дві множини A і B називають рівними, якщо вони складаються з одних і тих самих елементів, тобто кожний елемент множини Aналежить множині B, і навпаки, кожний елемент множини B належить множині A.
Якщо множини A і B рівні, то пишуть A = B.
З означення випливає, що множина однозначно визначається своїми елементами.
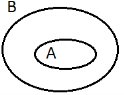
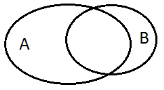
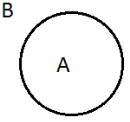
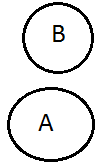
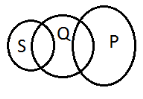
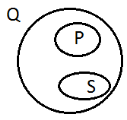
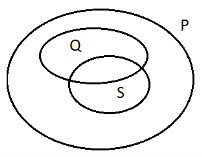
Для ілюстрації співвідношень між множинами використовують схеми, які називають діаграмами (кругами) Ейлера-Венна.
СПОСОБИ ЗАДАННЯ МНОЖИНИ
Існують два основних способи задання множини.
Перший спосіб задає множину переліком її елементів.
Цим способом особливо часто задаються скінченні множини. Наприклад, множина учнів класу задається їхнім списком. Множина, що складається з елементів a, b, c, ..., d, позначають за допомогою фігурних дужок: А = {a; b; c; ...; d}. Множина коренів рівняння ![]() складається з двох чисел 4 і -4: А={4; -4}. Множина цілих розв’язків нерівності -2 <х <3 складається з чисел -1, 0, 1, 2, тому В= {-1,0,1,2}.
складається з двох чисел 4 і -4: А={4; -4}. Множина цілих розв’язків нерівності -2 <х <3 складається з чисел -1, 0, 1, 2, тому В= {-1,0,1,2}.
Зрозуміло, що не будь-яку множину можна задати у такий спосіб, тому множини задаються характеристичною властивістю елементів множини, тобто такої властивості, яку мають усі елементи даної множини і тільки вони.
Другий спосіб задання множини є вказівкою властивості її елементів.
Множину елементів х, що володіють даною характеристичною властивістю Р (х), також записують за допомогою фігурних дужок: Х = {х | Р(х)}, і читають: множина Х складається з елементів х, таких, що виконується властивість Р(х).
Наприклад, вище згадані множини можна задати використовуючи характеристичну властивість: А={х|![]() }, В = {х | -2 <х <3, х
}, В = {х | -2 <х <3, х ![]() Z}. Якщо характеристичною властивістю, що визначає множину М, не володіє жоден об'єкт, тоді кажуть, що множина М - порожня (не містить жодного елементу) і пишуть: М=Ø.
Z}. Якщо характеристичною властивістю, що визначає множину М, не володіє жоден об'єкт, тоді кажуть, що множина М - порожня (не містить жодного елементу) і пишуть: М=Ø.
Наприклад, М = {х | ![]() , х
, х ![]() R} - множина дійсних чисел х, таких, що
R} - множина дійсних чисел х, таких, що ![]() , - порожня множина, тому що таких дійсних чисел не існує. Множина К={Ø} не є порожньою, тому що містить один елемент – порожню множину.
, - порожня множина, тому що таких дійсних чисел не існує. Множина К={Ø} не є порожньою, тому що містить один елемент – порожню множину.
Елементами множини можуть виступати і самі множини. Вірним є твердження {а}∊{{а}}, {а}∉{а, d}.
Задачі для самостійного розв’язування.
1. М – множина музичних інструментів естрадного оркестру. Чи належить цій множині:
а) барабан; б) гітара; в) струна гітари; г) балалайка?
2. З яких елементів складається множина предметів, які вивчають у 8 класі школи?
3. А - множина геометричних фігур на площині. Чи належить цій множині:
а) п’ятикутник; б) пряма; в) куб; г) коло; д) точка?
4. Множину букв українського алфавіту позначили буквою С. Указати серед наступних висловлювань істинні:
а) б ∈ С; б) ю ∈ С; в) z ∈ С; г) t ∈ С; д) 33 ∈ С.
5. Назвати 5 чисел, що належать множині натуральних чисел. Чи правильно, що
а)15 ∈ N; б)⅔ ∈ N; в) 17,5 ∈ N; г) -37 ∈ N; д) 13457 ∈ N?
6. N – множина натуральних чисел, К – множина парних натуральних чисел, М – множина натуральних чисел, кратних 3. Записати, використовуючи символ ∈, яким з даних множин належать числа 4, 12, 79, 5/6.
7. М – множина точок кола. Назвати точки, що
1) належать колу,
2) не належать колу.
Вияснити, які з наступних висловлювань істинні:
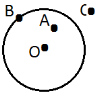 а) О ∈ М; б) А ∉ М; в) В ∈ М; г) С ∉ М.
а) О ∈ М; б) А ∉ М; в) В ∈ М; г) С ∉ М.
8. К – множина точок круга. Назвати точки, що:
а) належать кругу;
б) не належать кругу;
в) належать кругу, але не належать колу.
9. Х – множина класів школи. Чи є елементом цієї множини учень даної школи?
10. Елементами множини Y є множини букв:
Y={{а, б}, {к, с, н}, {о, п, р, ю}}.
 Чи правильно, що:
Чи правильно, що:
а) {к, с, н} ∈ Y;
б) а ∈ Y;
в){о, п} ∉ Y;
г){а, б} ∉ Y?
Способи задання множин
11. Задані множини:
А – множина частин світу;
В – множина океанів на земній кулі;
С – множина місяців року;
М – множина букв у слові «паралелограм»
а) Сформулювати характеристичну властивість елементів кожної з даних множин.
б) Задати дані множини переліком їх елементів.
12. Вияснити, яка характеристична властивість елементів множини, і перелічити її елементи:
а) множина однозначних чисел;
б) множина натуральних дільників числа 24;
в) множина двозначних чисел, які діляться на 10.
13. Задані множини:
А={1,3,5,7,9}, В={12,11,10,9,8,7}, С={11,22,33,44,55,66,77,88,99}.
Сформулюйте характеристичну властивість елементів кожної множини.
14. Прочитати записи і перелічити елементи кожної множини:
А={х/ х ∈ N, х<3};
В={х/ х ∈ N, 1<x<3};
С={х/ х ∈ Z0, х<3,5}; D={х/ х ∈ Z, -5 < x ≤ 2}; E={x/ x ∈ Z, -7 ≤ x ≤ -2}.
15. З’ясувати, які цілі числа є елементами множин К, Р і М, якщо:
К={у/у+5=9}; Р={х/х(х+2)=0}; М={х/4(3х-7)=-28+12х}.
16. Яка множина задана в кожному з випадків:
а) множина міст на Місяці;
б) множина динозаврів у зоопарку;
в) множина натуральних чисел, менших нуля;
г) множина розв’язків рівняння 3(х+2)=8+3х;
д) множина трикутників зі сторонами довжиною 4см, 5см, 10см.
2. ПІДМНОЖИНА. РІВНІ МНОЖИНИ.
Над множинами, як і над багатьма іншими математичними об'єктами, можна робити різні операції, які іноді називають теоретико-множинними операціями. Слід враховувати, що у результаті операцій з вихідних множин виходять нові.
Нехай А та В - дві множини. Якщо кожен елемент множини А є елементом множини В, то говорять, що множина А є підмножиною множини В і пишуть: А ⊂ B або B ⊃ A. Отже, 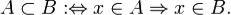
Наприклад: N 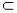 Z
Z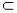 Q
Q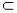 R.
R.
Знаки включення ⊂ або ⊃ відносяться ![]() тільки до множин, їх не слід змішувати зі знаками приналежності ∊. Порожню множину вважають підмножиною будь-якої множини М, тобто Ø∊М, якою б не була множина М. Зрозуміло, що кожна множина є підмножиною самої себе: М⊂М.
тільки до множин, їх не слід змішувати зі знаками приналежності ∊. Порожню множину вважають підмножиною будь-якої множини М, тобто Ø∊М, якою б не була множина М. Зрозуміло, що кожна множина є підмножиною самої себе: М⊂М.
Наприклад, випишіть усі підмножини множини A = {a, b, c}. Маємо: {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}, ∅.
Якщо для двох множин А і В одночасно мають місце два включення А⊂В і В⊃А, тобто А є підмножиною множини В і В є підмножиною множини А, то множини А і В складаються з одних і тих же елементів. Такі множини А і В називають рівними і пишуть: А = В.
Наприклад, якщо А={2; 3}, а В={х| х2-5х+6=0}, то А=В.
Якщо А⊂В, але А ≠ В, тобто існує хоча б один елемент множини В, не належить А, то говорять, що А є власною підмножиною множини В.
Розглянемо множину, яка містить в якості своєї підмножини будь-яку іншу множину. Таку «всеосяжну» множину будемо називати універсальною і позначати буквою U.
Якщо кожен елемент однієї множини A є елементом другої множини B, то кажуть, що перша множина A є підмножиною другої множини B і записують так: A ⊂ B.
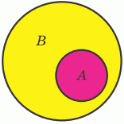
Використовують також запис A ⊆ B, якщо множина A або є підмножиною множини B, або дорівнює множині B.
Задачі для самостійного розв’язування.
1. Вияснити, в якому відношенні знаходиться кожна пара множин:
а) A={m,n,p} і B={k,n,m};
б) A={m,n,p} і B={m,n,p,k};
в) A={m,n,p} і B={p,m,n};
г) A={m,n,p} і B={k,l}.
2. К – множина приголосних букв українського алфавіту, Р={б,в,г,д,є}. В якому відношенні знаходяться множини К і Р? Зобразити дані множини за допомогою кругів Ейлера.
3. Задані множини: А – множина букв українського алфавіту, В – множина голосних букв. Довести, що В є підмножиною множини А. Як зобразити дані множини за допомогою кругів Ейлера?
4. Відомо, що x ∈ X і x ∈ Y. Чи випливає звідси, що
а) Х є підмножиною множини Y;
б) Y є підмножиною множини X;
в) Х=Y?
5. Учень встановив, що кожний елемент множини Х належить множині Y. Вияснити, який з наступних висновків повинен був зробити учень:
а) Х є підмножиною множини Y;
б) Y є підмножиною множини X;<
в) Х=Y?
6. Відомо, що a ∈ N. Чи можна стверджувати, що a ∈ Z? Чи є правильним обернене твердження: з того що a ∈ Z, випливає, що a ∈ N?
7. Учень довів,що будь – який елемент множини Р належить множині Q і, навпаки, будь – який елемент множини Q належить множині Р. В якому відношенні знаходяться множини Р і Q? 24. Задана множина С={-4,8; -3; 0; 0,5; 8,3; 9; 12}. Виділити її підмножину, елементами якої є:
а) натуральні числа;
б) цілі числа;
в) парні натуральні числа;
г) цілі невід’ємні числа;
д) цілі числа, кратні 3;
е) додатні числа.
8. На рисунку 1 зображені діаграми множин А і В. Вияснити, яке відношення між множинами А і В у кожному з даних випадків, і наведіть приклади множин А і В.
9. Відомо, що D – множина дерев у саду, F – множина фруктових дерев у цьому саду, К – множина яблунь у саду. Встановити, які відношення між парами цих множин, якщо всі вони не порожні. Зобразити множини D, F і K за допомогою кругів Ейлера.
10. Побудуйте круги Ейлера для множин Е, К і М, якщо:
Е – множина двоповерхових будинків у місті;
К – множина п’ятиповерхових будинків у місті;
М – множина будинків у місті.
11. Задані множини:
Р – множина рівносторонніх трикутників;
Q - множина рівнобедрених трикутників;
S - множина рівнобедрених прямокутних трикутників.
Указати, на якому рисунку зображені дані множини. (рисунок2)
|
Рисунок 1. |
|||
|
|
|
|
|
|
а) |
б) |
в) |
г) |
|
Рисунок 2. |
||
|
|
|
|
|
а) |
б) |
в) |
12. М – множина цифр у запису числа 923923,
К – множина цифр у запису числа 3222329.
Вияснити, яке висловлювань істинне:
а) множина М є підмножиною множини К;
б) множина К є підмножиною множини М;
в)множини М і К перетинаються.
13. А – множина правильних многокутників,
В – множина чотирикутників,
М – множина прямокутників.br/ Установити відношення, які існують між даними множинами А, В. М; зобразіть їх за допомогою кругів Ейлера.
14. Задані множини:
А – множина паралелограмів, В – множина ромбів, С – множина прямокутників.
а) установити відношення, які існують між даними множинами, і зобразити їх за допомогою кругів Ейлера.
б) указати серед тверджень істинні:
Будь – який ромб є паралелограмом.
Будь – який ромб є прямокутником.
Деякі ромби є прямокутниками.
Деякі ромби не є прямокутниками.
Всі ромби не є прямокутниками.
15. Довести, що наступні множини рівні:
Р – множина остач від ділення будь – якого натурального числа на 7;
А={x |x ∈ Z0; х<7}
В={5,2,6,3,1,4,0}.
33. Назвати серед даних множин рівні:
А={x| x ∈ Z, 0<x<4}; D={x| x ∈ Z, 0<x<5};
B={x| x ∈ Z, 0<x<5}; F={x| x ∈ Z, 0<x<4};
C={3,1,2}; R={x| x ∈ Z, 0<x<4}.
16 Розв’язати рівняння:
а) (2х-4)(7-х)=0;
б) х(2-х)(3х-21)=0;
в) (х-2)(х-7)=0.
Указати рівняння, множини розв’язків яких рівні. Як називаються такі рівняння?
- ОПЕРАЦІЇ НАД МНОЖИНАМИ
Розглянемо промені АВ і ВА зображені на рисунку.
![]()
Множина точок, що належать і променю АВ, і променю ВА є множина точок відрізка АВ. Таким чином, точки відрізка АВ належать обом вище вказаним множинам. Множина, що складається з елементів, що належать і множині А, і множині В, називається перетином множин, позначається: А∩В.
![]() .
.
Наприклад, ![]() , тоді
, тоді
![]() ,
, ![]() .
.
За допомогою діаграм Ейлера-Венна зобразимо перетин множин, що не мають жодного спільного елемента: А∩В=Ø;
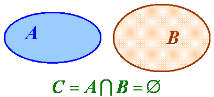
та перетин множин, що мають спільні елементи:
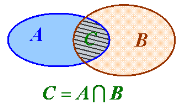
Розглянемо множину точок променів АВ і ВА. Усі точки що належать променю А і променю ВА називають об´єднанням множин: позначається: А![]() В.
В.
![]() .
.
Наприклад, ![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]() .
.
Приклади:
{1, 2} ∩ {червоний, білий} = ∅
{1, 2, зелений} ∩ {червоний, білий, зелений} = {зелений}
{1, 2} ∩ {1, 2} = {1, 2}
Приклад 2.
Нехай А - множина всіх дільників числа 32, В - множина всіх дільників числа 24. Отже,
А = {1, 2, 4, 6, 8, 16, 32}, В= {1, 2, 3, 4, 6, 8, 12, 24}.
Тоді
С = А ![]() В, С = {1, 2, 4, 8}.
В, С = {1, 2, 4, 8}.
 Деякі властивості перетину:
Деякі властивості перетину:
A ∩ B = B ∩ A
A ∩ B ⊆ A
A ∩ A = A
A ∩ ∅ = ∅
За допомогою діаграм Ейлера-Венна зобразимо об´єднання множин, що не мають жодного спільного елемента: А∩В=Ø;

та об´єднання множин, що мають спільні елементи:
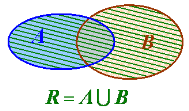
Приклади:
{1, 2} ∪ {червоний, білий} = {1, 2, червоний, білий}
{1, 2, зелений} ∪ {червоний, білий, зелений} = {1, 2, червоний, білий, зелений}
 {1, 2} ∪ {1, 2} = {1, 2}
{1, 2} ∪ {1, 2} = {1, 2}
Деякі властивості операції об'єднання:
A ∪ B = B ∪ A
A ⊆ A ∪ B
A ∪ A = A
A ∪ ∅ = A
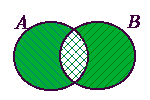 Різницею множин А і В назвемо множину, що складається з таких елементів множини А, яких не містить множина В:
Різницею множин А і В назвемо множину, що складається з таких елементів множини А, яких не містить множина В:
![]() .
.
Наприклад, ![]()
![]() , тоді
, тоді
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
За допомогою діаграм Ейлера-Венна зобразимо різницю множин А\В та В\А:

Приклади:
{1, 2} − {червоний, білий} = {1, 2}
{1, 2, зелений} − {червоний, білий, зелений} = {1, 2}
{1, 2} − {1, 2} = ∅
А = {5, 6, 8, 12}, В = {5, 6}, D = А\В = {8, 12}.
А = {5, 6}, В = {5, 12, 6}, D = А\В = ![]() .
.
Якщо A ⊂ U, то елементи множини U, які не належать А, називаються доповненням множини А до множини U і позначають як CUA або UCA.Якщо U - множина цілих чисел, то доповнення її підмножини A всіх парних чисел є підмножина В всіх непарних чисел.
 Деякі властивості операції доповнення:
Деякі властивості операції доповнення:
A ∪ A′ = U
A ∩ A′ = ∅
(A′)′ = A
A − B = A ∩ B′
Задачі для самостійного розв’язування.
1. Знайдіть перетин множин А і В, C і D, якщо А={х| х>3, x∊N}, B={х| х≤9, x∊N}, С={(х;y)| 2x+y=4}, D={(х;y)| x - y=5}.
2. Знайдіть об´єднання множин А і В, якщо А={х| х2-4=0}, B={х| (х-3)(х+2)=0}.
Знайдіть А![]() В
В![]() С А
С А![]() С
С![]() В А\В
В А\В![]() С, якщо А={-1; 0; 1; 2; 3; 4}, B={-3; -2; -1; 0; 1}, С={3; 4; 5; 6; 7}.
С, якщо А={-1; 0; 1; 2; 3; 4}, B={-3; -2; -1; 0; 1}, С={3; 4; 5; 6; 7}.
3. Нехай А - множина всіх прямокутників, В - множина всіх ромбів. Знайдіть А ∩ В.
4. Нехай А - множина всіх рівнобедрений трикутників, В - множина всіх рівносторонніх трикутників. Знайдіть А ![]() В.
В.
5. Х={0; 1; 3; 5}, Y={1; 2; 3; 4}. Знайти: Х ∪ Y. ({0; 1; 2; 3; 4; 5}).
6.Знайти об’єднання множини учнів школи, молодших 12 років і множини учнів цієї школи, старших 10 років. (множина всіх учнів цієї школи).
7. Знайти об’єднання гострокутних, тупокутних і прямокутних трикутників. (множина всіх трикутників).
8. Знайти об’єднання множин вершин трикутників, вписаних у дане коло.(множина точок цього кола).
9. Задані множини A={p,r,s,t}, B={o,n,r,t,q}.
а) Назвати елементи, які належать множині А і множині В. Як називається множина, яка складається із таких елементів?
б) Назвати елементи, які належать множині А або множині В. Як називається множина, яка складається із таких елементів.
10. Відомо, що А ∩ В = С і х ∈ С. Чи правильно, що:
а) х ∈ А;
б) х ∈ В;
в) х ∉ А;
г) х ∉ В;
д) х ∈ А і х ∈ В;
е) х ∈ А і х ∉ В?
11. Відомо, що А ∪ В = С і х ∈ С. Чи можна стверджувати,що:
а) х ∈ А;
б) х ∈ В;
в) х ∉ В;
г) х ∉ В;
д) х ∈ А або х ∈ В;
е) х ∈ А і х ∈ В?
12. Записати елементи перетину і об’єднання множин А і В, якщо:
|
а) |
А={а,о,і,у,ю}, |
В={а,б,і,к,о}; |
|
б) |
А={3,6,9,!2,15}, |
В={6,1,2,5,9,13}; |
|
в) |
А={1,2,3,4,5,6}, |
В={12,34,56}; |
|
г) |
А={к,е,р,ю,в,л,м}, |
В={м,л,ю,в,е,к,р}; |
|
д) |
А={к,л,м,н}, |
В={і,к,л,м,н,о,п}. |
13. Відомо, що А – множина прямокутних трикутників, В – множина рівнобедрених трикутників. З’ясувати, які із висловлювань істинні:
а) Елементами множини А ∩ В є прямокутні рівнобедрені трикутники.
б) Множині А ∪ В прямокутні і рівнобедрені трикутники.
в) Множині А ∪ В належать прямокутні або рівнобедрені трикутники.
14. А - множина прямокутників, В – множина квадратів. Встановити, в якому відношенні знаходяться дані множини, зобразити їх за допомогою кругів Ейлера і серед висловлювань указати істинні:
а) А ∩ В – множина квадратів.
б) А ∩ В – множина прямокутників.
в) А ∪ В – множина квадратів.
г) А ∪ В – множина прямокутників.
15. Сформулюйте характеристичну властивість елементів перетину і об’єднання наступних множин:
а) К – множина дівчат у вашому класі, Р – множина учасників танцювального гуртка у вашому класі.
б) К – множина учнів восьмих класів школи, Р – множина відмінників школи.
в) К – множина натуральних чисел, кратних 4, Р – множина парних натуральних чисел.
16.Пояснити, про об’єднання яких множин йде мова в означенні:
а) променя; б)ламаної; в) многокутника.
17. А – множина білявок у класі, В – множина учнів класу, що сидять за першими партами. Сформулюйте умови, при яких:
а) А ∩ В = Ǿ;
б) А ∩ В ≠ Ǿ;
в) А ∩ В = В;
г) А ∩ В = А;
д) А ∪ В = Ǿ;
е) А ∪ В ≠ Ǿ;
є) А ∪ В = А;
ж) А ∪ В = В.
18. Сформулюйте характеристичну властивість елементів множини А В С і А ∪ В ∪ С, якщо А – множина чотирикутників, В – множина квадратів, С – множина паралелограмів. Побудувати круги Ейлера для даних множин.
19. Відомо, що А – множина парних натуральних чисел, В – множина двозначних натуральних чисел. З’ясувати, які висловлювання істинні:
а) Множині А ∩ В належать двозначні парні натуральні числа.
б) Множина А ∩ В складається із двозначних натуральних чисел.
в) Елементами множини А ∪ В є парні або двозначні натуральні числа.
г) Елементами множини А ∪ В є парні натуральні числа і непарні двозначні числа.
55. Знайти перетин і об’єднання множин:
а) N і Z; б) Z і Q; в) Q і N.
20. Діаграма, яка наведена на рисунку, зображує множини X, Y, M. Указати, яка з наступних множин зображена на заштрихованій частині діаграми:
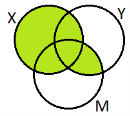 а) (X ∩ Y) ∪ M;
а) (X ∩ Y) ∪ M;
б) X ∪ (Y ∩ M);
в) X ∩ (Y ∪ M);
г) X ∩ Y ∩ M;
д) (X ∪ Y) ∩ М.
21. На рисунку за допомогою кругів Ейлера зображені множини І, А і В:
І – множина учнів восьмих класів школи,
А – множина учнів восьмих класів, які відвідують волейбольну секцію
В – множина учнів восьмих класів які відвідують біологічний гурток.
Яким множинам належать учні x, y, z, t? Які з даних висловлювань істинні?
а) Учень t не відвідує біологічний гурток. б) Учень t відвідує математичний гурток. в) Учень t не відвідує ні волейбольну секцію, ні біологічний гурток. 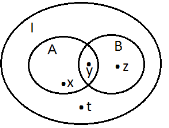
- СКІНЧЕННІ МНОЖИНИ
Множина натуральних чисел містить нескінченну кількість елементів, така множина називається нескінченною. Множина одноцифрових натуральних чисел містить 10 елементів, така множина називається скінченною, кількість елементів позначають N(A)=10.
Нехай А і В – такі скінченні множини, що ![]() тоді очевидно, що кількість елементів множин А і В дорівнює сумі N(A) і N(В):
тоді очевидно, що кількість елементів множин А і В дорівнює сумі N(A) і N(В):
N(A![]() ) = N(А)+N(В).
) = N(А)+N(В).
Наприклад, якщо ж множини А і В такі, що ![]() тоді до суми N(А)+N(В) двічі входить кількість елементів їх перетину, тоді формула для обчислення кількості елементів множини A
тоді до суми N(А)+N(В) двічі входить кількість елементів їх перетину, тоді формула для обчислення кількості елементів множини A![]() має вигляд:
має вигляд:
N(A![]() ) = N(А)+N(В) - N(A
) = N(А)+N(В) - N(A![]() ).
).
Наприклад, А-множина учнів класу, що відвідують математичний гурток N(A)=20, В-множина учнів класу, що відвідують фізичний гурток N(В)=13, кількість учнів, що полюбляють і математику і фізику - 6, тоді кількість учнів у класі, що відвідують гуртки дорівнює:
N(A![]() )=20+13 – 6 = 27.
)=20+13 – 6 = 27.
Вище згадана формула має місце для обчислення елементів множини А![]() В
В![]() С. Якщо А, В, С – скінченні множини та
С. Якщо А, В, С – скінченні множини та ![]() то
то
N(A![]() ) = N(А)+N(В)+N(С)- N(A
) = N(А)+N(В)+N(С)- N(A![]() )-N(В
)-N(В![]() )- N(A
)- N(A![]() ).
).
Якщо![]() тоді потрібно врахувати кількість спільних елементів всіх трьох множин N(A
тоді потрібно врахувати кількість спільних елементів всіх трьох множин N(A![]() С):
С):
N(A![]() ) = N(А)+N(В)+N(С)- N(A
) = N(А)+N(В)+N(С)- N(A![]() )-N(В
)-N(В![]() )- N(A
)- N(A![]() )+N(A
)+N(A![]() С).
С).
Наприклад, у 8 класі навчається 30 учнів, секцію баскетболу відвідують 15 учнів, волейбольну 10 учнів, 13 учнів полюбляють шахи. На баскетбол і волейбол ходять 17 учнів, волейбол і шахи – 5 учнів, на секцію шахів баскетбол – 2 учні. Скільки учнів займаються у всіх трьох секціях, якщо 4 учнів в класі не займаються спортом.
Кількість елементів множини N(A![]() )=30-4-26. Отримаємо рівняння 26=15+10+13-17-5-2+ N(A
)=30-4-26. Отримаємо рівняння 26=15+10+13-17-5-2+ N(A![]() С), звідки N(A
С), звідки N(A![]() С)=12.
С)=12.
Задачі для самостійного розв’язування.
1. З 38 учнів класу хор відвідують 28 учнів, а 17 спортивну секцію . Скільки спортсменів відвідують хор, якщо 4 учні не відвідують жодної секції?
2. У двох класах 50 учнів, всі вивчають іноземні мови. Англійську вивчають 30 учнів, німецьку – 21, французьку – 15 учнів. Англійську та німецьку мови вивчають 13 учнів, англійську та французьку – 10 учнів. Скільки учнів вивчають всі три мови?
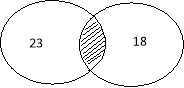 3. Знайдіть N(A
3. Знайдіть N(A![]() , якщо N(A
, якщо N(A![]() =9.
=9.
4. В школі 1400 учнів. З них 1250 уміють кататися на лижах, 952 – на ковзанах. Ні на лижах, ні на ковзанах не вміють кататися 60 учнів. Скільки учнів уміють кататися і на лижах і на ковзанах? (862 учні).
5. Нехай А - множина дільників числа 15;
В – множина простих чисел, менших 10;
С – множина парних чисел, менших 9.
Назвати елементи цих множин і знайти А ∪ В, А ∩ С, В ∩ С, (А ∪ С) ∩ В, А ∩ В ∩ С.
6. В групі із 100 туристів 70 чоловік знають англійську мову, 45 знають французьку мову і 23 чоловіки знають обидві мови. Скільки туристів в групі не знають ні англійської, ні французької мови? (8 туристів з групи).
7. А – підмножина множини натуральних чисел, кожний елемент множини А є число, кратне або 2, або3, або 5. Знайти кількість елементів в множині А, якщо серед них є:
70 чисел, кратних 2;
60 чисел, кратних 3;
80 чисел, кратних 5;
32 числа, кратних 6;
35 чисел, кратних 10;
38 чисел, кратних 15;
20 чисел, кратних 30.
(125 чисел)
8. В одному з відділів магазину звичайно купують або один торт, або одну коробку цукерок, або один торт і одну коробку цукерок. В один з днів було продано 57 тортів і 36 коробок цукерок. Скільки було покупців. Якщо 12 чоловік купили і торт і коробку цукерок? (81 чоловік)
9. В спортивному таборі 65% дітей вміють грати у футбол, 70% - у волейбол і 75% - у баскетбол. Яка найменша кількість дітей, які вміють грати і у футбол, і у волейбол, і у баскетбол? (10%)
10. Кожний з учнів класу у зимові канікули рівно два рази був у театрі, при цьому спектаклі А, В і С бачили відповідно 25, 12 і 23 учні. Скільки учнів в класі? Скільки з них бачили спектаклі А і В, А і С, В і С? (30; 7; 18; 5).
11. Протягом тижня у кінотеатрі демонстрували фільми А, В і С. З 40 школярів, кожний передивився або всі три фільми, або один з трьох, фільм А бачили 13, фільм В – 16, фільм С – 19. Знайти, скільки учнів переглянули всі три фільми? (4 учні).
12 З 40 учнів 30 уміють плавати, 27 уміють грати у шахи і тільки 5 не уміють ні того, ні іншого. Скільки дітей уміють плавати і грати у шахи? (22 учні).
13. На уроці літератури учитель вирішив дізнатись, хто із 40 учнів класу читав книжки А, В і С. Результати опитування такі:
книгу А читало 25 учнів
книгу В – 22 учні
книгу С – 22 учні
книгу А або В читали 33 учні
книгу А або С - 33 учні
книгу В або С – 31 учень
всі три книги прочитали 10 учнів.
Скільки учнів прочитали тільки по одній книзі? Скільки учнів не читали ні однієї з цих трьох книг? (тільки А – 6,тільки В – 5, тільки С – 4, не прочитали жодної книги – 3).
14. За допомогою кругів Ейлера розв’язати задачу.
Із 100 студентів 28 вивчають англійську мову, 30 – німецьку, 42 – французьку, 10 – англійську і французьку, 5 – німецьку і французьку, 3 – німецьку, англійську і французьку. Скільки студентів не вивчають жодної мови? Скільки студентів вивчають лише французьку, лише англійську, лише німецьку мови? ( жодної – 15, тільки німецьку – 25, тільки англійську – 18, тільки французьку – 30).
15. В одній множині 40 елементів, а в другій - 30. скільки елементів може бути в їх:
а) перетині;
б) об’єднанні?
16. Кожен учень в класі вивчає англійську або французьку мови. Англійську мову вивчає 25 чоловік, французьку – 27 чоловік, а англійську і французьку – 18 чоловік. Скільки учнів в класі?
17. На аркуші паперу накреслили круг площею 78 см2 і квадрат площею 55 см2. площа перетину круга і квадрата дорівнює 30 см2. Не зайнята кругом і квадратом частина аркуша має площу 150 см2. Знайти площу аркуша паперу.
18. В бригаді 25 робітників. Серед них 20 робітників молодші 30 років і 15 робітників старші 20 років. Чи може таке бути?
19. В дитячому садку 52 дитини. Кожний з них любить цукерки або морозиво. Половина дітей любить цукерки, а 20 чоловік – цукерки і морозиво. Скільки дітей любить морозиво?
- ЕКВІВАЛЕНТНІСТЬ ТА ПОТУЖНІСТЬ МНОЖИН
Дві множини називають еквівалентними (кількісно еквівалентними), якщо між ними можна встановити взаємно-однозначну відповідність. Іноді стверджують, що це множини з однаковою потужністю ![]() .
.
Множина ![]() , еквівалентна множині натуральних чисел N, називається зчисленною множиною. Властивість зчисленності передбачає, що кожному елементу множини можна поставити у відповідність натуральне число, тобто всі елементи множини можна занумерувати. При цьому:
, еквівалентна множині натуральних чисел N, називається зчисленною множиною. Властивість зчисленності передбачає, що кожному елементу множини можна поставити у відповідність натуральне число, тобто всі елементи множини можна занумерувати. При цьому:
а) будь-яка множина еквівалентна зчисленній множині є зчисленною множиною;
б) будь-які дві зчисленні множини є еквівалентними множинами;
в) будь-яка підмножина зчисленної множини є множиною зчисленною або скінченною;
г) довільне об'єднання скінченної та зчисленної множин є множиною зчисленною.
Поряд із цим, безконечну (нескінченну) множину, яка не є зчисленною, ми будемо називати незчисленною множиною. Множина всіх дійсних точок відрізка (0,1) є множиною потужності континуум. Всі множини, рівнопотужні з нею називатимемо множинами континуальної потужності. Доведено, що множина дійсних чисел є рівнопотужною із множиною всіх дійсних точок відрізка (0,1), а отже, множиною потужності континуум.
ДЕКАРТІВ ДОБУТОК МНОЖИН
Декартів добуток (прямий декартів добуток) множин X та Y - це множина усіх можливих впорядкований пар або кортежів, першими компонентами яких є елементи множини X, а другими - елементи множини Y.
Декартів добуток множин X та Y позначається як X × Y: X × Y = { (x, y) | x ∈ X ∧ y ∈ Y }
Тут впорядкована пара (x, y) елементів x, y є множина {{x}, {x, y}}, яка має таку властивість, що (x, y) ≠ (y, x).
Множена дійсних чисел-сукупність усіх раціональних та ірраціональних чисел.
Дійсні числа можна зображувати точками числової осію
Дійсні числа - це позитивні числа, негативні числа або нуль. Всі дійсні числа діляться на раціональні та ірраціональні. Перші - це числа, представлені у вигляді дробу. Другі - це дійсне число, що не є раціональним.
Приклади задач з розв’язанням
Приклад 1. Довести тотожність ![]() .
.
Доведення. Покажемо, що будь-який елемент із множини ![]() є одночасно елементом множини
є одночасно елементом множини ![]() . Для того, щоб
. Для того, щоб ![]() необхідно, щоб
необхідно, щоб ![]() . Аналогічно,
. Аналогічно, ![]() , якщо
, якщо ![]() . З іншого боку, якщо
. З іншого боку, якщо ![]() , то
, то ![]() . Отже, якщо
. Отже, якщо ![]() , то
, то ![]() , тобто
, тобто ![]() .
.
Покажемо тепер, що будь-який елемент із множини ![]() буде елементом множини
буде елементом множини ![]() . Нехай
. Нехай ![]() . Якщо
. Якщо ![]() , то
, то ![]() , якщо
, якщо ![]() , то
, то ![]() . Отже, якщо
. Отже, якщо ![]() , то
, то ![]() . З іншого боку, якщо
. З іншого боку, якщо ![]() , то
, то ![]() . Аналогічно, якщо
. Аналогічно, якщо ![]() , то
, то ![]() . Отже, якщо
. Отже, якщо ![]() , то
, то ![]() , а значить
, а значить ![]() . Враховуючи попередньо одержане:
. Враховуючи попередньо одержане: ![]() і
і ![]() , матимемо
, матимемо ![]() . Тотожність доведено.
. Тотожність доведено.
Дане завдання можна подати, використовуючи графічну інтерпретацію. Для цього необхідно показати, що область, якій належать елементи множини ![]() співпадає з областю, якій належать елементи множини
співпадає з областю, якій належать елементи множини ![]() , використовуючи діаграми Ейлера-Венна.
, використовуючи діаграми Ейлера-Венна.
Приклад 2. Задано множини ![]() :
:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Знайти результат виконання операцій над множинами
. Знайти результат виконання операцій над множинами ![]() .
.
Розв’язування. Виконуючи дане завдання, необхідно використати визначення операцій над множинами, а також деякі з відомих законів.
![]() ;
; ![]() ;
; ![]() ;
;
Тоді
![]()
Отже, обчислимо ![]() .
.
Приклад 3. Задано множини ![]() :
:
![]() ;
; ![]() ;
; ![]() R – множина дійсних чисел. Чи будуть рівнопотужними множини
R – множина дійсних чисел. Чи будуть рівнопотужними множини ![]() і
і ![]() ?
?
Розв’язування. Очевидно, що обидві задані множини є нескінченними. Визначимо потужність кожної із них. Оскільки множина ![]() містить всі парні числа, кратні 3, вона є підмножиною множини натуральних чисел, а отже, її потужність є зчисленною. Елементами множини
містить всі парні числа, кратні 3, вона є підмножиною множини натуральних чисел, а отже, її потужність є зчисленною. Елементами множини ![]() є всі дійсні числа за винятком натуральних парних чисел. Так як ця множина є підмножиною дійсних чисел, її потужність – континуум. Отже, множини
є всі дійсні числа за винятком натуральних парних чисел. Так як ця множина є підмножиною дійсних чисел, її потужність – континуум. Отже, множини ![]() та
та ![]() не є рівнопотужними.
не є рівнопотужними.
ОЛІМПІАДНІ ЗАДАЧІ
1. Знайдіть перетин множин М і Р, якщо М = {прості числа, менші від 40},
Р = {непарні числа, більші від 14}.
2. Знайдіть перетин, об'єднання і різницю множин K i L, якщо K = {1, 2, 3, 4, 5, 6, 7}, L = {2, 4, 6}.
Варіанти відповідей:
1. {1, 2, 3, 4, 5, 6, 7}
2. {2, 4, 6}
3. {1, 3, 5, 7}
4. порожня множина
5. {1, 2, 2, 3, 4, 4, 5, 6, 6, 7}
1.Вкажіть номер варіанту відповіді, що відповідає перетину множин K i L?_____
2.Вкажіть номер варіанту відповіді, що відповідає об'єднанню множин K i L?_______
3.Вкажіть номер варіанту відповіді, що відповідає різниці множин K i L?______
- ЧИСЛОВІ МНОЖИНИ (МНОЖИНА НАТУРАЛЬНИХ І ЦІЛИХ ЧИСЕЛ)
Множина – одне з основних понять математики, що не підлягає формальному означенню. Його використовують для опису сукупності предметів або об’єктів. При цьому передбачається, що предмети (об’єкти) даної сукупності можуть відрізнити один від одного і від предметів, що не входять у цю сукупність. Наприклад, можна говорити про множину всіх книг даної бібліотеки, множину всіх вершин даного многокутника, множину всіх натуральних чисел, множину всіх точок даної прямої. Книги даної бібліотеки, вершини даного многокутника, натуральні числа, точки даної прямої є елементами відповідних множин.
Окремі найважливіші множини мають загальноприйняті назви та позначення:
- множина точок площини — геометрична фігура;
- множина точок, яким притаманна певна властивість, — геометричне місце точок (ГМТ);
- множина значень аргументу функції f — область визначення функції f, яку позначають D (f);
- множина значень функції f — область значень функції f, яку позначають E (f);
- множина натуральних чисел, яку позначають буквою N;
- множина цілих чисел, яку позначають буквою Z;
- множина раціональних чисел, яку позначають буквою Q;
- множина дійсних чисел, яку позначають буквою R.
Множини N, Z, Q, R — приклади числових множин. Також прикладами числових множин є числові проміжки. Наприклад, проміжки [–3; 2], (5; +∞), (–∞; –4] є числовими множинами.
Як правило, множини позначають великими латинськими літерами: A, B, C, D тощо. Об’єкти, які складають множину, називають елементами цієї множини. Зазвичай елементи позначають малими латинськими літерами: a, b, c, d тощо. Якщо a належить множині A, то пишуть a ∈ A (читають: «a належить множині A»). Якщо b не належить множині A, то пишуть b ∉ A (читають: «b не належить множині A»).
Множина натуральних чисел, розташованих між числами 21 і 22 не містить жодного числа. Така множина називається порожньою множиною. Порожня множина позначається знаком ![]() .
.![]()
Множини можуть бути скінченними і нескінченними. Їх можна задавати переліком елементів, які записуються у фігурних дужках, якщо множина не впорядкована (так як іграшки у мішку Діда Мороза), або в круглих дужках, якщо множина впорядкована (кожен елемент має своє конкретне місце, як цукерки у коробці з заглибинами), або описом їх основної властивості (натуральні числа, які менші 100 і т.п.).
В шкільному курсі математики прийняті стандартні позначення числових множин: N - множина натуральних чисел, Z – множина цілих чисел, Q - множина раціональних чисел, R – множина дійсних чисел.
За допомогою кругів Ейлера можна зобразити входження числових множин одна в одну: ![]() , тобто множина натуральних чисел N міститься в множині чисел Z, яка в свою чергу є підмножиною множини раціональних чисел Q, яка так само включається в множину дійсних чисел R.
, тобто множина натуральних чисел N міститься в множині чисел Z, яка в свою чергу є підмножиною множини раціональних чисел Q, яка так само включається в множину дійсних чисел R.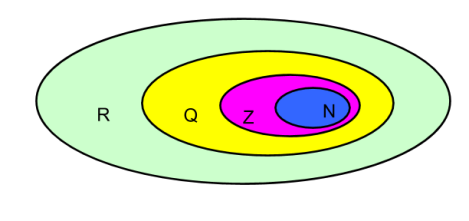
Означення. Множина називається числовою, якщо її елементами являються числа.
Означення. Множину натуральних чисел утворюють числа, використовувані для лічби:
1,2,3,4,5,6,7,....
Натуральні числа 1,2,3,… - це числа, що використовуються для рахування предметів або для вказування порядкового номера того чи іншого предмета серед однорідних предметів. Будь-яке натуральне число можна записати за допомогою десяти арабських цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Із двох натуральних чисел менше те, яке при підрахунку називають раніше. Наприклад, число 8 менше від 12 (записують так: 8 < 12). Коли одне число більше другого, це записують так: 386 > 99.
Найменше натуральне число – 1. Найбільшого натурального числа не існує.
 У III ст. до н. є. Архімед довів, що цей ряд чисел нескінченний. Множину натуральних чисел позначають літерою N. У цій множині введені дві дії: додавання та множення. Сума і добуток двох натуральних чисел є число натуральне. Наприклад, 5 + 6 =11, 2 • 5 = 10 і т. п. Різниця натуральних чисел не завжди є натуральним числом. Наприклад, 3 - 10 не є натуральним числом. Для того щоб можна було віднімати будь-які натуральні числа, вводяться Архімед число нуль та від'ємні числа.
У III ст. до н. є. Архімед довів, що цей ряд чисел нескінченний. Множину натуральних чисел позначають літерою N. У цій множині введені дві дії: додавання та множення. Сума і добуток двох натуральних чисел є число натуральне. Наприклад, 5 + 6 =11, 2 • 5 = 10 і т. п. Різниця натуральних чисел не завжди є натуральним числом. Наприклад, 3 - 10 не є натуральним числом. Для того щоб можна було віднімати будь-які натуральні числа, вводяться Архімед число нуль та від'ємні числа.
(287 до н. е. — 212 до н. е.)
Означення. Множину цілих чисел утворюють натуральні числа, число нуль та відʼємні числа.
Z - множина цілих чисел; ..., -3,-2, -1, 0, 1,2,3,4,5,6,7,...
Число нуль визначають як нейтральний елемент множини чисел. Це означає, що додавання цього числа до будь-яких інших чисел не змінює їх. Число нуль позначають 0. Отже,
а + 0 = а, де а — довільне число.
Цілим від'ємним числом - п, де п — натуральне число, називають таке число, для якого виконується тотожність:
(- п) + п = 0.
Число 0 не є натуральним числом. Натуральні числа, нуль та цілі від'ємні числа утворюють множину цілих чисел, яку позначають літерою Z.
Цілі числа можна зображати на прямій, узявши на ній за початок відліку точку О(0). Далі по обидва боки від точки О, якій відповідає 0, відкладають рівні відрізки, позначаючи їх кінці цифрами. Числа праворуч від 0 — додатні (зокрема, натуральні), ліворуч — від'ємні.
Таку пряму називають числовою прямою. Із двох чисел більшим вважається те, яке лежить далі праворуч на числовій прямій.
Приклади:
l) -3 • 5 = - 15;
2) 63:(-7) = -9.
2. Множення та ділення двох чисел з однаковими знаками:
-a • (-b) = a • b; - а : (-b) = a : b.
Приклади:
l) -3 • (- 10) = 3 • 10 = 30;
2) - 27 : (- 3) = 27 : 3 = 9.
3. Додавання двох чисел з однаковими знаками:
-a + (-b) = -(a + b).
Приклад:
-5 + (-6) = -(5 + 6) = -11.
4. Додавання двох чисел із різними знаками:
a>b=>-a + b= -(а - b); -а + b= b - а.
1) -5 + 10 = 5;
2) -17 + 3 = -14.
5. Віднімання двох чисел з однаковими знаками:
а>b => -а - (-b) = -(а - b); -a - (-b) =b - a.
1) -13 - (-8) = - (13 - 8) = -5;
2) -20 - (-45) = 45 - 20 = 25.
6. Віднімання двох чисел із різними знаками:
-а - b = -(а + b); a - (-b) = a + b.
Приклади:
1) -13 - 6 = -(13 + 6) = -19;
2) 40 - (-65) = 40 + 65 = 105.
Сума, різниця, добуток двох цілих чисел є ціле число. Проте частка двох цілих чисел не завжди є ціле число. Наприклад, частка 5 : 3 або -2 : 7 не є цілим числом. Щоб ділення цілих чисел виконувалося без обмежень, потрібно розширити поняття цілого числа, ввівши дробові числа. Q –множина раціональних чисел (звичайні дроби).
ПРИКЛАДИ ЗАДАЧ З РОЗВ’ЯЗАННЯМ
1. Іспит з математики склали 250 абітурієнтів, оцінку нижче п’яти балів отримали 180 чоловік, а витримали цей іспит 210 абітурієнтів (тобто не отримали «2»). Скільки чоловік отримали оцінки «3» і «4»?
Розв’язання. Нехай А – множина абітурієнтів, що витримали іспит, В – множина абітурієнтів, що отримали оцінку нижче п’яти балів, за умовою ![]() ,
, ![]() ,
, ![]() . Абітурієнти, що отримали оцінки «3» і «4», створюють множину
. Абітурієнти, що отримали оцінки «3» і «4», створюють множину ![]() . За формолою (1) знаходимо:
. За формолою (1) знаходимо:
![]()
2. Знайдіть найбільший спільний дільник чисел ![]() та
та ![]() .
.
Відповідь: ![]() .
.
Розв’язання. Перевіримо, що друге число діляться націло на ![]() . Дійсно:
. Дійсно:
![]() – ділиться на
– ділиться на ![]() . З властивостей НСД число
. З властивостей НСД число ![]() і є шуканим НСД.
і є шуканим НСД.
3. Знайдіть усі такі трицифрові числа, які при множенні на ![]() стають точним кубом натурального числа.
стають точним кубом натурального числа.
Відповідь: ![]() .
.
Розв’язання. Зрозуміло, що воно повинно ділитись на ![]() . Решта множників повинні бути кубами натуральних чисел. Випишемо послідовно ці куби та подивимось, чому дорівнює добуток цих чисел на
. Решта множників повинні бути кубами натуральних чисел. Випишемо послідовно ці куби та подивимось, чому дорівнює добуток цих чисел на ![]() .
.
![]() ,
, ![]() – двоцифрове число, умову не задовольняє.
– двоцифрове число, умову не задовольняє.
![]() ,
, ![]() – трицифрове число, умову задовольняє.
– трицифрове число, умову задовольняє.
![]() ,
, ![]() – чотирицифрове число, умову не задовольняє.
– чотирицифрове число, умову не задовольняє.
Зрозуміло, що більші числа тим паче умову не задовольняють.
4. Знайдіть різницю між сумою усіх парних чисел від 2 до 100 та сумою усіх непарних чисел від 1 до 99.
Відповідь: ![]() .
.
Розв’язання. Розіб’ємо усі числа на пари. ![]() , оскільки там усього 50 пар чисел.
, оскільки там усього 50 пар чисел.
5. Для яких цифр ![]() п’ятицифрові числа
п’ятицифрові числа ![]() та
та ![]() є послідовними натуральними числами.
є послідовними натуральними числами.
Відповідь: ![]() або
або ![]() .
.
Розв’язання. Якщо число закінчується не на ![]() , то при додаванні
, то при додаванні ![]() , змінюється лише остання цифра. Таким чином треба розглянути лише варіанти
, змінюється лише остання цифра. Таким чином треба розглянути лише варіанти ![]() або
або ![]() . Очевидно тоді, що також
. Очевидно тоді, що також ![]() та
та ![]() відповідно.
відповідно.
Якщо ![]() , то повинна виконуватись рівність:
, то повинна виконуватись рівність: ![]() , тоді четверта справа цифра числа, що у правій частині останньої рівності повинна бути
, тоді четверта справа цифра числа, що у правій частині останньої рівності повинна бути ![]() , тобто
, тобто ![]() і ми маємо таку рівність:
і ми маємо таку рівність:
![]() .
.
Якщо ![]() , то повинна виконуватись рівність:
, то повинна виконуватись рівність: ![]() , тоді четверта справа цифра числа, що у лівій частині останньої рівності повинна бути
, тоді четверта справа цифра числа, що у лівій частині останньої рівності повинна бути ![]() , тобто
, тобто ![]() і ми маємо таку рівність:
і ми маємо таку рівність:
![]() .
.
6. Задані 2013 чисел. Відомо, що сума будь-яких 11 з цих чисел – додатна. Чи обов’язково сума усіх 2013 чисел також додатна?
Відповідь: Обов’язково.
Розв’язання. Виберемо 11 найменших серед заданих чисел. Тоді їх сума – додатна. Але тоді усі інші числа – додатні. Бо якщо якесь з них, наприклад, ![]() , а серед обраних 11 числах усі не перевищують
, а серед обраних 11 числах усі не перевищують ![]() , то їх сума також недодатна. Таким чином одержали суперечність. Звідси висновок, сума найменших 11 чисел додатна. і усі інші числа також додатні. Тому сума усіх чисел – додатна.
, то їх сума також недодатна. Таким чином одержали суперечність. Звідси висновок, сума найменших 11 чисел додатна. і усі інші числа також додатні. Тому сума усіх чисел – додатна.
7. Знайдіть усі шестицифрові числа, які мають вигляд ![]() та діляться націло на 45.
та діляться націло на 45.
Відповідь: ![]() та
та ![]() .
.
Розв’язання. Зрозуміло, що ці числа повинні бути кратними 9 та 5. Розглянемо два випадки. Якщо воно закінчується на 0, тобто ![]() , то його сума цифр дорівнює
, то його сума цифр дорівнює ![]() . Тому для виконання умови повинно
. Тому для виконання умови повинно ![]() . Якщо воно
. Якщо воно ![]() , то його сума цифр дорівнює
, то його сума цифр дорівнює ![]() і повинно бути
і повинно бути ![]() . Таким чином маємо дві відповіді.
. Таким чином маємо дві відповіді.
8. Доведіть, що добуток трьох послідовних натуральних чисел, складений з другим із них, є кубом другого числа.
Розв’язання. Нехай друге число х. Тоді х - 1 х х + 1 + х = ( х² - х )( х+1 ) = х³+ х² - х² - х + х = х³.
9. У саду ростуть тільки сливи та груші. Кількість слив відноситься до кількості груш, як 3:8. Скільки слив у саду , якщо загальна кількість дерев більша за 130, але менша за 140?
Розв 'язання. Можна вважати, що слив Зх, а груш 8х. Якщо ![]()
![]() нескоротний дріб, де п >1, то одночасно п = 3 та п = 8, що не є можливим. Отже, х - натуральне число. Тоді 130 < 11х < 140, маємо, що 11х = 132, бо 132 єдине число від 130 до 140, яке націло ділиться на 11. Маємо остаточно, що слив - 36.
нескоротний дріб, де п >1, то одночасно п = 3 та п = 8, що не є можливим. Отже, х - натуральне число. Тоді 130 < 11х < 140, маємо, що 11х = 132, бо 132 єдине число від 130 до 140, яке націло ділиться на 11. Маємо остаточно, що слив - 36.
Відповідь: 36.
10. Число p – просте і р>3. Доведіть, що число р² –1 ділиться на 24.
Очевидно, (р-1)р(р+1) ділиться на 3, але р – просте число і р>3, не ділиться на 3, то (р-1)(р+1) ділиться на 3. Крім цього, р – непарне значить р-1 і р+1 – парні, тому одне із них ділиться на 2, друге – на 4, тобто (р-1)(р+1) ділиться на 8.
ОЛІМПІАДНІ ЗАДАЧІ
- Доведіть, що добуток трьох послідовних натуральних чисел, складений з другим із них, є кубом другого числа.
- У казковій країні живуть стоніжки і п’ятиголові дракони. Всього в них 31 голова і 665 ніг. У кожної стоніжки 1 голова. Скільки ніг у кожного дракона?.
- Якщо перемножити між собою перші 2017 простих чисел, тоді скількома нулями закінчуватиметься добуток?
- Знайдіть двоцифрове число, яке удвічі більше від зменшуваного на двійку числа, записаного тими ж цифрами, але у зворотному порядку.
- У натуральному числі переставили цифри й отримали число. Яке утричі менше від початкового. Доведіть, що початкове число ділиться на 27.
- Знайдіть два числа, якщо їх сума дорівнює 2283, а при діленні більшого з них на 7 у частці утворюється менше з чисел, а в остачі 5.
- Знайдіть суму всіх п’ятицифрових чисел, записаних за допомогою цифр 1, 4, 6, 7, 8 (цифри в числі не повторюються).
- На дошці написана послідовність чисел 3, 8, 15, 24, 35, ... За яким правилом утворені ці числа? Яке число стоїть на 92 місці?
- Доведіть, що з будь – яких ста цілих чисел завжди можна вибрати два таких числа, що їх різниця націло ділиться на 99.
- Якщо шукане двоцифрове число збільшити на 46, то утвориться число, добуток цифр якого дорівнює 6. Знайдіть це число за умови, що сума його цифр дорівнює 14.
- Знайти найменше натуральне число, яке починається цифрою 7 і зменшується у 5 разів, якщо переставити його першу цифру в кінець числа.
- Сума трьох тризначних чисел aab, aba, baa дорівнює 1998. Знайдіть усі трійки таких чисел.
- Дано 1999 чисел. Відомо, що сума будь – яких 99 з цих чисел додатна. Довести, що сума всіх чисел є додатна.
- Відомо, що для деяких простих чисел pq + pr =80 та pq + qr =425. Знайдіть суму p+q+r.
- Відомо, що M та N – два послідовних чотирицифрових числа. Яке найбільше значення може приймати різниця між сумами цифр чисел M та N.
- Про деяке двозначне число зроблені наступні твердження. «Це число або закінчується на 5, або ділиться на 7». «Це число або більше 20, або закінчується на 9». «Це число або ділиться на 12, або менше 21». Знайдіть всі двозначні числа, які задовольняють умовам задачі.
- Відомо, що до натурального числа n можна дописати справа будь-яку ненульову цифру c і одержане число буде ділитися на c. Знайдіть найменше значення, якого може набувати число n.
- Нехай S (n) позначає суму цифр десяткового запису натурального числа n. Чи існують натуральні числа k, l, m такі, що k + l + m / 3 – ціле число, і також S ( k + l ) < 150, S ( l + m ) < 150, S ( m + k ) < 150, S ( k + l +m )/3 > 2001?
- Натуральні числа m і n такі, що сума дробів (mn – 1)/(n-1) і ( nm – 1 )/(m – 1) є цілою. Довести, що кожен із даних дробів є цілим числом.
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ:
Бевз Г.П. Довідник з математики Посібник для учнів – Київ, «Радянська школа» 1981 – 262с.
Сарана О.А. Математичні олімпіади: просте і складне поруч Навчальний посібник – Київ, «Видавництво А.С.К.» – 2004 – 340с.
Валєєв К.Вища математика: Навчальний посібник: У 2-х частинах/ К.Г. Валєєв, І.А. Джалла-дова; М-во освіти і науки України, Київський нац. економічний ун-т . - К.: КНЕУ. – 2001. - Ч. 1. - 546 с.
Олімпіадні задачі з математики з розв’язками для учнів середньої школи.
Беседін Б.Б., Кадубовський О.А., Кадубовська В.М.,
Сьомкін В.С., Труш Н.І., Чуйко О.В. Олімпіадні задачі, розвʼязання задач II етапу Всеукраїнської олімпіади з математики – 2010. Випуск 8, навчальний посібник. Слов’янськ – 2011.
Михайло Підборочинський. Математична олімпіада, 8 клас. Сквира– 2009.
Галкин Е. В. Нестандартные задачи по математике. Задачи с целыми числами :[учебное пособие для учащихся 7-11 кл.] / Галкин Е. В. – Челябинск: Взгляд, 2005.– 271 с.
Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М : Просвещение, 1991. — С. 109-110.




ЧАСТИНА ІІ. ОСНОВИ ТЕОРІЇ ПОДІЛЬНОСТІ. МНОЖИНА ПРОСТИХ ЧИСЕЛ.
- ПОДІЛЬНІСТЬ НАЦІЛО ТА ЇЇ ВЛАСТИВОСТІ.
Вивчення основ теорії подільності у 8 класі дає ґрунтовну підготовку до розвя´язування задач олімпіадного характеру на подільність, пошук коренів рівняння в цілих числах, визначення остач від ділення та інших. Розглянуті твердження і методи є фундаментом теорії чисел і в той же ж самий час є найпростішими доступними учню прикладами теорем існування і єдності і прикладами найпростіших алгоритмів без чого немислимо створити правильне уявлення про математичну науку.
 Питання подільності натуральних чисел розглядалися уже в античні часи. Евкліду належить один з найвідоміших результатів математики, твердження, що не існує найбільшого простого числа, тобто множина простих чисел — нескінченна. Він також навів найперший в історії алгоритм, а саме алгоритм Евкліда, знаходження найбільшого спільного дільника двох натуральних чисел. Цікаво відзначити, що це — не тільки найдавніший, а й один з найефективніших алгоритмів в математиці, який майже не був вдосконалений за більш ніж дві тисячі років, що минули по тому.
Питання подільності натуральних чисел розглядалися уже в античні часи. Евкліду належить один з найвідоміших результатів математики, твердження, що не існує найбільшого простого числа, тобто множина простих чисел — нескінченна. Він також навів найперший в історії алгоритм, а саме алгоритм Евкліда, знаходження найбільшого спільного дільника двох натуральних чисел. Цікаво відзначити, що це — не тільки найдавніший, а й один з найефективніших алгоритмів в математиці, який майже не був вдосконалений за більш ніж дві тисячі років, що минули по тому.
Евклід
(325 г. до н. э.- 265 г. до н. э)
 Свій внесок у розвиток теорії подільності вніс німецький математик Карл Фрідріх Гаусс запровадивши поняття конгруенції за модулем, довів основну теорему арифметики. Проблемою пошуку універсальної формули для задання простих чисел займався відомий французький математик, юрист П´єр Ферма. Він висловив припущення, що всі числа виду
Свій внесок у розвиток теорії подільності вніс німецький математик Карл Фрідріх Гаусс запровадивши поняття конгруенції за модулем, довів основну теорему арифметики. Проблемою пошуку універсальної формули для задання простих чисел займався відомий французький математик, юрист П´єр Ферма. Він висловив припущення, що всі числа виду ![]() +1 є простими, n – ціле, невід´ємне, проте відомий математик Ейлер у XVIII ст. спростував це твердження.
+1 є простими, n – ціле, невід´ємне, проте відомий математик Ейлер у XVIII ст. спростував це твердження.
Карл Фрідріх Гаус
(1777-1855)
У курсі «Алгебри і теорії чисел» вищих навчальних закладів вивчається розділ про подільність цілих чисел. Всі теореми, означення для легшого вигляду теорії сформульовано для цілих додатних натуральних чисел і переносяться на цілі від’ємні числа. Всі теореми доводяться, але деякі доведення громіздкі і вимагають багато часу і місця для їх відтворення. Тому у курсі алгебри середньої школи, використовують багато тверджень зі спрощеним доведенням.
Говорять, що ціле число а ділиться на ціле число b, b≠0, якщо існує таке ціле число q, що а= b q.
Властивості подільності:
-
Якщо а≠0, то а
 а.
а.
-
Якщо а≠0, то 0
 а.
а.
-
Якщо а
 b то ka
b то ka  .
.
-
Якщо а
 b і b
b і b c, то a
c, то a 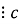 .
.
-
Якщо а
 m і b
m і b n, то ab
n, то ab 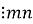 .
.
-
Якщо а
 c і b
c і b c, то (a±b)
c, то (a±b) 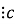 .
.
З властивостей подільності випливає спосіб розв´язування рівнянь в цілих числах.
Наприклад, розв´яжіть у цілих числах рівняння х2-4xy+3y2=3.
Намагаємося розкласти ліву частину рівняння на множники: х2-4xy+4y2- y2=3; (x-2y)2-y2=3; (x-3y)(x-y)=3, тоді рівняння рівносильне системі рівнянь:
![]()
![]()
Відповідь: (4; 1), (0; -1), (-4; -1), (0; 1).
Чи існує таке трицифрове число ![]() , що значення виразу
, що значення виразу ![]() +
+![]() +
+![]() є квадратом натурального числа?
є квадратом натурального числа?
Подамо вираз ![]() +
+![]() +
+![]() у вигляді суми розрядних одиниць:
у вигляді суми розрядних одиниць:
![]() +
+![]() +
+![]() =100a+10b+c+100b+10c+a+100c+10a+b=111(a+b+c)=
=100a+10b+c+100b+10c+a+100c+10a+b=111(a+b+c)=
=37·3(a+b+c). Оскільки сума одноцифрових чисел a+b+c≤27, тоді вираз не є квадратом натурального числа.
Задачі для самостійного розв’язування.
Розв´яжіть в цілих числах рівняння:
- x2+xy-6y2=6;
- xy=x+y;
- 2y2-xy-x2=2.
Трицифрове число ![]() кратне числу 37. Доведіть, що сума чисел
кратне числу 37. Доведіть, що сума чисел![]() +
+![]() також кратна числу 37.
також кратна числу 37.
2. ДІЛЕННЯ З ОСТАЧЕЮ. КОНГРУЕНЦІЇ ТА ЇХ ВЛАСТИВОСТІ
Ділення одного натурального числа на інше ціле не завжди виконується. Тому розглядають більш загальну дію — ділення з остачею.
Поділити натуральне число a на натуральне число b з остачею — означає подати число a у вигляді a=b·q+r, де a∊Z, b∊N. Число q при цьому називається неповною часткою, якщо остача не дорівнює нулю, а число r — остачею від ділення a на b. Наприклад, при діленні числа 27 на 6 неповна частка дорівнює 4, а остача – 3. Щоб знайти ділене при діленні з остачею, потрібно неповну частку помножити на дільник і до здобутого добутку додати остачу. Ділення з остачею завжди виконується, про що свідчить наведена теорема (теорема про ділення з остачею).
Теорема Нехай a∊Z, b∊N, тоді існують цілі числа q і r такі, що a=bq+r, де 0 ≤ r < b.
Цими вимогами q і r визначаються однозначно.
Наприклад, знайдіть остачу від ділення числа m на 6, якщо при діленні числа m на 18 остача дорівнює 11.
Подамо число m у вигляді m=18q+11, m=18q+6+5=6(3q+1)+5=6q1+5. Таким чином остача від ділення числа m на 6 дорівнює 5.
Поняття «конгруентності» чисел широко використовується в задачах на пошук остачі від ділення та доведенні кратності.
Цілі числа a і b називаються конгруентними за модулем m (m![]() , якщо остачі при діленні їх на число m рівні: a
, якщо остачі при діленні їх на число m рівні: a![]() .
.
Наприклад, 5![]() , тому що 5=2·2+1 та 3=2·1+1.
, тому що 5=2·2+1 та 3=2·1+1.
56![]() , 10
, 10![]() .
.
При розв´язуванні задач на пошук остач при ділення числа a на b доречно, використовуючи властивості конгруенцій, підібрати конгруенцію виду a![]() .
.
Приклад 1: знайдіть остачу від ділення 20122013 на 3. Розглянемо конгруенцію 2012![]() , тоді 20122013
, тоді 20122013![]() , 20122013
, 20122013![]() . Отже, остача від ділення дорівнює 2.
. Отже, остача від ділення дорівнює 2.
Приклад 2: остача від ділення трицифрового числа n=![]() на деяке одноцифрове число дорівнює 8, знайдіть число n.
на деяке одноцифрове число дорівнює 8, знайдіть число n.
Оскільки остача від ділення 8, тоді розглянемо конгруенцію за модулем 9: n![]() , тоді 2·100+10b+b
, тоді 2·100+10b+b![]() ,
,
200+11b![]() ,
,
11b![]() ,
,
11b![]() ,
,
11b![]() ,
,
11b![]() ,
,
b![]() .
.
Отже, шукане число b=![]() , n=233.
, n=233.
Приклад 3: доведіть, що 15n + 23n – 30 кратне 7.
Оскільки 15![]() , 23
, 23![]() ,тоді 15n + 23n
,тоді 15n + 23n![]() ,
,
15n + 23n![]() , 15n + 23n
, 15n + 23n![]() .
.
Задачі для самостійного розв’язування.
- Відновіть запис:
34![]() , 4
, 4![]() , -1
, -1![]() ,
,
![]() , -2
, -2![]() , *
, *![]() .
.
- Знайдіть остачу від ділення 292013 на 4; 52014 на 3.
-
Остача від ділення трицифрового числа n=
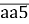 на деяке одноцифрове число дорівнює 8, знайдіть число n.
на деяке одноцифрове число дорівнює 8, знайдіть число n.
- Доведіть, що 62n + 3n+2 +3n кратне 11.
3. НАЙБІЛЬШИЙ СПІЛЬНИЙ ДІЛЬНИК, НАЙМЕНШЕ СПІЛЬНЕ КРАТНЕ ДВОХ НАТУРАЛЬНИХ ЧИСЕЛ
Найбільшим спільним дільником (НСД) декількох чисел називають найбільше число, на яке кожне з даних чисел ділиться без остачі.
У 6 класі учні знайомляться з способом знаходження НСД(m; n) за допомогою розкладання даних чисел на прості множники. Цей спосіб достатньо простий, легкий і зручний. Але він має суттєвий недолік: якщо дані числа великі, та ще й не дуже легко розкладаються на множники, то знайти НСД стає досить складною. До того ж, доволі попрацювавши, ми можемо дістати, що НСД(m; n)=1, і тоді вся робота виконана марно, тобто числа m і n – взаємно прості. Евклід знайшов чудовий спосіб знаходження НСД без попереднього опрацювання чисел. Цей спосіб називають алгоритмом Евкліда. Щоб знайти НСД двох натуральних чисел, треба спочатку більше число розділити на менше, потім менше число ділимо на остачу від ділення, а потім остачу від першого ділення ділимо на остачу від ділення другого і т.д. Остання в цьому процесі остача, яка не дорівнює нулю, і буде НСД даних чисел.
Наприклад, знайдемо НСД (102;84). Розглянемо ланцюжок рівностей:
НСД (102;84)= НСД (84;18)= НСД (18;12)= НСД (12;6)= НСД (6;0)=6.
Найменше спільне кратне НСК двох цілих чисел a, b називаємо найменше натуральне число, яке є кратним обох цих чисел. Позначаємо НСК(a, b). Отже НСК (a, b) є найменшим натуральним числом, яке ділиться без залишку на обидва числа a, b. Є різні способи знаходження спільного кратного кількох чисел. У 6 класі дається такий спосіб: Для знаходження спільного кратного двох чисел треба: 1) розкласти дані числа на прості множники; 2) доповнити розклад одного з них тими множниками розкладу другого числа, яких немає в розкладі першого; 3) обчислити добуток знайдених множників.
Розглянемо інший спосіб знаходження НСК(a, b), застосувавши теорему, що НСК (a, b)· НСД (a, b)= a · b.
Приклад: знайдіть НСК (a, b) та НСД (a, b), якщо а=1260, b=270. Знайдемо НСД (1260, 270)= НСД (990, 270)= НСД (270, 180)= НСД (180, 90)= =НСД (180, 90)=90.
НСК (1260, 270)· НСД (270, 180)= 1260· 270;
НСК (1260, 270) = 1260 · 270/90=1260·3=3780.
4. ПРОСТІ І СКЛАДЕНІ ЧИСЛА
Запроваджуючи поняття «просте число», «складене число», потрібно звертати увагу на те, щоб учні правильно формулювали означення і в разі наявності помилки у сформульованому означенні відразу наводили контр приклад. Практика свідчить, що в означені простого числа деякі учні забувають слово «лише» і формулюють означення так: натуральне число називають простим, якщо воно має два різних дільники. Контрприклад: число 6 має два різких дільники 2 і З, але не є простим.
Натуральне число р називається простим, якщо воно має лише два різних натуральних дільника: одиницю і р.
Натуральне число, яке має більш ніж два натуральних дільники, називають складеним.
Варто зауважити, що число 1 не є ні простим числом, ні складеним.
Теорема Евкліда. Не існує найбільшого натурального простого числа (множина простих чисел нескінченна).
Основна теорема арифметики, теорема К. Гаусса. Будь-яке натуральне число, більше одиниці, або є простим, або може бути представлене у вигляді добутку простих чисел і таке представлення є єдиним з точністю до порядку множників.
Мала терема Ферма. Якщо натуральне число а не ділиться націло на просте число р, то ар-1![]() 1 (
1 (![]() .
.
Для розв´язування задач зручно використовувати
наслідок з теореми. Для будь-якого натурального числа а і простого р виконується ар ![]() (
(![]() .
.
Наприклад, довести, що 4247+4742 є складеним числом. Оскільки число 43 просте і 42<43<47, розглянемо конгруенції, використовуючи малу теорему Ферма:
4243 ![]() (
(![]() та 4743
та 4743 ![]() (
(![]()
4247 ![]() (
(![]() та 4742
та 4742 ![]() (
(![]()
![]() (
(![]() ).
).
Додамо почленно конгруенції ![]() + 4742
+ 4742 ![]() (
(![]() . Отже, значення виразу 4247+4742 кратне 43, є складеним.
. Отже, значення виразу 4247+4742 кратне 43, є складеним.
Щоб знайти найбільший спільний дільник двох чисел, є спосіб, відомий під назвою алгоритму Евкліда, або способу послідовного ділення.
Алгоритм Евкліда, або алгоритм послідовного ділення, полягає ось у чому. Нехай дано натуральні числа a і b, a > b.
Поділимо перше число на друге, дістанемо остачу r1 (r1 < b). Тепер b поділимо на r1, дістанемо остачу r2 (r2 < r1), далі поділимо r1 на r2 і т. д.
Оскільки після кожного наступного кроку утворюється остача, менша від попередньої, то через скінченну кількість кроків дістанемо остачу, яка дорівнює нулю: ділення відбудеться націло і процес припиниться.
Остання відмінна від нуля остача rk, на яку націло ділиться остача rk-1, буде найбільшим спільним дільником чисел a і b.
Справді, запишемо сказане як ланцюжок рівностей:
a = bq + r1,
b = r1q1 + r2,
r1 = r2q2 + r3,
...
rk-2 = rk-1qk-1 + rk,
rk-1 = rkqk.
З останньої рівності випливає, що rk є дільником rk-1, rk = (rk; rk-1). З передостанньої рівності випливає, що rk ділить також rk-2 і rk = (rk-1; rk-2).
Так, послідовно піднімаючись кроками вгору, дістанемо, що rk = (a; b).
Приклад. Знайти НСД чисел 9765 і 6944.
 Розв'язання.
Розв'язання.
9765 = 6944 · 1 + 2821,
6944 = 2821 · 2 + 1302,
2821 = 1302 · 2 + 217,
1302 = 217 · 6.
Відповідь. 217.
- ОЗНАКИ ПОДІЛЬНОСТІ ЧИСЕЛ
Ознака подільності — алгоритм, що дозволяє порівняно швидко визначити, чи є число кратним заздалегідь заданому.
Ознаки подільності чисел
|
Дільник |
Умова подільності |
Приклади |
|
1 |
Число 1 є дільником будь-якого натурального числа. |
6,4789,78019 |
|
Остання цифра є парною |
1294: 4 є парне. |
|
|
Сума цифр повинна ділитися на 3. |
405: 4 + 0 + 5 = 9. 9 ділиться на 3. |
|
|
Якщо число, утворене двома останніми цифрами ділиться на 4. |
2092: 92 ділиться на 4. |
|
|
Остання цифра або 5 або 0. |
490: остання цифра 0. 325: остання цифра 5. |
|
|
Якщо число ділиться на 2 і на 3. |
24: число ділиться на 2 і на 3. |
|
|
7 |
Число розбивається на блоки по три цифри, починаючи з кінця. Число ділиться на 7, якщо різниця суми блоків, що стоять на парних місцях, і суми блоків, що стоять на непарних місцях, ділиться на 7. |
2911272: 911 — (2 + 272) = 637. 637 ділиться на 7. |
|
Якщо сума подвоєного числа без останніх двох цифр і останніх двох цифр ділиться на 7. |
364: (3·2) + 64 = 70. 70 ділиться на 7. |
|
|
Якщо сума числа без останньої цифри і останньої цифри, помноженої на 5, ділиться на 7 |
364: 36 + (5·4) = 56. 56 ділиться на 7. |
|
|
Різниця між числом без останньої цифри і подвоєної останньої цифри повинна ділитись на 7. |
364: 36 − (2·4) = 28. 28 ділиться на 7. |
|
|
Якщо число, утворене останніми трьома цифрами, ділиться на 8. |
5128: 128 ділиться на 8. |
|
|
Якщо число сотень є парне, то число, утворене двома останніми цифрами повинне ділитись на 8. |
624: 6 — парне, 24 ділиться на 8. |
|
|
Якщо число сотень є непарним, то до числа, утвореного двома останніми цифрами, потрібно додати 4. Таке число повинне ділитись на 8. |
352: 52+4 = 56. 56 ділиться на 8. |
|
|
Сума цифр повинна ділитися на 9. |
2880: 2 + 8 + 8 + 0 = 18. 18 ділиться на 9. |
|
|
Остання цифра 0. |
130: остання цифра 0. |
|
|
Число розбивається на блоки по дві цифри, починаючи з кінця. Сума блоків повинна ділитись на 11. |
627: 6 + 27 = 33. 33 ділиться на 11. |
|
|
Якщо різниця між числом без останньої цифри і останньою цифрою ділиться на 11. |
627: 62 — 7 = 55. 55 ділиться на 11. |
|
|
Якщо сума цифр, що стоять на парних місцях відрізняється від суми цифр, що стоять на непарних місцях, починаючи з кінця, на число, що кратне 11. |
182919: (9 + 9 + 8) — (1 + 2 + 1) = 22. |
|
|
Якщо число ділиться на 3 і на 4. |
324: воно ділиться і на 3, і на 4. |
|
|
Число без останньої цифри множать на два і віднімають останню цифру. Таке число повинне ділитись на 12. |
324: (32x2) − 4 = 60. 60 ділиться на 12. |
|
|
Число ділиться на блоки по три цифри, починаючи з кінця. Сумуються блоки, що стоять на парних і непарних місцях. Різниця цих сум повинна ділитись на 13. |
2911272: 911 — (2 + 272) = 637. 637 ділиться на 13. |
|
|
До числа без останньої цифри додають останню цифру, помножену на 4. Утворене число повинне ділитись на 13. |
338: 33 + (8·4) = 65. 65 ділиться на 13. |
|
|
Від числа без останньої цифри віднімають останню цифру, помножену на 9. Утворене число повинне ділитись на 13. |
637: 63 − (7·9) = 0. 0 ділиться на 13. |
|
|
Якщо число тисяч є непарним, то до числа, утвореного останніми трьома цифрами, додають 8. |
3408: 408+8 = 416. 416 ділиться на 16. |
|
|
Число без останніх двох цифр множать на 4 і додають число, утворене останніми двома цифрами. Результат повинен ділитись на 16. |
176: (1·4) + 76 = 80. 80 ділиться на 16. |
|
|
Якщо число, складене з двох останніх цифр, ділиться на 25. |
134250: 50 ділиться на 25. |
|
|
Число ділять на блоки по три цифри, починаючи з кінця. Число, утворені блоками сумують. Сума повинна ділитись на 37. |
2651272: 2 + 651 + 272 = 925. 925 ділиться на 37. |
|
|
Від числа без останньої цифри віднімають останню цифру, помножену на 11. Результат повинен ділитися на 37. |
925: 92 − (5x11) = 37. |
Приклади розв’язування задач
Задача 1. Доведіть, що 420 -1 ділиться на 5.
Доведення
Будь-який парний степінь числа 4 закінчується на 6, тому 420 закінчується на 6, тоді 420 -1 закінчується на 5, тому (420 -1) ⋮ 5.
Задача 2. Доведіть, що 960 +5 ділиться на 2.
Доведення
Будь-який степінь числа 9 закінчується на непарні числа 1 або 9. Якщо до цього числа додати непарне число 5, то отримане число буде парним, отже, (960 +5) ⋮ 2
Задача 3. Найменше спільне кратне двох чисел, які не діляться одне на одне, дорівнює 630, а їх найбільший спільний дільник дорівнює 18. Знайти ці числа.
Розв’язання
Нехай x і y – шукані числа. Тоді за умовою мають місце рівності
НСК(x, y) = 630 = 2·32·5 ·7 (1)
НСД (x, y) =18 =2·32 (2)
З (2) випливає, що шукані числа мають вид
x =18 ·x ', y = 18 ⋅y ', де x' і y ' – взаємнопрості числа.
З (1) випливає два можливі випадки:
1) x = 18⋅5, y = 18⋅ 7 (або ж x = 18 ⋅7 y = 18⋅5) ;
2) x = 18⋅5⋅ 7, y = 18⋅1 (або ж x = 18 ⋅1 y = 18⋅5⋅7) ;
Оскільки шукані числа не діляться одне на одне, то розв’язки, що відповідають другому випадку, не задовольняють умову задачі. Тому шуканими числами є числа 90 і 126.
Задача 4. Доведіть, що значення виразу 967 - 225 - 486 є кратним 10.
Доведення
Очевидно, що остання цифра натурального степеня багатоцифрового числа співпадає з останньою цифрою відповідного степеня числа, що задається останньою його цифрою. Тоді отримуємо:
967 закінчується цифрою 6, 225 – цифрою 2, а 486 – цифрою 4. Звідси випливає, що задане число закінчується цифрою 0, а отже воно ділиться на 10.
Задача 5. Сума трьох цілих чисел ділиться на 6. Довести, що й сума кубів цих чисел ділиться на 6.
Доведення
Подамо вираз x3+y3+z3 у наступному вигляді
x3+y3+z3=x3+y3+z3-(x+y+z)+(x+y+z)==(x3-x)+(y3-y)+(z3-z)+ (x+y+z)==x(x2-1)+x(x2-1)+ z(z2-1)+(x+y+z)== (x-1)x(x+1)+(y-1)y(y+1)+(z-1)z(z+1)+(x+y+z).
Звідки:
x3+y3+z3=(x-1)x(x+1)+(y-1)y(y+1)+(z-1)z(z+1)++(x+y+z) (1)
Зауважимо, що з трьох послідовних чисел одне завжди ділиться на три, і принаймні одне ділиться на два. Тому добуток трьох послідовних цілих чисел завжди ділиться на шість.
Отже, кожен з перших трьох доданків правої частини рівності (1) ділиться на шість. За умовою останній доданок – вираз (x+y+z) – також ділиться на шість. І тому права частина рівності (1), а разом із нею і ліва.
Задача 6. Знайдіть серед чисел виду 1+3n три числа, кратні 5.
Розв’язання
Для того, щоб число виду 1+3n ділилося на 5, необхідно, щоб остання цифра в записі цього числа була 0 або 5.
Нехай ці числа закінчуються 0, тоді числа виду 3n повинні закінчуватися на 9 і ділитися на 3.
Розглянемо деякі з них, що задовольняють першу вимогу: 9,19,29,39,40,59,69,…
Виберемо з них ті, що задовольняють і другу вимогу: 9,39,69,…
Отже, серед чисел виду 1+3n на 5 діляться числа: 9+1= 10, 39 +1= 40, 69 + 1 =70
ЗАДАЧІ ДЛЯ ОЛІМПІАД
Задача 1. Доведіть, що 1716 +9 ділиться на 10.
Доведення
Степінь числа 17 закінчується на:
1-й – 7; 2-й – 9; 3-й – 3; 4-й – 1; 5-й – 7; …; 16-й – 1. Якщо до числа, що закінчується 1 додати 9, то число буде закінчуватися на 0 і буде ділитися на 10.
Задача 2. Доведіть, що 810 - 108 ділиться на 8.
Доведення
810-108=810-(2∙5)8=810-28∙58=81+9-23+5∙58=8∙89-23∙25∙58=
=8∙89-8∙25∙58=8∙(89-25∙58)⋮8
Задача 3. Доведіть, що квадрати натуральних чисел при діленні на 3 можуть
давати лише остачі 0 та 1.
Доведення
Число п при діленні на 3 може давати остачі 0, 1, 2.
Якщо п = 3k, то п2 = (3k )2= 9k2 ділиться на 3.
Якщо п = 3k + 1, то п2 = (3k+1)2 = 9k2 + 6k + 1 дає в остачі 1.
Якщо п = 3k + 2, то п2 =(3k+2)2 = 9k2 + 12k + 4 дає в остачі 1.
Задача 4. Довести, що значення виразу ![]() ділиться на 19 при будь-якому натуральному n.
ділиться на 19 при будь-якому натуральному n.
Доведення
Застосуємо метод математичної індукції.
Доведення методом математичної індукції проводиться за таким алгоритмом:
1) перевірити правильність твердження Т(1);
2) припустити, що правильним є твердження Т(k), k ![]() 1;
1;
3) довести, використовуючи це припущення, що правильним буде твердження Т(k+1);
4) зробити висновок, що за принципом математичної індукції твердження Т(n) правильне для будь-якого n![]() N.
N.
Якщо n = 1, то ![]() .
.
Припустимо, що для деякого натурального k (k ≥ 1) значення виразу ![]() ділиться на 19. Доведемо, що значення виразу
ділиться на 19. Доведемо, що значення виразу![]() також ділиться на 19.
також ділиться на 19.
Дійсно, 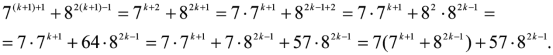 Зважаючи на те, що
Зважаючи на те, що ![]() і
і ![]() , то і вся сума буде ділитися
, то і вся сума буде ділитися
на 19, а отже, ![]() ділиться на 19 при будь-якому натуральному n.
ділиться на 19 при будь-якому натуральному n.
Задача 5. Натуральні числа а і b – взаємнопрості. Довести, що НСД (a+b, a2+b2) дорівнює 1 або 2.
Доведення
Припустимо, що числа a+b, a2+b2 діляться на с.
Тоді число 2ab = (a+b)2 – (a2+b2) також ділиться на d, тому 2a2 = 2b(a+b) - 2ab також ділиться на d.
За умовою числа а і b – взаємно прості, тому числа a2, b2 також взаємно прості.
Отже d =1або d=2.
Задача 6. Доведіть, що n3 + 2n ділиться на 3 при будь-якому натуральному п.
Доведення
Число п при діленні на 3 дає одну з трьох остач: 0, 1, 2. Тому можливі три випадки: п = 3k, п = 3k + 1, п = 3k + 2.
У першому випадку п3 і 2п діляться на 3, а тому і п3+2п також ділиться на 3.
У другому випадку п3 дає остачу 1, 2п — остачу 2, а 1+2 ділиться на 3.
У третьому випадку п3 дає остачу 2, 2п — остачу 1, а 2+1 ділиться на 3.
Задача 7. Знайдіть найменше натуральне число, сума остач від ділення якого на 5 та 7 дорівнює 9.
Розв’язання
Остача від ділення на 5 не більша за 4, а остача від ділення на 7 не більша за 6. Тому сума цих остач може дорівнювати 9 лише у двох випадках: коли число дає остачу 4 при діленні на 5 та остачу 5 при діленні на 7 або дає остачу 3 при діленні на 5 та остачу 6 при діленні на 7.
Остачу 4 при діленні на 5 дають числа 9,14,19,…, серед них остача 5 при діленні на 7 вперше зустрічається у числа 19. Аналогічно остачу 3 при діленні на 5 дають числа 8,13,18,…, серед них остача 6 при діленні на 7 вперше зустрічається у числа 13.
Відповідь: 13.
Задача 8. Знайти всі числа k такі, що 2∙36n + k∙23n+1-1 при всіх натуральних n ділиться на 7.
Розв’язання
36n при діленні на 7 дає таку саму остачу, що й 23n, тобто 1.
Тому число 2∙36n + k∙23n+1-1 ділиться на 7 тоді і тільки тоді, коли ділиться на 7 число 2 + 2k – 1 = 2k + 1. Яким же повинно бути k, щоб число 2k + 1ділилося на 7?
Для цього треба, щоб 2k при діленні на 7 давало в остачі 6. А це буде тоді, коли число k при діленні на 7 дає в остачі 3.
Отже, 2∙36n + k∙23n+1-1 при всіх натуральних n ділитиметься на 7 тоді і тільки тоді, коли k = 7m +3, де m – будь-яке ціле число.
Задача 9. Довести, що коли m>2 (m ∈N), то сума всіх натуральних чисел, менших від m і взаємно простих з m (у тому числі й 1), кратна m.
Доведення
Нехай k – довільне натуральне число, яке взаємно просте з m і менше, ніж m.
Тоді числа m – k і m також взаємно прості, оскільки в противному разі існувало б таке натуральне число n ≠ 1 при якому одночасно виконуватимуться рівності:
m – k = np (1)
m = nq (2)
Де p і q – деякі натуральні числа. З цих рівностей випливає, що
k = n(q-p), а це, якщо взяти до уваги рівність (2), суперечить тому, числа m і k - взаємно прості.
Таким чином, кожному натуральному k , меншому від m і взаємно простому з ним, відповідає число m – k, яке також взаємно просте з m, причому різним k відповідають різні числа m – k.
Отже, всі числа, менші від m і взаємнопрості з ним можна розбити на пари
(k; m-k), серед яких немає рівних, бо m>2.
Оскільки сума чисел кожної пари дорівнює m, то сума чисел усіх таких пар, тобто всіх чисел, менших від m і взаємнопростих з m, кратна m, а отже, ділиться на m, що й треба було довести.
Задача 10. Знайти всі двоцифрові числа n, для яких
НСК(4n,1000000) = 4НСК(n,1000000)
Розв’язання
Розглянемо, на який степінь числа 2 діляться ліва та права частини рівності з умови. Оскільки 1000000 ділиться на 26, то 4НСК(n,1000000) ділиться принаймні на 28. Тому НСК(4n,1000000) теж має ділитися на 28.
Але тоді хоча б одне з чисел 4n та 1000000 ділиться на 28. Отже 4n ділиться на 28, а n ділиться на 26 = 64. Оскільки n – двоцифрове число, то звідси n=64.
Відповідь: n = 64
Задача 11.Запис деякого 2013-значного числа складається лише з цифр 5 та 8. Довести, що можна викреслити з нього одну цифру так, аби дiстати число, яке дiлиться на 11.
Доведення
Доведемо твердження задачi для (2k + 1)-значних чисел iндукцiєю за k ≥ 1. При k = 1 маємо тризначне число, яке мiстить принаймнi двi однаковi цифри. Тому можна викреслити одну цифру так, щоб залишилося число 55 або 88. Нехай тепер твердження доведено для (2k + 1)-значних чисел при всiх 1 ≤ k < n.
Доведемо його для k = n. Добре вiдомо, що число дiлиться на 11 тодi й лише тодi, коли рiзниця мiж сумами цифр на парних та на непарних мiсцях дiлиться на 11. Таким чином, викреслювання з числа двох сусiднiх однакових цифр не впливає на подiльнiсть 2 на 11. Тому якщо в (2n + 1)-значному числi є двi сусiднi однаковi цифри, то з нього можна викреслити цi двi цифри та отримати (2n−1)-значне число, з нього викреслити ще одну цифру так, аби дiстати число, яке дiлиться на 11, а потiм вiдновити викресленi цифри.
Залишилось довести твердження лише для двох (2n + 1)-значних чисел, у записi яких цифри 5 та 8 чергуються. З цих чисел достатньо викреслити середню цифру, адже пiсля цього суми цифр на парних та непарних мiсцях очевидно стануть рiвними.
Задача 12. Знайти всі цілі додатні n, для яких число 2n-1 ділиться на 7.
Розв’язання
Нехай n кратне трьом. Тоді n можна представити у вигляді n=3k і
2n-1=23k-1=8k-1.
Але різниця степенів з однаковими показниками ділиться на різницю основ, тобто 8k-1 ділиться на 8 – 1 = 7. Тому 2n-1 ділиться на 7 при n кратному трьом.
Якщо n не кратне трьом, то n=3k+1 або n=3k+2.
У випадку n=3k+1 маємо 2n-1=23k+1-1=2(8)k-1=2(7+1)k-1, але (7+1)k при діленні на 7 дає в остачі 1, 2(7+1)k при діленні на 7 дає в остачі 2. Отже, при діленні
2n-1= 2(7+1)k-1 на 7 отримуємо в остачі 1, при n=3k+1 число 2n-1 не ділиться на 7.
У випадку n=3k+2 маємо 2n-1=23k+3-1=4(7+1)k-1 при діленні на 7 отримуємо в остачі 3.
Отже, 2n-1 ділиться на 7 тоді і тільки тоді, коли n кратне трьом.
Задачі для самостійного розв’язування.
- Знайдіть НСД (72;108), НСД (210;294).
- Встановіть чи є числа 154 і 165 та 14332 і 8156 взаємно простими.
- Знайдіть натуральні числа a і b, якщо НСД (а; b)=7, НСК (а; b)=1001.
- Дерев'яний брусок завдовжки 48 см, завширшки 30 см і заввишки 24 см потрібно розрізати без відходів на найменшу кількість рівних кубів. Скільки кубів одержимо?
- ПРОСТІ ТА ВЗАЄМНО ПРОСТІ ЧИСЛА. ВЛАСТИВОСТІ ПРОСТИХ ЧИСЕЛ.
Означення. Простими числами називаються натуральні числа більші за 1, які мають рівно два дільники: 1 і саме це число.Числа, що мають більше двох дільників, називаються складеними.
Означення. Два числа, що не мають спільних дільників крім 1, називаються взаємно простими.
ВЛАСТИВОСТІ ВЗАЄМНО ПРОСТИХ ЧИСЕЛ
1) Цілі числа a та b взаємно прості тоді і тільки тоді, коли існують цілі числа u та v такі, що au+bv=1.
Доведення. Необхідність випливає з Т3.
Достатність. Нехай d є спільним дільником чисел a та b. Тоді ліва частина рівності au+bv=1 ділиться на d, а отже і права частина 1 також ділиться на d, отже ![]() .
.
2) Якщо добуток ab натуральних чисел ділиться на натуральне число m, і a взаємно просте з m, то b ділиться на m.
Доведення. ![]() , отже існують цілі u,v такі, що
, отже існують цілі u,v такі, що ![]() . Помноживши останню рівність на b, одержимо
. Помноживши останню рівність на b, одержимо ![]() . Ліва частина ділиться на m, отже і b
. Ліва частина ділиться на m, отже і b
ділиться на m.
3) Якщо натуральні числа a і b взаємно прості, і c ділиться на a і на b, то воно ділиться і на їх добуток ab.
Доведення. Дійсно, ![]() ділиться на b, D(a,b)=1, отже за властивістю 2, с ділиться на b
ділиться на b, D(a,b)=1, отже за властивістю 2, с ділиться на b
З властивості 3) випливають ознаки подільності на числа, які є добутками двох взаємно простих чисел.
4) Якщо цілі числа ![]() такі, що кожне число
такі, що кожне число ![]() взаємно просте з кожним числом
взаємно просте з кожним числом ![]() то їх добутки
то їх добутки ![]() взаємно прості.
взаємно прості.
Наслідок: Якщо цілі числа a i b взаємно прості, то при натуральних k і m числа ![]() та
та ![]() теж взаємно прості.
теж взаємно прості.
Наведені твердження дуже прості і здаються майже тривіальними. Проте з них можна вивести деякі не зовсім тривіальні речі, наприклад, що
5) Степінь з натуральним показником дробового раціонального додатного числа не може бути цілим числом.
6) Якщо ціле додатнє число c не є m–им степенем цілого числа (при натуральному m), то воно не є m–им степенем дробового раціонального числа. Тому ![]() є або цілим числом, або ірраціональним.
є або цілим числом, або ірраціональним.
Надалі через p,q будемо позначати прості числа.
1. Якщо просте число p ділиться на деяке натуральне число n не рівне 1, то воно співпадає з n.
2. Для кожного натурального числа a і простого p, або a ділиться на p, або a і p взаємно прості.
3. Якщо просте число q ділиться на просте p, то ці числа співпадають.
4. Якщо добуток чисел a і b ділиться на просте число p, то хоча б одне з них ділиться на p.
Ця властивість може бути узагальнена на будь-яку кількість співмножників.
5. Кожне натуральне число більше за 1 має хоча б один простий дільник.
6. Найменший простий дільник складеного числа a не первищує a.
7. Теорема 4. (Основна теорема арифметики) Будь-яке натуральне число більше за 1 розкладається в добуток простих натуральних чисел, і цей добуток є єдиним з точністю до порядку множників.
Доведення.1) існування розкладу доведем методом математичної індукції по n. Якщо число n – просте, то ми можемо вважати, що воно подано у вигляді добутку простих, і зрозуміло, що таке подання єдине. Якщо n- складене, то воно має простий дільник p, n=pm, де ![]() , і за припущення індукції, m розкладається в добуток простих.
, і за припущення індукції, m розкладається в добуток простих.
2) Єдиність. Тут ми доведемо її індукцією за кількістю k простих множників в розкладі.
Припустимо, що розклад всіх натуральних чисел, в яких кількість простих множників не перевищує k, є єдиним (з точністю до порядку множників). Доведемо це для будь-якого елемента ![]() , який може бути розкладеним на k+1 простих множників. Нехай
, який може бути розкладеним на k+1 простих множників. Нехай
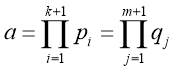 - два розклади числа a, де
- два розклади числа a, де ![]() . За властивістю П4, хоча б один зі співмножників
. За властивістю П4, хоча б один зі співмножників ![]() ділиться на
ділиться на ![]() . Не втрачаючи загальності ( бо це питання нумерації) вважаємо, що
. Не втрачаючи загальності ( бо це питання нумерації) вважаємо, що ![]() . Оскількі
. Оскількі ![]() - просте , то за властивістю П3
- просте , то за властивістю П3 ![]() .
.
![]() , де
, де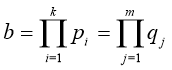 . В першому добутку стоїть k співмножників, отже за припущенням індукції
. В першому добутку стоїть k співмножників, отже за припущенням індукції ![]() і оба розклади відрізняються тільки порядком простих елементів. Теорему доведено.
і оба розклади відрізняються тільки порядком простих елементів. Теорему доведено.
8. Теорема 5 (теорема Евкліда) Множина всіх простих чисел нескінчена.
Дов. Припустимо, що існує скінчена кількість простих чисел ![]() . Легко бачити, що число
. Легко бачити, що число ![]() взаємно просте з будь-яким
взаємно просте з будь-яким ![]() , але за Т4 воно має ділитися принаймні на одне з
, але за Т4 воно має ділитися принаймні на одне з ![]() Одержане протиріччя доводить теорему.
Одержане протиріччя доводить теорему.
Задачі
1. (жарт) Якщо вiд задуманого тризначного числа
вiдняти 7, то воно роздiлиться на 7,
вiдняти 8, то воно роздiлиться на 8,
вiдняти 9, то воно роздiлиться на 9.
Яке число задумано?
2. Звертаючись до продавця магазину, покупець сказав:
Порахуйте, будь-ласка, за двi пачки солi - по 45 коп.,
за 2 шматки мила - по 1грн 50 коп., за три пачки цукру та за 6
коробок сiрникiв, але вартiсть пачки цукру та коробки сiрникiв
я не пам`ятаю.
Касир видав покупцю чек на 9 грн 17 коп. Подивившись на чек,
покупець повернув його та сказав:
- Ви помилились в пiдрахунку загальної суми.
Яким чином покупець знайшов помилку?
3. Чи змiниться при дiленнi з остачею частка та остача, якщо дiлене
та дiльник збiльшити в n разiв? Вiдповiдь пiдтвердити прикладом.
4. (майже жарт) Знайти найменше серед всiх тих чисел, якi
при дiленнi на 2 дають в остачi 1,
при дiленнi на 3 дають в остачi 2,
при дiленнi на 4 дають в остачi 3,
при дiленнi на 5 дають в остачi 4,
при дiленнi на 6 дають в остачi 5,
при дiленнi на 7 дають в остачi 6,
при дiленнi на 8 дають в остачi 7.
5. (так само) Чи може бути таке число, яке
при дiленнi на 3 дає в остачi 1,
при дiленнi на 4 дає в остачi 2,
при дiленнi на 5 дає в остачi 3,
при дiленнi на 6 дає в остачi 4.
6. Дано три послiдовних натуральних числа, з яких
перше - парне. Довести, що добуток цих чисел дiлиться на 24.
7. Число p2- 1 (p > 3 - просте число) дiлиться на 24 :
8. Довести, що добуток 5 послiдовних натуральних чисел дiлиться на 120.
9. Натуральне число при дiленнi на 11 має остачу 4. Довести,
що його квадрат при дiленнi на 11 має остачу 5.
10. Натуральне число при дiленнi на 5 має остачу 4. Довести,
що сума куба цього числа та його квадрату дiлиться на 5.
11. Натуральне число при дiленнi на 5 має остачу 1, а друге
число при дiленнi на 5 має остачу 2. Довести, що сума квадратiв
цих чисел дiлиться на 5.
12. Довести, що 1111+1212+1313 дiлиться на 10.
13. Довести, що 3 n+2 -2n+2 +3n -2n дiлиться на 10 при будь-якому натуральному n.
14. Довести, що 116+146-1363 дiлиться на 10.
15. Довести, що сума кубiв трьох послiдовних натуральних чисел
дiлиться на 9.
16. Чи може в натуральному рядi чисел стояти пiдряд 10 складених чiсел?
- РОЗКЛАДАННЯ НА МНОЖНИКИ
У загальному вигляді задача розкладання на множники многочленів, вже не кажучи про більш складні вирази, засобами шкільної математики нерозв'язна. Але в тих найпростіших випадках, які зустрічаються в шкільній і практиці, досить тих методів, які вивчаються в 7 класі (винесення спільного множника за дужки, застосування тотожностей скороченого множення, метод групування).
Розглянемо, як слід використовувати ці методи для розв’язання задач розкладання на множники різних виразів.
Розкладання на множники многочленів виконується за допомогою наступних операцій в такому порядку:
1. Винесення спільного множника за дужки. Перевірити, чи не мають всі одночлени, з яких складається многочлен, спільного множника. Якщо так, то винести його за дужки, якщо немає, то перейти до наступної операції.
2. Застосування тотожностей скороченого множення. Перевірити, чи не містить заданий многочлен такий вираз, до якого безпосередньо можна застосувати одне з тотожностей скороченого множення (різницю квадратів, квадрат чи куб двочлена, різниця або сума кубів). Якщо так, то застосувати цю тотожність, якщо немає, то перейти до наступної операції.
3. Групування членів. Розбити многочлен на кілька (дві або більш) груп і до кожної з них спробувати застосувати перші дві операції.
Якщо жоден з розглянутих методів не дав можливості розв’язати рівняння, то є універсальний, не досить легкий, метод невизначених коефіцієнтів.
Суть цього методу полягає в тому, що вигляд множників – многочленів, на які розкладається вираз, заздалегідь відомий. Цей метод спирається на такі твердження: 1) два многочлени тотожно рівні тоді й тільки тоді, коли рівні їхні коефіцієнти при однакових степенях ; 2) будь-який многочлен третього степеня розкладається на добуток двох многочленів: многочлена першого та многочлена другого степенів; 3) будь-який многочлен четвертого степеня розкладається на добуток двох многочленів другого степеня.
Розглянемо суть способу невизначених коефіцієнтів на задачах:
1. Нехай треба розкласти на множники: х3-3х2+4х-2
Будемо шукати многочлени a3 x3 + a2 x2 + a1 x + a0, і x − a такі, щоб виконувалась тотожність: х3-3х2+4х-2=(x − a)(x2 + bx + c)
Розкривши дужки в правій частині цієї тотожності та звівши подібні члени,
отримаємо: (x − a)(x2 + bx + c) =х3+bx2+cx-ax2-bax-ac=x3+(bx2-ax2)+(cx-bax)-ac= =x3+x2(b-a)+x(c-ab)-ac, де a, b, c – дiйснi числа; причому a – дiйсний ноль многочлена х3-3х2+4х-2.
Два многочлени одного степеня тотожно рівні тоді i тільки тоді, коли рівними є їх вiдповiднi коефіцієнти. Тому одержуємо систему рівнянь для знаходження a, b, c, тобто введених невизначених коефіцієнтів, які вважаються цілими числами:
{b-a=-3, c-ab=4, -ac=-2; ⇔ {b=a-3, c=a(a-3)+4, ac=2.
Оскільки a і c – цілі числа, то знайдемо всі можливі пари цих чисел з рівності : ac=2:
- а=±2, с=±1;
- а=±1, с=±2;
Єдина пара, що задовольняє систему: а=1, с=2.
Розв’язуючи далі систему в цілих числах, отримаємо: а=1, b=-2, с=2.
Остаточно маємо: х3-3х2+4х-2=(х-1)(х2-2х+2)
2.Розкладемо на множники: х4+х3-7х2+2х+4
Подамо вираз у вигляді добутку двох квадратних тричленів із цілими
коефіцієнтами:
х4+х3-7х2+2х+4=(x2+ax+b)(x2+cx+d)
Розкриємо дужки, зведемо подібні доданки і винесемо спільний множник за дужки:
(x2+ax+b)(x2+cx+d)=x4+(a+c)x3+(ac+b+d)x2+(ad+bc)x+bd
Прирівняємо коефіцієнти при однакових степенях у даному і останньому рівняннях:
{a+c=1, ac+b+d=-7, ad+bc=2 і bd=4.
Із рівності bd=4 маємо такі можливі пари чисел:
b=±1 d=±4
b=±4 d=±1
b=±2 d=±2
Підставивши дані пари чисел в систему, знаходимо коефіцієнти a і c.
Маємо:a=-1, b=-1, c=2, d=-4.
Остаточно маємо: х3-3х2+4х-2=(х2-х-1)(х2+2х-4).
ПРИКЛАДИ ЗАДАЧ З РОЗВ’ЯЗАННЯМ .
Завдання 1. Розкласти на множники многочлен
6х3у+3х2у2—3ху3.
Застосуємо послідовність операцій до заданого многочлену.
Всі члени многочлена мають спільний множник 3х. Виносимо його за дужки. Маємо: 6х3у+3х2у2—3ху3=3ху (2х2+ху—у2).
Тепер спробуємо розкласти на множники многочлен , що стоїть в дужках. Очевидно, що до нього перші дві операції (винесення спільного множника за дужки і застосування тотожностей скороченого множення) незастосовні. Спробуємо тоді згрупувати члени. Так як многочлен можна розбити мінімум на два многочлени і в кожному з них повинно бути не менше двох членів, то, для того щоб можна було зробити групування, в многочлені має бути не менше чотирьох членів. А в даному многочлені мається всього три. В такому випадку розіб'ємо один з членів на два. Зручніше це зробити з першим членом. Тоді многочлен матиме такий вигляд:
2х2+ху—у2= х2 + х2+ху—у2
Згрупувати його члени можливо таким чином:
х2 + х2+ху—у2= (х2—у2) + (х2+ху).
Бачимо, що перша група членів є різницею квадратів і, отже, до неї може бути застосована відповідна тотожність, а до другої групи може бути застосована операція винесення спільного множника х за дужки:
(х2—у2) + (х2+ху)=(х—у) (х+у)+х (х + у).
Розглядаючи тепер отримані два добутки, бачимо, що вони містять спільний множник (х + у). Виносимо його за дужки:
(х—у)(х+у)+х(х + у) =(х + у) (х—у+х) = (х + у) (2х—у).
Тоді остаточно отримаємо:
6 х3у + 3 х2у2 — 3 ху3= 3х (х + у) (2х—у).
Завдання 2. Розкласти на множники многочлен : x 3 + 2x2 − 3
I спосiб (метод групування)
x 3+2x2−3=x3– x2 +3x2−3=x2 (x−1)+3(x2−1) = x2 (x−1)+3(x −1)(x +1)= (x−1)(x2 +3x+3).
II спосiб (метод групування)
x3 +2x2−3 =x3 −1+2x2 −2 =x3−1+2(x2 −1) =(x −1)(x2 +x+1)+2(x −1)(x+1)=(x−1)(x2+x + +1+2x+2)=(x −1)(x2+3x+3).
III спосiб (метод «невизначених коефіцієнтів»)
Оскiльки рiвняння третього степеня ( a3 x3+a2 x2+a1x+a0 = 0 ) завжди має принаймнi один дiйсний корiнь, то многочлен третього степеня f(x)=a3x3+a2 x2 +a1 x + a0, зокрема даний, завжди має хоча б один дiйсний «ноль» (тобто таке значення x0 змiнної x, при якому f(x0) = 0 ). I тому даний многочлен третього степеня можна подати у виглядi:
x 3 + 2x2 − 3= (x − a)(x2 + bx + c) = x3 + x2 (b − a) + x(c − ab) − ac, де a, b, c – дiйснi числа; причому a – дiйсний ноль многочлена x 3 + 2x2 − 3. Прирівняємо коефіцієнти при однакових степенях x у лівій і правій частинах останньої рівності. Має мiсце система рiвнянь з трьома змiнними a, b, c
{b-a=2 c-ab=0 -ac=-3. ⇔{a-b=-2 ab=c ac=3. (1)
Не важко перевірити, що трійка a = 1; b = 3; c = 3 є розв’язком системи. Таким чином
x 3 + 2x2 − 3 = (x − a)(x 2 + bx + c) = (x − 1)(x 2 + 3x + 3).
Вiдповiдь: x 3 + 2x2 − 3 = (x − 1)(x2 + 3x + 3).
Завдання 3. Розкласти на множники вираз (у—z)3+(z — х)3+(х—у)3
I спосiб (метод групування)
Можна спочатку заданий вираз перетворити в многочлен стандартного вигляду, а вже потім спробувати розкласти його на множники.
Застосовуючи тотожність (куб двочлена) і зведення подібних членів, отримаємо:
(у—z)3+(z—х)3+(х—у)3=у3—3у2z+3уz2—z3+z3—3z2х+3zх2—х3+х3—3х2у+ +3ху2—у3=3(—zу2+уz2—z2х+х2z—х2у+ ху2).
Згрупуємо члени многочлена, що стоїть в дужках і застосуємо до цих груп операції винесення спільного множника за дужки і тотожність різниці квадратів:
3 ((—у2z+уz2) + ( — z2х+ху2) + (zх2—х2у)) == 3 (уz (z—у) —х (z2—у2) +х2 (z—у)) =
= 3 (уz (z—у) —х (z—у) (z+у) +х2 (z—у)).
Виносимо за дужки спільний множник (z—у):
(z—у) (уz—х (z+у) +х2) = 3 (z—у) (уz—хz—ху+х2)
У многочлені, що стоїть в других дужках, згрупуємо члени, а потім застосуємо операцію винесення спільного множника за дужки:
3(z—у) ((уz-хz)-(ху—х2))=3(z—у)(z (у—х)—х (у—х))=3(z—у)(у—х)(z—х).
II спосiб (метод групування)
Можна не перетворювати даний вираз до вигляду многочлена, а застосувати відразу операції з розкладання на множники. В даному випадку перші два доданки можна розкласти як суму кубів виразів(у —z) и (z—х):
(у—z)3+(z — х)3+(х—у)3=((у — z)+(z—х))((у—z)2—(у—z)(z—х)+(z—х)2)+(х—у)3= =(у—х) ((у—z)2—(у—z) (z—х) + (z—х)2)+(х—у)3
Бачимо, що в першому доданку є множник (у—х), а в другому (х— у). Тоді, змінивши знак другого доданка, винесемо за загальні дужки (у—х):
(у—х) ((у—z)2—(у—z)(z—х)+(z—х)2)+(х—у)3=(у—x)((y—z)2—(y—z)(z—x)+
+(z—x)2—(y—x)2)
У виразі, що стоїть в других дужках, згрупуємо члени по два по порядку і в першій групі винесемо за дужки (у—z), до другої групи застосуємо тотожність різниці квадратів:
(у—x)((y—z)2— (y—z)(z—x)+(z—x)2—(y—x)2)= (у—x)((y — z)(y—z—z+x)+ +(z—x—y+x)(z—x+y—x))= (у—x)((y—z)(y—2z+x)+(z—y)(z—2x+y)).
Змінимо знак першого доданка, для того щоб отримати спільний множник (z—у), який винесемо за загальні дужки:
(у—x)((y—z)(y—2z+x)+(z—y)(z—2x+y))= (у—x)((z—y)(—y+2z—x+z—2x+y))= =(у—x)(z—y) (3z—3x) = 3(у—x)(z—y) (z—x).
Остаточно маємо: (у—z)3+(z—х)3+(х—у)3=3(у—х)(z—y)(z—x).
Завдання 4. Розкласти на множники: (аb+ас+bс)(а+b+с)-аbс
(аb+ас+bс)(а+b+с)-аbс=a2(b+c)+ab(b+c)+ac(b+c)+bc(b+c)=
=(b+c)[a(a+b)+c(a+b)]=(b+c)(a+b)(a+c)
Завдання 5. Розкласти на множники: (a+b+с)3-a3-b3-c3 (a+b+с)3-a3-b3-c3=(a+b)3+3(a+b)2c+3(a+b)c2+c3-(a3+b3)-с3=
=(a+b) (a2+2ab+b2+3ac+3bc+3c2-a2+ab-b2) =(a+b)(3ab+3ac+3bc+3c2)= =3(a+b)[a(b+c)+с(b+c)]=3(a+b)(b+c)(a+c).
Завдання 6. Розкласти на множники: x5+x4+x3+x2+x+1
x5+x4+x3+x2+x+1=x(x4+x2+1)+ (x4+x2+1)= (x+1)(x4+x2+1)= (x+1)(x4+2x2+1-x2)= =(x+1)[(x2+1)2-x2]=(x+1)(x2+x+1)(x2-x+1).
Завдання 7 . Розкласти вираз аb-ba на два множники,один з яких дорівнює ab+ba.
Другий множник можна отримати, знайшовши частку від ділення заданого виразу на відомий множник:
(аb-ba):(ab+ba)=a2-b2ab:a2+b2ab=a2-b2a2+b2
Остаточно маємо: аb-ba=(ab+ba)a2-b2a2+b2 .
Завдання 7. Розкласти на множники: x10+x5+1
x10+x5+1=(x10+x9+x8)-(x9+8+x7)+(x7+x6+x5)-(x6+x5+x4)+(x5+x4+x3)-(x3+x2+x)+(x2+x+1)= x8(x2+x+1)-x7(x2+x+1)+ x5(x2+x+1)-x4(x2+x+1)+ +x3(x2+x+1)-x(x2+x+1)+ (x2+x+1)= (x2+x+1)(x8-x7+x5-x4+x3-x+1).
Завдання 8. Розкласти на множники: х8+х7+1
х8+х7+1=х8+х7+х6 –х6 –х5 –х4+х5+х4+х3 –х3 –х2– х+х2+х+1=
=х6 (х2+х+1)–х4 (х2+х+1)+х3(х2+х+1)–х(х2+х+1)+х2+х+1=
=(х2+х+1)(х6 –х4+х3–х+1).
При розв’язанні олімпіадних задач доводиться стикатися з нестандартними завданнями. Розглянемо деякі випадки необхідності розкладання виразів на множники.
Приклад 1. Розв’язати рівняння![]()
Скористаємося методом «невизначених коефіцієнтів». Подамо многочлен лівої частини рівняння у вигляді добутку двох квадратних тричленів, перемножимо їх та згрупуємо по степенях при змінних:
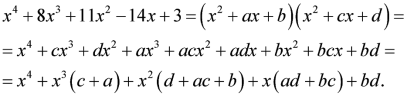
Порівняємо коефіцієнти при однакових степенях, складемо систему і розв’яжемо її 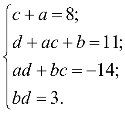
Шукаємо розв’язки в цілих числах, тому b може приймати значення ![]()
Якщоb=1, то d=3, тоді 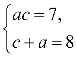 звідки
звідки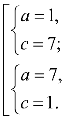
Але ці значення не задовольняють ІІІ рівняння системи.
Якщо b=3, то d=1, тоді 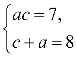 звідки
звідки 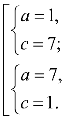
Ці значення також не задовольняють ІІІ рівняння системи.
Якщо b=-1, то d=-3, тоді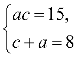 звідки
звідки 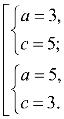
ІІІ рівняння системи задовольняє перша пара, отже![]()
![]()
![]()
![]()
![]()
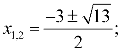
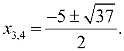
Відповідь: 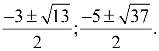
Завдання для самостійної роботи.
Приклад 1 Доведіть, що число n4+4 є складеним.
n4+4=(n4+4n2+4)-4n2=(n2+2)2 -(2n)2 =( n2+2- 2n)( n2+2+2n).
Приклад 2. Доведіть, що число 2006·2007·2008·2009+1 є точним квадратом.
Позначимо 2006 через n, тоді n(n+1)(n+2)(n+3)+1=(n2+3n)(n2+3n+2)+1=
=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2 , що й треба було довести.
Приклад 3. Довести, що многочлен х95+х94+…+х2+х+1 ділиться на многочлен (х31+х30 +…+х2+х+1)
х95+х94+…+х2+х+1=(1+х+…+х31)+х32(1+х+…+х31)+х64(1+х+…+х31)=
=(1+х+…+х31)(1+х32+х64).
Розкласти на множники:
Приклад 4. х3+5х2+3х-9
Відповідь: (х-1)(х+3)2
Приклад 5. х8+х+1.
Відповідь: (х2+х+1)(х6–х5+х3–х2+1).
Приклад 6 х4+х2+2х+2
Вказівка: Виділити та розкласти двочлен:
х4+1=х4+2х2+1-2х2=(х2+1)2-2х2=(х2+2х+1)(х2-2х+1)
Відповідь: (х2+2х+1) (х2-2х+1)
Приклад 7 a3+b3+c3+3abc
Відповідь:(a+b+c)(a2+b2+c2-ab-ac-bc)
Розв’язати рівняння:
Приклад 8 ![]()
Відповідь: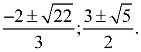
Приклад 9. ![]()
Відповідь: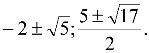
Приклад 10. ![]()
Відповідь: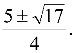
Приклад 11. ![]()
Відповідь: 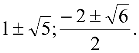
Приклад 12. ![]()
Відповідь: 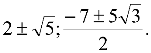
- ЛІНІЙНІ ДІОФАНТОВІ РІВНЯННЯ
Серед лінійних рівнянь примітне і почесне місце займають рівняння з цілими коефіцієнтами, для яких необхідно відшукати цілі розв’язки. Такі рівняння (і не тільки лінійні) зазвичай називають діофантовими на честь давньогрецького математика Діофанта. Такими рівняннями (а якщо точніше – то задачами, що зводяться до рішення діофантових рівнянь) цікавились не тільки в стародавній Греції, а і в Китаї, Індії,середньовічній Європі. В сучасній практиці також можуть зустрітись ситуації, що зводяться до рішення лінійних діофантових рівнянь.
Розглянемо детальніше лінійні діофантові рівняння з двома невідомими, тобто рівняння виду
ах +bу = с, (1)
якщо а, b, с – цілі числа (а ≠ 0, b ≠ 0 , с ≠ 0) для яких необхідно відшукати цілі розв’язки, тобто пари чисел (x;y) з цілими x і y. Такі рівняння можуть мати розв’язки, а можуть і не мати. Так, рівняння 6x+9y=8 не має цілих розв’язків, бо при будь-яких цілих x і y ліва частина ділиться на 3, а права – число 8 – не ділиться.
В загальному випадку, якщо d=НСД(а, b) і c не ділиться на d, то рівняння (1) розв’язку не має. Якщо ж і с ділиться на d, тобто а=а1d, b=b1d, c=c1d, то скоротивши обидві частини (1) на d, отримаємо рівняння з цілими коефіцієнтами
а1х +b1у = с1,
рівносильне даному. В зв’язку з цим можна вважати, що в рівнянні (1) НСД(а, b)=1.
Найпростіше розв’язувати діофантові рівняння х+bу = с (ах +у = с). Адже достатньо взяти любе ціле значення у, позначимо його через у0, і тоді х0= с –bу0 разом з у0 створюють пару цілих чисел, що є розв’язками рівняння х+bу = с. Отже, пара чисел виду (с –bу0; у0), 0 є Z, утворюють нескінченну множину розв’язків даного рівняння. Та все одно залишається відкритим питання: чи всі розв’язки отримані? Відповідь так! Адже якщо (x1;y1) – любий цілий розв’язок рівняння, тобто х1+bу1 = с – правильна рівність, то х1= с-bу1, тобто цей розв’язок може мати вигляд (с-bу1; у1 ), у1 є Z.
Для рівняння ах +у = с розмірковуємо аналогічно.
А далі використаємо це для розв’язку довільного діофантового рівняння
ах +bу = с,
де а, b – взаємно прості числа, зведемо до рівняння, де один із коефіцієнтів при невідомих дорівнює 1.
Отже, нехай існує розв’язок (x;y) даного рівняння і нехай а – менший по модулю із коефіцієнтів при невідомих (звичайно, можна вважати, що а – додатнє число). Розділивши з остачею b на а і с на а, запишемо ці числа у вигляді: b=aq1+r1 c=aq2+r2, де r1, r2 невідємні і менші за а числа.
Оскільки x=c-bya=aq2+r2-y(aq1+r1)a=q2-q1y+-r1y+r2a - ціле, то -r1y+r2a=t – цілий розв’язок даного рівняння зведено, по суті, до розв’язку діафантового рівняння –r1y+r2=at, 1≤r1<a. До цього рівняння застосуємо аналогічний прийом, в результаті якого отримаємо діофантове рівняння з ще меншими по модулю коефіцієнтами при невідомих.
Розглянемо декілька прикладів, щоб практично опанувати цей спосіб.
Приклад 1. Щоб застелити поли в сховищі довжиною7 м є дошки шириною 11см і 15см, відповідної довжини по ширині сховища. Скільки треба взяти дощок тієї та іншої ширини, щоб економно закрити підлогу.
Зрозуміло, що задача зводиться до розв’язку рівняння 11x+15y=700, де x –кількість дощок шириною 11см, а y – кількість дощок шириною 15см, причому, x і y – цілі (навіть натуральні) числа. Якщо рівняння має розв’язки, то
x=700-15y11=63∙11+7-11y-4y11=63-y+7-4y11. При цілих x і 63-y, t=7-4y11 – ціле. Звідси
11t+4y=7, або у=7-11t4=2-3t- 1-t4, 1-t4=u – ціле, 1-t=4u або t=1-4u, де u – ціле.
Таким чином, y=2-3t-u=2-3(1-4u)-u=-1+11u і x=63-y+t=63-(-1+11u)+(1-4u)=65-15u, де u – ціле число.
Розберемось в тому, що ми довели. А саме, якщо рівняння має розв’язки, то вони належать множині пар чисел (65-15u; -1+11u), u є Z. Виникають природні питання: чи всі ці пари задовольняють рівняння? А може лише деякі з них? А може й нема таких? Для відповіді на них скористаємось безпосередньою перевіркою.
11(65-15u)+15(-1+11u)=715-11∙15u-15+15∙11u=700.
Таким чином, всі пари (65-15u; -1+11u) при любих цілих і тільки вони є розв’язком даного рівняння.
Тепер проаналізуємо конкретні випадки та визначимось з остаточними розв’язками. Отже при u=0 ми отримали в якості розв’язку пару (65; -1), або x=65, y=-1. Але (-1) дошки в нашій задачі не має змісту, так як і 11x, і 15y повинні знаходитись в проміжку від 0 до 700. Розв’язки, що нам підійдуть отримуємо при u=1 тобто (40; 100), при u=2 - (35; 21), u=3 - (20; 32) і при u=4 - (5; 43)
Приклад 2. Знайти всі натуральні числа, що при діленні на 19 дають остачу 2, а при діленні на 17 – остачу 3.
Якщо x – шукане число, то що воно ділиться на 19 і дає остачу 2 можна записати так: x=19∙y+2, де y – неповна частка від ділення. Аналогічно, x=17∙z+3, де z – неповна частка від ділення з остачею числа х на 17. Звідси 19∙y+2=17∙z+3 або 19y-17z=1. Припустимо, що розв’язки рівняння є цілі числа, отримаємо:x=19y-117=y+2y-117y+t, де t=2y-117 – ціле. Звідси 2y-1=17t, y=17t+12=8t+t+12=8t+u, t+1=2u, t=2u-1, u – ціле. Тоді y=8t+u=8(2u-1)+u=17u-8, z=y+t=17u-8+2u-1=19u-9, u – ціле.
Перевірка показує, що всі пари (17u-8; 19u-9), u є Z, задовольняють дане рівняння. Насправді, 19(17u-8-17(19u-9)=-152+153=1.
Значення для шуканого числа х можна отримати, наприклад, із виразу x=19y+2:x=19(17u-8)=323u-152. Додатні цілі значення х, а саме про такі й ідеться в умові задачі, будемо мати при 323u-152>0, u>152323. На кінець маємо: 323∙u-152, u=1,2,3,…
Розглянутий метод розв’язку лінійних діофантових рівнянь з двома невідомими без великих змін переносимо на рівняння з більшим числом невідомих.
Так, розв’язком рівняння x+by+cz=d є всі трійки виду (d-by-cz;y;z), де y, z – довільні цілі числа, а якщо в рівнянні аx+by+cz=d всі коефіцієнти при невідомих відмінні від 1 (допускаємо, звичайно, що вони всі не нульові), то вибираємо серед них найменший по модулю – хай для визначеності це буде а – розглянемо x=d-by-cza і робимо, виділивши цілі вирази, так, як ми це робили для рівняння з двома невідомими з метою отримання рівняння з коефіцієнтом 1 біля невідомого. Розглянемо до даного матеріалу приклад.
Приклад 3. Розв’язати діофантове рівняння 3x+5y-8z=17.
Нехай дане рівняння має розв’язок x=17-5y+8z3=5-2y+2z+2+y+2z3. Тоді 2+y+2z3=t – ціле і y+2z-3t=-2. Розв’язком останнього рівняння можна подати у вигляді:
y=-2-2z+3t, z і t – довільні цілі. Звідси x=5-2y+2z+t=5-2∙(-2-2z+3t)+2z+t=9+6z-5t.
Таким чином, якщо розв’язки даного рівняння існують, то вони складаються із трійок виду (9+6z-5t; -2-2z+3t; z), (2)
де z і t – деякі цілі числа.
Робимо перевірку щоб упевнитись, що всі трійки чисел, отриманих із рівняння (2) при підстановці замість z і t – цілих значень, є рішеннями рівняння.
Необхідно зауважити, що при розв’язуванні діофантового рівняння ах +bу = с ми помічали, що якщо с не ділиться на НСД (а,b), то рівняння немає розв’язку цілими числами, а якщо с ділиться на НСД (а,b), то після скорочення рівняння на НСД (а,b) отримаємо рівносильне рівняння, в якому коефіцієнти при невідомих взаємно прості. Виникає питання: в останньому випадку чи обов’язково рівняння матиме розв’язок? В прикладах ми мали саме таку ситуацію і розв’язок знаходився. Відповісти на дане питання в загальному випадку допомагає алгоритм Евкліда для знаходження НСД (а,b). Адже процес послідовного виділення «цілих частин», запропонованого в методі розв’язку діофантових рівнянь, приводе до зменшення по модулю коефіцієнтів допоміжних рівнянь; що є залишками в алгоритмі Евкліда. А так як останній не дорівнює нулю залишок є НСД (а,b) і дорівнює 1, то обов’язково ми приходимо до допоміжного рівняння з коефіцієнтом 1 біля деякого невідомого, а отже це рівняння, а звідси і початкове обов’язково має розв’язок.
В літературі можна відшукати і інші способи розв’язування діофантових рівнянь.
Завдання для самостійної роботи.
1. Скількома способами можна заплатити 29 гривень купюрами по дві та п’ять гривень.
2. Чи має розв’язок діофантове рівняння 6x+18y=15.
3. Сума двох натуральних чисел дорівнює 168 і кожне з них ділиться на 24. Скільки пар чисел є розв’язками задачі.
4. Знайти цілі розв’язки рівняння
а) 8x-13y=63; б) 26x+34y=13; в) 39x-22y=10; г) 17x+13y+8z=89.
5. Знайти два додатні цілі числа, сума яких дорівнює 100 і одне із них ділиться на 7, а друге – на 11.
6. Найти всі числа, які при діленні на 23 дають остачу 3, а при діленні на 29 – остачу 5.
7. Найти число, яке при діленні на 3 дає остачу 2, а при діленні на 5 дає остачу 3, при діленні на 7 – остачу 2.
8. Знайти всі точки координатної площини з цілими координатами, що лежать на прямій АВ, А(-2;1), В(7;2). Скільки з них лежать на відрізку АВ?
9. Для перевезення рідини використовуються ємності 60л і 80л. Скільки було ємностей того та іншого об’ємів, якщо перевезли 440л рідини?
10. Знайти всі дроби з знаменниками 11 і 17, відповідно, такі, що їх сума дорівнює 97187.
11. Маємо три контейнера по 130кг і 160кг. Необхідно повністю загрузити ними вантажівку вантажопід’ємністю 3 тони. Як можна це зробити (вказати всі випадки)?
12. Знайти рік народження тих людей, яким в 1967 році виповнилось стільки років, яка сума цифр в році їх народження.
13. (задача Леонардо Пізанського) Купили 30 птахів за 30 монет, за кожних 3 горобці заплатили 1 монету, за кожні 2 горлиці – теж 1 монету, а за кожного голуба – по 2 монети. Скільки було птахів кожного виду?
9. РОЗГЛЯД ПРОБЛЕМ, ПОВ’ЯЗАНИХ З ПРОСТИМИ ТА ДОСКОНАЛИМИ ЧИСЛАМИ.
У теорії чисел час від часу виникають задачі, в яких вимагається довести той чи інший закон, що є правильним і перевіреним для багатьох частинних випадків. Як правило, такі задачі є настільки елементарними за своїм змістом, що зрозуміти їх може кожен школяр. Проте незважаючи на оманливу простоту формулювання, їх розв’язання роками, а іноді й століттями не піддається зусиллям найвидатніших математиків. Чимало таких проблем стосується саме простих чисел .
Як відомо, усі цілі числа залежно від кількості їх дільників можна розділити на 4 групи:
– числа, що мають лише 1 натуральний дільник (це числа 1 та -1);
– числа, які мають рівно 2 натуральних дільники (це, наприклад, числа: 2, -2, 3, -3, 5, -5,….) - їх називають простими;
– числа, в яких кількість натуральних дільників скінченна, але більша за два (наприклад: 4, -4, 6, -6, 9, -9,…) - такі числа називають складеними;
– числа, що мають нескінченну кількість натуральних дільників (це число нуль).
Зрозуміло, що досить розглядати лише додатні цілі числа. Виняткова роль простих чисел пояснюється тим, що вони виступають свого роду будівельним матеріалом для конструювання складених чисел. Тому й не дивно, що вони з давніх часів були предметом спеціального вивчення.
З часів Евкліда, математиків різних часів цікавило питання, за яким законом розподіляються прості числа у натуральному ряді. За словами відомого американського математика, фахівця з теорії чисел, Дона Цагіра, «прості числа ростуть серед натуральних, як бур'ян, підкоряючись випадку, і ніхто не може передбачити, де виросте наступне просте число».
Нерівномірність розподілу простих чисел виявляється у наступному:
– існує єдина пара послідовних простих чисел (2 і 3);
– є прості числа, різниця між якими рівна 2 (це так звані числа-близнюки: 3 і 5, 5 і 7, 11 і 13 тощо);
– відомо, що між числами n та 2 n ( n >7) міститься хоча б 1 просте число (так званий постулат Бертрана, сформульований у 1845 році.
Доведення цього факту було отримано значно пізніше, у 1852 році П. Чебишовим);
– існують проміжки, що включають мільйони натуральних чисел, серед яких немає жодного простого. Це, наприклад, ряд чисел: n! + 2, n! + 3, ..., n! + n, в якому кожне число ділиться на 2, 3,..., n відповідно.
Якщо розташувати натуральні числа по спіралі, можна побачити, що прості числа утворюють досить довгі ланцюжки вздовж діагоналей (так звана скатертина Улама). На рисунку 1 чорними точками позначено прості числа.
 (Рис.1)
(Рис.1)
Наведемо послідовність простих чисел починаючи з 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, … і т.д.
Згідно з основною теоремою арифметики кожне натуральне число, яке більше одиниці можна представити у вигляді добутку простих чисел. Разом з тим це є єдиним способом подання натуральних чисел з точністю до порядку проходження сомножителей. Виходячи з цього, можна сказати, що прості числа – це елементарні частини натуральних чисел.
Таке уявлення натурального числа називається розкладанням натурального числа на прості числа або факторизації числа.
Одним з найдавніших і ефективних способів обчислення простих чисел є «решето Ерастофен».
Практика показала, що після обчислення простих чисел за допомогою решета Ерастофен потрібно перевірити, чи є дане число простим. Для цього розроблені спеціальні тести, так звані тести простоти. Алгоритм цих тестів є ймовірними. Найчастіше їх застосовують в криптографії.
До речі сказати, що для деяких класів чисел існують спеціалізовані ефективні тести простоти. Наприклад, для перевірки чисел Мерсенна на простоту застосовують тест Люка-Лемера, а для перевірки на простоту чисел Ферма – тест Пепина.
Всі ми знаємо, що чисел нескінченно багато. Справедливо виникає питання: скільки ж тоді існує простих чисел? Простих чисел також нескінченну кількість. Найбільш древнім доказом цього судження є доказ Евкліда, яке викладено в «Засадах». Доказ Евкліда має наступний вигляд:
Уявімо, що кількість простих чисел звичайно. Перемножимо їх і додамо одиницю. Отримане число неможливо розділити ні на одне з кінцевого набору простих чисел, тому що залишок від ділення на будь-який з них дає одиницю. Таким чином, число має ділитися на деякий просте число, що не включене в цей набір.
Теорема розподілу простих чисел стверджує, що кількість простих чисел менших n, позначається π (n), росте як n / ln (n).
За тисячі років дослідження простих чисел, було виявлено, що найбільшим відомим простим числом є 243112609 – 1. Це число включає 12 978 189 десяткових цифр і є простим числом Мерсенна (M43112609). Це відкриття було зроблено 23 серпня 2008 року на математичному факультеті університету uCLA в рамках проекту по розподілених пошуку простих чисел Мерсенна GIMPS.
Головною відмінною рисою чисел Мерсенна є наявність високо ефективного тесту простоти Люка – Лемера. З його допомогою прості числа Мерсенна протягом тривалого періоду часу є найбільшими з відомих простих чисел.
Однак донині багато питань щодо простих чисел не отримали точних відповідей. На 5-му Міжнародному математичному конгресі Едмунд Ландау сформулював основним проблеми в області простих чисел:
Проблема Гольдбаха або перша проблема Ландау полягає в тому, що необхідно довести або спростувати, що кожне парне число, більше двох, може бути представлено у вигляді суми двох простих чисел, а кожне непарне число, більше 5, може бути представлено у вигляді суми трьох простих чисел.
Друга проблема Ландау вимагає знайти відповідь на питання: нескінченно чи безліч «простих близнюків» – простих чисел, різниця між якими дорівнює 2?
Гіпотеза Лежандра або третя проблема Ландау така: чи вірно, що між n2 і (n + 1) 2 завжди знайдеться просте число?
Четверта проблема Ландау: нескінченно чи безліч простих чисел виду n2 + 1?
Крім перерахованих вище проблем існує проблема визначення нескінченної кількості простих чисел в багатьох цілочисельних послідовностях типу числа Фібоначчі, числа Ферма і т. д.
Основний сферою докладання простих чисел є криптографія. Найбільшого поширення в цій області отримали прості числа порядку 10300. Крім цього прості числа використовуються в хеш-таблицях, а також для генерації псевдовипадкових чисел (зокрема, в ГПСЧ Вихор Мерсенна).
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ:
Германович П.Ю. Сборник задач по математике на сообразительность : [пособие для учителей] / Германович П.Ю. – М.: Учпедгиз, 1960. – 224с.
Голубев В.И. Решение сложных и нестандартных задач по математике / ГолубевВ.И. – М: ИЛЕКСА, 2007. – 252 с.
Канель-Белов А. Я., Ковальджи А. К., Как решают нестандартные задачи / Канель-Белов А. Я., Ковальджи А. К.; под редакцией В. О. Бугаенко. – [4-е Изд.] – испр.М.: МЦНМО, 2008. – 96с.
Математичнi олiмпiади i турнiри в Українi
Сборник задач киевских математических олимпиад / Вышенский В. А., КарташевН. В., Михайловский В. И., Ядренко М. И. – К.: 1984. – 240 с.
Башмакова І. Г. Діофант и діофантові рівняння. - М.: Наука, 1972 (Репринт М.: ЛКИ, 2007) (книга одного автора)
Сліпенко А. К. Лінійні рівняння і системи лінійних рівнянь. - Донецьк, 2009. – 32 с. (книга одного автора)
Диофант Александрийский. Арифметика и книга о многоугольных числах. Пер. И. Н. Веселовского; ред. и комм. И. Г. Башмаковой. М.: Наука (ГРФМЛ), 1974. 328 стр. (книга двох авторів)
З. І. Боревич , І. Р. Шафаревич, Теорія чисел. М., «Наука», 1964. (книга двох авторів)
Бородін О.І. Теорія чисел. Вид. 3-тє, переробл. і доп./О.І. Бородін – К.: Вища школа. 1970, – 275 с.
Валах В.Я. Подорож у світ цілих чисел./В.Я. Валах : – К.: Ред. загальнопед. газ., 2005. – 128 с. – (Б-ка «Шк. світу»).


про публікацію авторської розробки
Додати розробку