Даний посібник містить добірку завдань для проведення контролю знань, вмінь та навичок учнів з математики у 7 класі.
Даний посібник містить добірку завдань для проведення контролю знань, вмінь та навичок учнів з математики у 7 класі. Зміст контрольних робіт відповідає програмі з математики для загальноосвітніх навчальних закладів.
Завдання для контрольних і самостійних робіт подано у двох варіантах і розраховано на один урок, або частину уроку. Вчитель може змінювати обсяг і зміст завдань, враховуючи особливості класу та стан їх підготовки.
Головна мета цієї збірки – допомогти вчителю провести оцінювання знань учнів.
Діагностична контрольна робота. 7 клас.
1 варіант.
1. 1. Обчислити вираз: ( ![]() ) : ( -
) : ( -![]() ).
).
2. Накресліть координатну площину і позначте на ній точки А( 2; 3), В(2; -3), С(-4;-3), Д(-4; 3), з’єднайте точки у чотирикутник АВСД, та знайдіть його периметр.
3. Розв’яжіть рівняння: 3 ( 4 – 2х ) + 6 = - 2х + 4.
4. У першому ящику було в 5 разів більше мандаринів, ніж у другому. Коли з першого ящика взяли 25кг мандаринів, а в другий поклали ще 15кг, то в обох ящиках мандаринів стало порівну. Скільки кілограмів мандаринів було у кожному ящику спочатку?
5. ( додатково) У будинку 120 квартир, 25% з них становлять двокімнатні квартири. Скільки двокімнатних квартир у будинку?
2 варіант.
1. Обчислити вираз: ( ![]() ) : ( -
) : ( -![]() ).
).
2. Накресліть координатну площину і позначте на ній точки А(3; 4), В( 3; -2), С(-1; -2), Д(-1; 4), з’єднайте точки у чотирикутник АВСД, та знайдіть його периметр.
3. Розв’яжіть рівняння: 7х – 5( 2х + 1 ) = 5х +15.
4. На одній ділянці було у 3 рази більше саджанців, ніж на другій ділянці. Коли з першої ділянки увезли 30 саджанців, а на другу посадили ще 10 саджанців, то на обох ділянках саджанців стало порівну. Скільки саджанців було на кожній ділянці спочатку?
5.( додатково) У будинку 125 квартир, 20% з них становлять трикімнатні квартири. Скільки трикімнатних квартир у будинку?
Контрольна робота. Цілі вирази. Алгебра. 7 клас.
1 варіант.
1. Спростити вираз: 1) 5х2 + 8х – 7 – ( 2х2 – 2х - 12); 2) 2х – 3 – ( - 2х2 + 5х – 81);
3) 3х ( х3 – 4х + 6) ; 4) (х – 3)( 2х + 1); 5) (4а – 7в)(5а + 6в); 6) (у + 2)(у2 + у – 8).
2. Спростити вираз: 2а( 3а – 5) – (а - 3 )( а – 7).
3. Розв’язати рівняння: 1) (2х – 3)( х + 7) = (х – 4)( 2х + 3) + 4;
2) 14 – ( 1 + 3х - х2 ) = х2 + 4х – 8.
4. Обчисліть значення виразу, 18ху + 6х – 24у - 8 , при х = ![]() і у = 0,4.
і у = 0,4.
2 варіант.
1. Спростити вираз: 1) 8х2 – 12х + 4 – ( 2х2 + 5х – 2) ; 2) 11 + 2х + ( - х2 + 12х – 35);
3) – 5а( а4 – 6а2 + 3); 4) (х + 4)(3х – 2); 5) (6а + 5в)(7а – 3в); 6) (х + 5)( х2 +х – 6).
2. Спростити вираз: 7в( 2в + 3) – (в + 6)( в – 5).
3. Розв’язати рівняння: 1) (3х + 4)( 4х – 3) – 5 = ( 2х + 5)( 6х – 7);
2) 15 – ( 2х2 – 4х ) – ( 7х – 2х2 ) = 0.
4. Обчисліть значення виразу, 24ав + 32а – 3в , при а = 0,3 і в = - ![]() .
.
Контрольна робота. Степінь, одночлени. 7 клас.
1 варіант.
1. Обчислити вираз: 1,5 · 62 – 23 .
2. Спростити вираз: 1) х8 · х2 ; 2) х8 : х2 ; 3) ( х8 ) 2 ; 4) (( х4)5 · х2 ) : х12.
3. Приведіть одночлен до стандартного виду: 1) -3а2в4 · 3а2в5 ; 2) ( - 4а2в6 ) 3.
4. Обчисліть: 1) 212 · 29 : 220 ; 2) ( ![]() )5 · (
)5 · ( ![]() )5.
)5.
5. Спростити: 125а6в3 · ( - 0,2а2в4 )3.
6. Розв’язати рівняння: 4( 2х – 1 ) – 3х = 5х – 4.
2 варіант.
1. Обчислити вираз: 2,5 · 24 – 72 .
2. Спростити вираз: 1) х7 · х5 ; 2) х7 : х5 ; 3) ( х7 ) 5 ; 4) (( х3)6 · х4 ) : х18.
3. Приведіть одночлен до стандартного виду: 1) -4а3в5 · 5а2в4 ; 2) ( - 3а7в2 ) 4.
4. Обчисліть: 1) 310 · 39 : 318 ; 2) ( ![]() )7 · (
)7 · ( ![]() )7.
)7.
5. Спростити: 8х3у4 · ( - 0,5х2у5 )3.
6. Розв’язати рівняння: 2 ( 4х + 1) – х = 7х + 2.
Контрольна робота. Розкладання многочленів на множники. 7 клас.
1 варіант.
1. Розкласти на множники: 1) 5а2 – 20ав ; 2) 25х2 – 16 ; 3) 9х2 – 12ху + 4у2;
4) а3 + 27в3 ; 5) 3а – 3в + ах - вх .
2. Спростити вираз: ( х – 3)2 – (х – 1) ( х – 4) + ( х- 2) ( х + 2).
3. Розв’язати рівняння: 1) 4х2 – 12х = 0; 2) 6х3 – 24х = 0.
4. Довести, що число ділиться на 3 : 220 – 218 .
2 варіант.
1. Розкласти на множники: 1)18ху – 6х2 ; 2) 100 – 9х2 ; 3) 4а2 + 20ав + 25в2 ;
4) в3 - 8с3 ; 5) 3а + 3в + ха + хв.
2. Спростити вираз: ( х + 5) – ( х - 4) ( х + 4) + ( х – 3) ( х + 7).
3. Розв’язати рівняння: 1) 3х2 – 9х = 0 ; 2) 2х3 – 50х = 0.
4. Довести, що число ділиться на 8 : 312 - 310.
Контрольна робота з алгебри. 7 клас. Рівняння.
1 варіант.
1. Знайти корінь рівняння: 1) 9х – 7 = 6х + 14; 2) 3( 4 – 2х ) + 6 = - 2х + 4.
2. У першому ящику в 5 разів більше мандаринів, ніж у другому. Скільки кілограмів мандаринів в кожному ящику, якщо в двох ящиках разом 48 кг мандаринів?
3. Розв’язати рівняння: 1) 4( 2х – 1 ) – 3х = 5х – 4 ; 2) – 14х = 7; 3) ![]() х = 2,1.
х = 2,1.
4. За 3 ручки і 5 олівців заплатили 3 грн. 16 к. Скільки коштує 1 ручка і 1 олівець, якщо олівець дешевше за ручку на 68 к.?
2 варіант.
1. Знайти корінь рівняння: 1) 11х – 9 = 4х + 19; 2) 7х – 5( 2х + 1 ) = 5х + 15.
2. На одній ділянці в 3 рази більше кущів, ніж на другій. Скільки кущів на кожній ділянці, якщо на першій на 28 кущів більше, ніж на другій?
3. Розв’язати рівняння: 1) 2 ( 4х + 1 ) – х = 7х + 2; 2) 12х = - 6; 3) ![]() х = 3,6.
х = 3,6.
4. За 4 пачки печива і 3 пляшки мінеральної води заплатили 7 грн. 48 к. Скільки коштує 1 пачка печива і 1 пляшка води, якщо пачка печива дешевша за пляшку води на 58 к.?
Контрольна робота. Функції. 7 клас.
1 варіант.
1. Функція задана формулою у = -2х + 7. Знайдіть: 1) значення у, якщо х = 6;
2) значення х, якщо у = -9 .
2. Побудуйте графік функції у = 3х – 2 . За допомогою графіка визначте: 1) у,
якщо х = 2; 2) х, якщо у = -5 .
3. Не виконуючи побудови графіка функції, визначте координати точок перетину
графіка функції з осями координат функції у = 0,5х – 3 .
4. Функція задана формулою у = 1,6х – 2 , установіть, які з даних точок належать
графіку даної функції: А( 1; - 0,4 ), В( 2; 0,6), С( 5; 6), Д( -1,5; -3).
5. При якому значенні к , графік функції у = кх – 6, проходить через точку А( - 2; 20).
6. Побудуйте графіки функцій: 1) у = 2х; 2) у = - 3х.
2 варіант.
1. Функція задана формулою у = 8х - 3. Знайдіть: 1) значення у, якщо х = 2;
2) значення х, якщо у = -19 .
2. Побудуйте графік функції у = -2х + 5 . За допомогою графіка визначте: 1) у,
якщо х = 2; 2) х, якщо у = -1 .
3. Не виконуючи побудови графіка функції, визначте координати точок перетину
графіка функції з осями координат функції у = - 0,8х + 4.
4. Функція задана формулою у = -3,2х + 4 , установіть, які з даних точок належать
графіку даної функції: А( 2; - 2,4 ), В( 1; 0,8), С( 1; -0,8), Д( 0,5; 2,4).
5. При якому значенні к , графік функції у = -7х + к, проходить через точку А( - 2; 20).
6. Побудуйте графіки функцій: 1) у = 3х; 2) у = - 2х.
Контрольна робота. Системи рівнянь. 7 клас.
1 варіант.
-
Розв’язати систему рівнянь графічно:
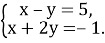
-
Розв’язати системи рівнянь: 1)
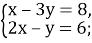 2)
2) 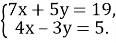
- За 3кг цукерок і 5кг печива заплатили 30грн, а за 2кг цукерок і 3кг печива заплатили 19грн. Скільки коштує 1 кг цукерок і 1 кг печива?
- варіант.
-
Розв’язати систему рівнянь графічно:
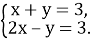
-
Розв’язати системи рівнянь: 1)
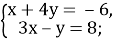 2)
2) 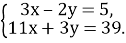
- За 5 ручок і 2 зошити заплатила 20 грн., а за 4 ручки і 4 зошити заплатили 28 грн. Скільки коштує 1 ручка і 1 зошит?
Самостійна робота. Вирази зі змінними. 7 клас.
1 варіант.
1.Знайти значення виразу: 1) 3х – 5, якщо х = 3; 2) ( 7 – 2х ) у, якщо х = 5, у = 2.
2. Заповнити таблицю:
|
х |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
|
5 – 3х |
|
|
|
|
|
|
|
2 варіант.
1.Знайти значення виразу: 1) 12 – 8х, якщо х = 4; 2) ( 3х – 5 ) у, якщо х = 3, у = 2.
2. Заповнити таблицю:
|
х |
- 3 |
- 2 |
- 1 |
0 |
1 |
2 |
3 |
|
3 – 2х |
|
|
|
|
|
|
|
|
Самостійна робота. 1 варіант. 1. Спростити вираз:
1) а5 · а3 = 2) х · х6 = 3) у3 · у8 · у5 = 4) а12 : а4 = 5) с8 : с = 6) ( ав)8 = 7) ( авс)10 = 8) ( а6)2 = 9) ( х4)3 =
2. Замініть зірочку числом, щоб отримана рівність була правильною:
1) а8 · а* = а13 , * = 2) а7 : а* = а3 , * = 3) а11 · а* · а = а16 , * =
|
Самостійна робота. 2 варіант. 1. Спростити вираз:
1) а4 · а3 = 2) х · х8 = 3) у2 · у6 · у4 = 4) а11 : а7 = 5) с6 : с = 6) ( ав)5 = 7) ( авс)9 = 8) ( а6)3 = 9) ( х2)5 =
2. Замініть зірочку числом, щоб отримана рівність була правильною:
1) а7 · а* = а11 , * = 2) а8 : а* = а3 , * = 3) а8 · а* · а = а12 , * = |
Самостійна робота. Степеня. 7 клас.
1 варіант.
1. Обчислити степінь: 1) 25; 2) 0,62; 3) (![]() )2; 4) (
)2; 4) (![]() )3; 5) (-7)2 ; 6) 72;
)3; 5) (-7)2 ; 6) 72;
7) (![]() )3 ; 8) (
)3 ; 8) (![]() )4.
)4.
1. Обчислити степінь: 1) 43 + 35 ; 2) (-8)2- (-1)10; 3) 7 · (![]() )2 ; 4) (-0,6)3 – (-0,5)3 ;
)2 ; 4) (-0,6)3 – (-0,5)3 ;
5) ( 63 : 400 + 0,33) : (-0,5)2 ; 6) ( 3,8 – 4,1 )4 · ( ![]() )3 .
)3 .
2 варіант.
1. Обчислити степінь: 1) 26; 2) 0,82; 3) (-![]() )4 ; 4) (
)4 ; 4) ( ![]() )2 ; 5) (-5)2; 6) 122;
)2 ; 5) (-5)2; 6) 122;
7) ( ![]() )3 ; 8) (
)3 ; 8) (![]() )3.
)3.
1. Обчислити степінь: 1) (-2)4 + 33; 2) (-5)2 + (-1)7 ; 3) 5 · ( -![]() )3 ; 4) (-0,4)3 + (-0,2)3;
)3 ; 4) (-0,4)3 + (-0,2)3;
5) ( 73 : 200 – 0,42 ) : ( -0,5)3; 6) ( 2,6 – 2,2 )3 · ( -![]() )2.
)2.
Самостійна робота. Додавання многочленів. 7 клас.
1 варіант.
Спростити вираз:
1) ( 6х2 – 7х + 4) – ( 4х2 – 4х + 18);
2) ( 3х + 9 ) + ( - х2 – 15х – 40) ;
3) ( 10а2 – 6а + 5 ) – ( - 11а + а3 + 6);
4) ( 13ху – 11х2 + 10у2) – ( - 15х2 + 10ху – 15у2);
5) ( 14ав2 – 17ав + 5а2в ) + ( 20ав – 14а2в );
6) ( х3 + 4у3 ) – ( у3 – 5ху + ( 3х3 – ( 3у2 + 6ху – 8х3 ))).
2 варіант.
Спростити вираз:
- ( 5х2 + 8х – 7) – ( 2х2 – 2х - 12 ) ;
- ( 2х - 3 ) – ( - 2х2 + 5х – 81) ;
- ( 6а2 – 3а + 11 ) – ( - 3а – а3 + 7 );
- ( 14ав – 9а2 – 3в2 ) – ( - 3а2 + 5ав – 4в2 );
- ( 7ху2 – 15ху – 3х2у ) – ( 30ху + 8х2у );
- ( 2а3 – 6в3 ) – ( 2а3 – 6ав – ( 5а3 - ( 3ав + 7в3 ))).
Самостійна робота. Винесення множника за дужки. 7 клас.
1 варіант.
1. Розкладіть на множники: 1) 8а – 12в ; 2) 3а – ав ; 3) 6ах + 6ау ; 4) 4а2 + 8ас;
5) а( х + у) – в( х+ у ) ; 6) х( 2а – 5в) + у( 2а - 5в).
2. Розв’язати рівняння: 1) х2 – 5х = 0; 2) х2 + 4х = 0; 3) 3х2 – х = 0.
2 варіант.
1. Розкладіть на множники: 1) 6а – 9в; 2) 4х – ху; 3) 5ав – 5ас; 4) 3х2 – 6ху;
5) х( а + в) + у( а + в) ; 6) а( 3х – 2у) + в( 3х – 2у) .
2. Розв’язати рівняння: 1) 3х – х2 ; 2) х2 + 5х = 0 ; 3) 11х2 – х = 0.
Самостійна робота. Множення многочленів. 7 клас.
1 варіант.
Перетворити вираз у многочлен: 1) ( а + 2) ( в – 3 );
2) ( m – 4) ( m + 5); 3) ( 3х – 1 ) ( 2х + 5);
4) ( 3в2 + 2) ( 2в – 4 ); 5) ( 4х – у ) ( 2х – 3у );
6) ( у + 3) ( у2 – 2у + 5); 7) 2х ( 3х – 1 ) ( 2х + 5).
2 варіант.
Перетворити вираз у многочлен: 1) ( х + 5) ( у – 7 );
2) ( х – 1 ) ( х + 5); 3) ( 3х – 5 ) ( 2х + 7);
4) ( 5х2 – 1 ) ( 5х + 1); 5) ( 5m – 2n ) ( 3m + n);
6) ( а – 3 ) ( а2 + 4а + 2 ); 7) х ( 2х – 1 ) ( 3х + 2).
Самостійна робота. Квадрат двочлена. 7 клас.
1варіант.
- Відкрити дужки: 1) ( х + 3)2 ; 2) ( 4 – у )2; 3) ( 2х – 5 )2 ; 4) ( 7а + 6в)2.
- Подайте у вигляді квадрата двочлена: 1) а2 + 8а + 16; 2) 9х2 – 6х + 1;
3) 121х2 – 88ху + 16у2; 4) 36а2 + 24ав + 4в2.
2варіант.
- Відкрити дужки: 1) ( а + 2)2 ; 2) ( 6 – х)2 ; 3) ( 3х – 4)2 ; 4) ( 5а + 3в)2.
-
Подайте у вигляді квадрата двочлена: 1) а2 – 14а + 49; 2) 25х2 + 10х + 1;
- 100а2 – 180ав + 81в2; 4) 16х2 – 56ху + 49у2.
Самостійна робота. Розв’язування рівнянь. 7 клас.
1 варіант.
Розв’язати рівняння: 1) 2х = 18 – х; 2) 7х + 3 = 30 – 2х; 3) 7 – 2х = 3х – 18;
4) 3( х – 2 ) = х + 2; 5) 3х + 6 = 2( 2х + 7) – х .
2 варіант.
Розв’язати рівняння: 1)4х = 24 + х; 2) 8х – 8 = 20 – 6х; 3) 9 – 4х = 3х – 40;
4) 4( х – 3 ) = х + 6; 5) 7х + 3 = 3( 2х – 1 ) + х.
Самостійна робота. Лінійні рівняння з двома змінними. 7 клас.
1 варіант.
1. Які з пар чисел (5; 8), (1; 4), (-3; 2) є розв’язками рівняння 3х – 4у = -17 ?
2. При якому значенні а пара чисел (1; -3) є розв’язком рівняння: 1) 2х – 7у = а;
2) 6х – ау = 4 ?
3. Чи належать графіку рівняння 4х – 5у = 30 точки А(1; - 4), В(0; -6), С(5; -2) ?
4. Побудувати графік рівняння 2х – у = 5.
2 варіант.
1. Які з пар чисел (3; 2), (-3; 2), (1,5; -1,5) є розв’язками рівняння 7х – 3у = 15 ?
2. При якому значенні а пара чисел (-1; 3) є розв’язком рівняння: 1) 5х – 3у = а;
2) 3х – ау = 6 ?
3. Чи належать графіку рівняння 3х + 5у = 15 точки А(5; 0), В(0; -3), С(1; 1) ?
4. Побудувати графік рівняння 2х + у = 5.
Самостійна робота. Системи рівнянь. 7 клас.
1 варіант.
- Розв’язати системи рівнянь:
-
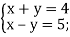 2)
2) 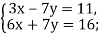 3)
3) 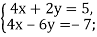 4)
4) 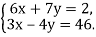
2 варіант.
1. Розв’язати системи рівнянь:
-
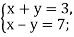 2)
2) 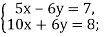 3)
3) 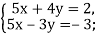 4)
4) 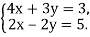
Самостійна робота. Розв’язування задач за допомогою систем рівнянь. 7 клас.
1 варіант.
1. Знайти два числа, сума яких дорівнює 10, а різниця дорівнює 4.
2. За 3 кілограми лимонів і 3 кілограми апельсин заплатили 15 гривен, а за 6
кілограмів лимонів і 1 кілограм апельсин заплатили 20 гривен. Скільки
коштує 1 кілограм лимонів і 1 кілограм апельсин?
2 варіант.
1. Знайти два числа, сума яких дорівнює 13, а різниця дорівнює 5.
2. За 2 кілограми цукерок і 3 кілограми печива заплатили 20 гривен, а за 4
кілограми цукерок і 1 кілограм печива заплатили 30 гривен. Скільки
коштує 1 кілограм цукерок і 1 кілограм печива?
Самостійна робота. Функція. 7 клас.
1 варіант.
1. Визначте, чи належать графіку функції у = 2х + 1 точки А( 1; 3) , В ( 5; 2), С ( 2; 5),
Д( 2; 3), Е( 3; 7), К( 4; 3).
2. Побудуйте графік функції: у = 2х + 1, при х = -2; -1; 0; 1; 2; 3; 4.
3. Функція задана формулою у = 2х – 1, заповніть таблицю:
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
у |
|
|
|
|
|
|
|
|
2 варіант.
1. Визначте, чи належать графіку функції у = 3х + 1 точки А( 1; 4) , В ( 5; 2), С ( 2; 7),
Д( 2; 3), Е( 3; 9), К( 4; 3).
2. Побудуйте графік функції: у = 3х + 1, при х = -2; -1; 0; 1; 2; 3; 4.
3. Функція задана формулою у = 3х – 1, заповніть таблицю:
|
х |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
у |
|
|
|
|
|
|
|
|
Контрольна робота. Розташування прямих на площині. 7 клас.
1 варіант.
1. Один з кутів, утворених при перетині двох прямих, дорівнює 60°. Знайти градусні міри решти кутів.
2. Один із суміжних кутів на 40° більший за другий. Знайдіть ці кути.
3. Через кінці відрізка АВ з одного боку від прямої АВ проведені промені АК і ВС так, щоб <КАВ = 107°, а <АВС = 73°. Чи паралельні промені АВ і ВС? Чому?
4. Один з суміжних кутів у 3 рази більший за другий. Знайдіть ці кути.
2 варіант.
1. Один з кутів, утворених при перетині двох прямих, дорівнює 120°. Знайти градусні міри решти кутів.
2. Один із суміжних кутів у 11 разів менший від другого. Знайдіть ці кути.
3. Через кінці відрізка АВ з одного боку від прямої АВ проведені промені АК і ВС так, щоб <КАВ = 87°, а <АВС = 93°. Чи паралельні промені АВ і ВС? Чому?
4. Один із суміжних кутів на 20° більший за другий. Знайдіть ці кути.
Контрольна робота. Трикутники. 7 клас.
1 варіант.
 1. Доведіть рівність трикутників АОВ і ДОС, А В
1. Доведіть рівність трикутників АОВ і ДОС, А В
якщо ОВ = ОС і <ОВА = <ОСД.
О
С Д
2. Периметр рівнобедреного трикутника дорівнює 26см, а основа – 8см. Знайдіть бічну сторону трикутника.
3. Знайдіть кути трикутника, якщо один з них у 2 рази більший за другий і у 3 рази менший від третього кута.
4. Знайдіть кути трикутника АВС, якщо <А + <В = 20° а <А + <С = 175°.
2 варіант.
 1. Доведіть рівність трикутників ХОУ і РОС, Х У
1. Доведіть рівність трикутників ХОУ і РОС, Х У
якщо ОУ = ОС і <ОУХ = <ОСР.
О
С Р
2. . Периметр рівнобедреного трикутника дорівнює 37см, а основа – 9см. Знайдіть бічну сторону трикутника.
3. Знайдіть кути трикутника, якщо один з них у 3 рази менший за другий і у 2 рази більший за третій кут.
4. Знайдіть кути трикутника АВС, якщо <А + <В = 123° а <А + <С = 158°.
Контрольна робота. Трикутники. 7 клас.
1 варіант.
1. Периметр рівнобедреного трикутника дорівнює 26см, а основа 8см. Знайдіть бічну
сторону трикутника.
2. Один з гострих кутів прямокутного трикутника у 3 рази більший за другий
гострий кут. Знайдіть ці кути.
3. У прямокутному трикутнику АВС катет АС = 14см, а <В = 30°. Знайдіть
гіпотенузу АВ.
4. В чотирикутнику АВСД АВ = СД і АД = ВС. Довести, що ΔАВД = ΔСДВ.
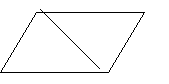 А В
А В
Д С 2 варіант.
1. Периметр рівнобедреного трикутника дорівнює 37см, а основа 9см. Знайдіть бічну
сторону трикутника.
2. Один з гострих кутів прямокутного трикутника у 2 рази більший за другий
гострий кут. Знайдіть ці кути.
3. У прямокутному трикутнику АВС гіпотенуза АВ = 16см, а <А = 30°. Знайдіть
катет ВС.
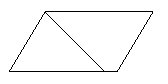 А В 4. В чотирикутнику АВСД АВ = СД і АД = ВС.
А В 4. В чотирикутнику АВСД АВ = СД і АД = ВС.
Довести, що ΔАВД = ΔСДВ.
Д С
Контрольна робота. Розв’язування трикутників. 7 клас.
1 варіант.
1. Периметр рівнобедреного трикутника дорівнює 42см, а основа трикутника
дорівнює 12см. Знайти бічну сторону трикутника.
2. Кути трикутника пропорційні числам 1, 2, 3. Знайти кути трикутника і визначити його вид.
3. У трикутнику АВС, <А = 500 , <В = 600. Знайти найбільшу сторону трикутника.
4. У прямокутному трикутнику АВС, <С = 900, <А = 600. На катеті ВС взято точку М,
так, що <АМВ = 600. Знайти ВМ, якщо СМ = 16см.
2 варіант.
1. Периметр рівнобедреного трикутника дорівнює 50см, а бічна сторона трикутника
дорівнює 15см. Знайти основу трикутника.
2. Кути трикутника пропорційні числам 1, 2, 2. Знайти кути трикутника і визначити його вид.
3. У трикутнику АВС, <А = 400 , <В = 500. Знайти найбільшу сторону трикутника.
4. У прямокутному трикутнику АВС, <С = 900, <А = 300. На катеті АС взято точку Е,
так, що <ВЕС = 600. Знайти АС, якщо ЕС = 8см.
Контрольна робота. Коло і круг. Геометричні побудови.7 клас.
1 варіант.
1. Діаметр кола дорівнює 12см. Знайдіть радіус кола.
2. Побудуйте трикутник АВС зі сторонами 6см, 4см і 5см.
3. У прямокутному трикутнику АВС гіпотенуза АВ = 38см, а <В = 60°. Знайдіть
катет ВС.
4. До кола з центром О проведено дотичну АВ ( В – точка дотику). Знайдіть радіус
кола, якщо АВ = 8см і <АОВ = 45°.
5. Відстань між центрами двох кіл дорівнює 9см. Визначте, скільки спільних
точок мають ці кола, якщо їх радіуси дорівнюють 6см і 4см.
2 варіант.
1. Діаметр кола дорівнює 24см. Знайдіть радіус кола.
2. Побудуйте трикутник АВС зі сторонами 6см, 5см і 3см.
3. У прямокутному трикутнику АВС гіпотенуза АВ = 20см, а <В = 60°. Знайдіть
катет ВС.
4. До кола з центром О проведено дотичну АВ ( В – точка дотику). Знайдіть радіус
кола, якщо АВ = 10см і <АОВ = 45°.
5. Відстань між центрами двох кіл дорівнює 9см. Визначте, скільки спільних
точок мають ці кола, якщо їх радіуси дорівнюють 2см і 4см.
Самостійна робота. Вертикальні і суміжні кути. 7 клас.
1 варіант.
1. Один із суміжних кутів у 4 рази більший за другий. Знайдіть ці кути.
2. При перетині двох прямих утворилися чотири кути, один з яких дорівнює 110°. Знайдіть всі інші кути.
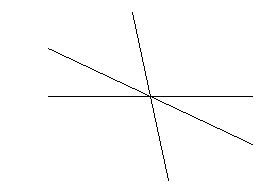 3. На рисунку <АОВ=50°, <СОД=25°. Знайти В
3. На рисунку <АОВ=50°, <СОД=25°. Знайти В
кут КОМ.
А
С
К О
Д
М
2 варіант.
1. Один із суміжних кутів у 3 рази більший за другий. Знайдіть ці кути.
2. При перетині двох прямих утворилися чотири кути, один з яких дорівнює 60°. Знайдіть всі інші кути.
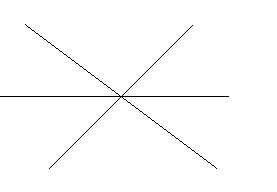 3. На рисунку <АОК=30°, <МОД=60°. К М
3. На рисунку <АОК=30°, <МОД=60°. К М
Знайти кут ВОС.
А
О Д
В С
Самостійна робота. Властивості паралельних прямих. 7 клас.
1 варіант.
1. Назвіть всі пари: внутрішніх односторонніх, різносторонніх і відповідних кутів.
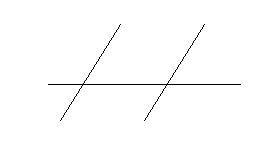
а в
1 2 5 6
с 4 3 7 8
2. Кут < 1 = 100°, а кут < 6 = 80°, чи паралельні прямі а і в?
2 варіант.
1. Назвіть всі пари: внутрішніх односторонніх, різносторонніх і відповідних кутів.
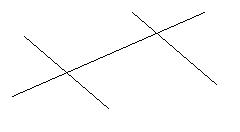 в с
в с
5 6
А 7 8
1 2
3 4
2. Кут < 8 = 70°, а кут < 2 = 80°, чи паралельні прямі а і в?
Самостійна робота. Рівнобедрений трикутник. 7 клас.
1 варіант.
1. Знайдіть периметр рівнобедреного трикутника, основа якого дорівнює 9см, а
бічна сторона 7см.
2. Периметр рівнобедреного трикутника дорівнює 19см, а основа дорівнює 7см.
Знайдіть бічні сторони.
3. Кут при вершині рівнобедреного трикутника дорівнює 48°. Знайдіть кути при
основі трикутника.
2 варіант.
1. Основа рівнобедреного трикутника дорівнює 5см, а бічна сторона 6см. Знайдіть
периметр трикутника.
2. Периметр рівнобедреного трикутника дорівнює 12см, бічна сторона трикутника
дорівнює 5см. Знайдіть основу трикутника.
3. Кут при вершині рівнобедреного трикутника дорівнює 84°. Знайдіть кути при
основі трикутника.
Самостійна робота. Прямокутний трикутник. 7 клас.
1 варіант.
1. Знайдіть другий кут прямокутного трикутника, якщо перший дорівнює 64°.
2. У трикутнику кути відносяться як 1 : 2 : 3. Доведіть, що трикутник прямокутний.
3. У прямокутному трикутнику АВС гіпотенуза АВ = 38см, а < В = 60°. Знайдіть катет ВС.
2 варіант.
1. Знайдіть другий кут прямокутного трикутника, якщо перший дорівнює 37°.
2. У трикутнику кути відносяться як 2 : 4 : 6. Доведіть, що трикутник прямокутний.
3. У прямокутному трикутнику АВС гіпотенуза АВ = 40см, а < В = 60°. Знайдіть катет ВС.
Самостійна робота. Трикутники. 7 клас.
1 варіант.
1. Периметр рівнобедреного трикутника дорівнює 32см, а основа дорівнює 12см.
Знайдіть бічну сторону трикутника.
2. Кути трикутника пропорційні числам 2, 4, 6. Знайдіть кути трикутника і визначте
його вид.
3. У прямокутному трикутнику АВС < С = 90°, < В = 30° а катет АС = 14см.
Знайдіть гіпотенузу АВ.
2 варіант.
1. Периметр рівнобедреного трикутника дорівнює 35см, а основа дорівнює 15см.
Знайдіть бічну сторону трикутника.
2. Кути трикутника пропорційні числам 3, 6, 9. Знайдіть кути трикутника і визначте
його вид.
3. У прямокутному трикутнику АВС < С = 90°, < А = 30° а катет ВС = 8см.
Знайдіть гіпотенузу АВ.
Самостійна робота. Сума кутів трикутника. 7 клас.
1 варіант.
1. Чи існує трикутник з кутами: 40°, 80°, 50°.
2. Знайдіть третій кут трикутника, якщо два його кути дорівнюють:
1) 53° і 62°; 2) 32° і 141° ; 3) 4° і 1°.
3. Знайдіть кути трикутника, якщо їх градусні міри відносяться як 3 : 4 : 5.
2 варіант.
1. Чи існує трикутник з кутами: 60°, 70°, 80°.
2. Знайдіть третій кут трикутника, якщо два його кути дорівнюють:
1) 42° і 54°; 2) 48° і 126° ; 3) 5° і 3°.
3. Знайдіть кути трикутника, якщо їх градусні міри відносяться як 3 : 5 : 4.
Самостійна робота. Перша ознака рівності трикутників. 7 клас.
1 варіант.
1. Відрізки АК і ДЕ перетинаються в точці В так, що АВ = ВД, КВ = ВЕ. Доведіть
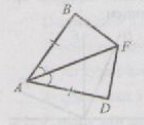 рівність трикутників АВЕ і ДВК.
рівність трикутників АВЕ і ДВК.
1. Доведіть рівність трикутників АВF і АДF, якщо АВ = АД, < ВАF = <ДАF. ( мал..)
2 варіант.
1. Відрізки АВ і СД перетинаються у точці К так, що АК = КВ, СК = КД.
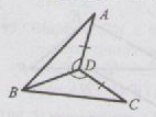 Доведіть рівність трикутників АКС і ВКД.
Доведіть рівність трикутників АКС і ВКД.
2. Доведіть рівність трикутників АВД і СДВ, якщо АД = ВС
і <АДВ = <СВД. ( мал..)
Самостійна робота. Трикутник і коло. 7 клас.
1 варіант.
1. Накресліть задовільний трикутник, опишіть навколо нього коло.
2. Накресліть задовільний трикутник і впишіть в нього коло.
3. Дан прямокутний трикутник АВС, зі сторонами 3см, 4см і 5см. Знайдіть довжину радіуса описаного навколо нього кола.
2 варіант.
1. Накресліть задовільний трикутник, опишіть навколо нього коло.
2. Накресліть задовільний трикутник і впишіть в нього коло.
3. Дан прямокутний трикутник АВС, зі сторонами 9см, 12см і 15см. Знайдіть довжину радіуса описаного навколо нього кола.
Самостійна робота. Коло і круг. 7 клас.
1 варіант.
1. Накресліть коло, радіус якого дорівнює 2,5см. Проведіть у ньому радіус, діаметр і
хорду.
2. Обчисліть діаметр кола, якщо його радіус дорівнює: 1) 3см, 2) 5,6см.
3. Обчисліть радіус кола, якщо його діаметр дорівнює: 1) 6см, 2) 9,6см.
4. Обчисліть довжину кола, якщо його радіус дорівнює 5см.
5. Обчисліть площу круга, якщо його радіус дорівнює 3см.
2 варіант.
1. Накресліть коло, радіус якого дорівнює 2см. Проведіть у ньому радіус, діаметр і
хорду.
2. Обчисліть діаметр кола, якщо його радіус дорівнює: 1) 2см, 2) 4,9см.
3. Обчисліть радіус кола, якщо його діаметр дорівнює: 1) 4см, 2) 7,8см.
4. Обчисліть довжину кола, якщо його радіус дорівнює 4см.
5. Обчисліть площу круга, якщо його радіус дорівнює 5см.
Самостійна робота. Задачі на побудову. 7 клас.
1 варіант.
1. Побудувати трикутник АВС, якщо АВ = 4см, ВС = 5см і АС = 6см.
2. Побудуйте прямокутний трикутник АВС, < С = 90°, з катетами АС = 5см і
ВС = 6см.
3. Побудуйте задовільний кут, і проведіть його бісектрису.
2 варіант.
1. Побудувати трикутник АВС, якщо АВ = 6см, ВС = 4см і АС = 7см.
2. Побудуйте прямокутний трикутник АВС, < С = 90°, з катетами АС = 6см і
ВС = 7см.
3. Побудуйте задовільний кут, і проведіть його бісектрису.


про публікацію авторської розробки
Додати розробку
