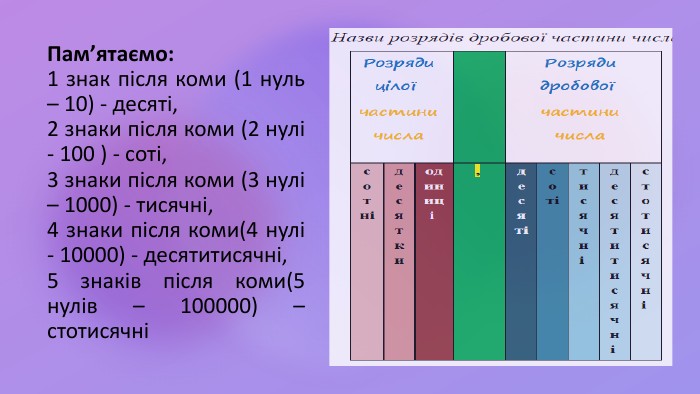
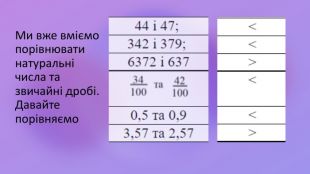
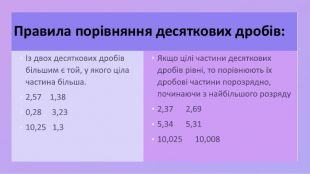
Десяткові дробі. Запис, читання та порівняння
Про матеріал
Презентація до уроку математики в 5 класі з теми "Десятковий дріб. Запис, читання та порівняння десяткових дробів. " за підручником Н.А.Тарасенової
Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку