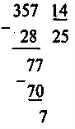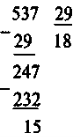Ділення з остачею. Площа прямокутника. Прямокутний паралелепіпед і його об'єм.

Тема. Ділення з остачею. Площа прямокутника. Прямокутний паралелепіпед і його об'єм.

Мета: перевірити засвоєння практичних знань та вмінь учнів з вивчених тем.

Тип уроку: перевірка й корекція знань, навичок і вмінь.

Обладнання: таблиці «Ділення з остачею», «Площа прямокутника», «Об'єм прямокутного паралелепіпеда».

Хід уроку

І. Тематична контрольна робота № 5

Варіант 1

1. Виконайте ділення з остачею: 357 : 14.
2. Знайдіть площу прямокутника, одна сторона якого дорівнює 16 см, а друга — в 3 рази довша за неї.
3. Обчисліть об'єм і площу поверхні куба із ребром 5 дм.
4. Довжина прямокутного паралелепіпеда 20 см, ширина — у 4 рази мен­ша від довжини, а висота — на 11 см більша за ширину. Обчисліть об'єм паралелепіпеда.
5. Чому дорівнює ділене, якщо дільник дорівнює 8, неповна частка 7, а остача 3?
6. Поле прямокутної форми має площу 36 а, його довжина 90 м. Об­числіть периметр поля.
7. Сума довжин усіх ребер прямокутного паралелепіпеда 156 см, два його виміри 11 см і 13 см. Обчисліть об'єм паралелепіпеда та площу його поверхні.

Варіант 2

1. Виконайте ділення з остачею: 537 : 29.
2. Знайдіть площу прямокутника, одна сторона якого дорівнює 72 см, а друга — в 4 рази коротша від неї.
3. Обчисліть об'єм і площу поверхні куба з ребром 6 см.
4. Ширина прямокутного паралелепіпеда дорівнює 13 см, довжина — на 17см більша за ширину, а висота — в 3 рази менша від довжини. Об­числіть об'єм паралелепіпеда.
5. Чому дорівнює ділене, якщо дільник дорівнює 8, неповна частка 9, а остача — 6?
6. Поле прямокутної форми має площу 54 а, його довжина 90 м. Об­числіть периметр поля.
7. Сума довжин усіх ребер прямокутного паралелепіпеда дорівнює 108 дм, два його виміри 7 і 11 дм. Знайдіть об'єм паралелепіпеда та площу його поверхні.

II. Домашнє завдання

№649; 609.

III. Розв'язання задач тематичної контрольної роботи № 5 і відповіді до них

Варіант 1

2. V = 16 · (16 · 3) = 768 (см²).

Відповідь. 768 см².

3. V = 5³ = 125 (см²); S_п = 6  · 5² = 150 (дм²).

Відповідь. 125 дм³; 150дм².

4. V = 20 · (20 : 4) · (20 : 4 + 11) = 20 · 516 = 1600(см³). Відповідь. 1600 см³.

5. а = 8 · 7 + 3 = 59.

6. 1) 36 а = 3600 м²;

2) 3600 : 90 = 40 (м) – ширина;

3) 2 · (90 + 40) = 260 (м) – периметр.

Відповідь. 260 м.

7.  4(а + b + с) = 156 см; а = 11см; b = 13 см; 4(11 + 13 + с) = 156;

4 (24 + с) = 156; 24 + с = 156 : 4; 24 + с = 39; с = 39 – 24; с = 15 (см).

V = abс; V = 11 · 13 · 15 = 2145 (см³); S_пов = 2(аb + bс + ас);

S_пов. = 2 · (11 · 13 + 13 · 15 + 11 · 15) = 1006 см².

Відповідь. 2145 см³; 1006 см².

Варіант 2

2. S = 72 · (72 : 4) = 72 · 18 = 1296 (см²).

Відповідь. 1296 см².

3. V = 6³ = 216 см³; S = 6 · 6² = 216 см². Відповідь. 216 см³; 216 см².

4. V = 13 · (13 + 17) · ((13 + 17) : 3) = 13 · 30 · 10 = 3900(см³).

Відповідь. 3900 см³.

5. а = 8 · 9 + 6 = 72 + 6 = 78. Відповідь. 78.

6.  1) 54 а = 5400 см²;

2) 5400 : 90 = 60 (м) – ширина поля;

3) Р= 2 · (90 + 60) = 300 (м) – периметр.

Відповідь. 300 м.

7.  4 · (а + b + с) = 108 (дм), де а = 7дм; b = 11 дм, тоді 4 · (7 + 11 + с) = 108;
4 · (18 + с) = 108; 18 + с = 108 : 4; 18 + с = 27; с = 27 – 18 = 9(дм).

V = аbс; V = 7 · 11 · 9 = 693(дм³);

S_пов. = 2(ab + bс + bс); S_пов. = 2 · (17 · 11 + 11 · 9 + 7 · 9) = 478 (дм²).

Відповідь. 693 дм³; 478 дм².