Правильні і неправильні дроби. Порівняння дробів.

Тема. Правильні і неправильні дроби. Порівняння дробів.

Мета: формувати поняття «правильний дріб», «неправильний дріб», встановити правила порівняння дробів з однаковими знаменниками; відпрацьовування вміння розрізняти правильні і неправильні дроби, за­стосовувати правило порівняння дробів із однаковими знаменниками і розв'язувати задачі, в яких передбачені ці дії.

Тип уроку: засвоєння знань, умінь, навичок.

Хід уроку

І. Перевірка домашнього завдання

Оскільки на попередньому уроці учнями була виконана і перевірена самостійна робота за темою «Уявлення про звичайні дроби», перевірку виконання домашнього завдання вчитель виконує, зібравши зошити учнів.

II. Актуалізація опорних знань
Запитання до класу

1. Як назвати записи: ; ; ?
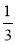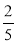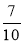2. Як називають число, записане внизу (зверху)?
3. Що показує знаменник дробу? Чисельник дробу?
4. На якому з відрізків, зображених на рис. 101, виділено 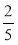відрізка? Яку частину відрізка виділено на інших відрізках?

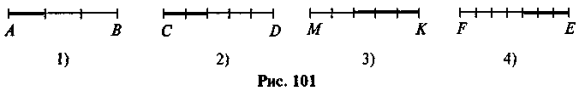
5. Яку частину становить:

1) довжина сторони квадрата від його периметра;

2) доба від високосного року;

3) кут, градусна міра якого 30°, від розгорнутого кута;

4) площа прямокутника зі сторонами 4 см і 25 см від 1 дм² ?

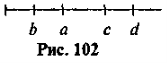6. Порівняйте числа а і b; b і с; с і d; a і d.
   Запишіть числа в порядку зростання (рис. 102).

III. Формування знань

Запитання до класу

1. На день народження Котигорошка мати спекла пиріг, який порівну поділили між десятьма запрошеними. Але Івасик-Телесик зателефо­нував, сказавши, що приїхати не зможе. Яку частину пирога отримав кожний з дев'яти прибулих гостей? Яка частина залишилась на долю Івасика-Телесика? Яку частину пирога з'їли всі присутні, якщо ніхто не відмовився і не просив добавки?

[Кожний отримав частину; залишилась частина, з'їли частин.]

2. На день народження Котигорошка мати спекла йому пиріг, який
   потім порівну поділила між десятьма гостями. Яку частину пирога з'їв
   кожний? Яку частину пирога було з'їдено, якщо ніхто не відмовлявся
   від частування?

[Кожний отримав частину, а всього з'їли частин.]

3. На день народження Котигорошка мати спекла йому два однакових пирога, обидва поділила порівну на 10 рівних частин за кількістю за­прошених. Гості з'їли по одному шматочку, а потім двоє з них: Хлопчик-мізинчик та Кіт у чоботях попросили по одному шматочку від другого пирога. Яку частину пирогів з'їли всі гості разом?

[Вони з'їли частин пирогів, бо кількість частин ділення — 10,

а кількість взятих таких частин — 12.]

Отже, виявляється, що:

1. чисельник дробу може бути меншим за знаменник 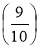, якщо кількість узятих частин менша від кількості частин ділення;
2. чисельник дробу може дорівнювати знаменнику 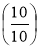, якщо взяти всі частини ділення, тому ;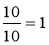
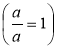3. чисельник дробу може бути більшим за знаменник (якщо взято не
   один, а декілька однакових предметів, які поділено на рівну кількість
   частин і взято кількість частин, більших від тієї, що складають цілий
   предмет).

Тому вчитель вивішує таблицю, (рис. 103) і звертається до таблиці, по­яснюючи, яка існує класифікація дробів — на закріплення.

Правильні і неправильні дроби. Порівняння дробів

Правильні дроби:         , де а < b; ; ; .

Неправильні дроби:     , де а > b; ; ; .

Порівняння дробів:      > , якщо а > с, > , бо 7 > 6;

> , якщо b < с, > , бо 10 < 16.

Рис. 103

Усні вправи

1. Які з дробів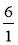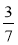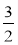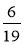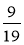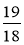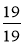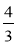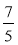: ; ; ; ; ; ; ; ; є правильними? неправильними?
2. Правильний чи неправильний буде дріб 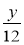, якщо:

1) у = 10; 2) у = 1; 3) у = 20; 4) у = 12?

3. Які координати мають точки Е, А, В, С, D (рис. 104)?

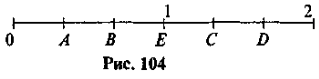
Які з цих точок лежать праворуч від т. Е;

ліворуч від т. Е; праворуч від т. А; ліворуч від усіх точок?

[Е(1) або Е ; A; В; C; D; праворуч від Е: С і D; ліворуч від Е: А і В; праворуч від А: точки В, Е, С, D; А лівіша від усіх цих точок; D — правіша від усіх точок.]

Отже, бачимо, що:

1) всі правильні дроби менші за неправильні ( < тощо);

2) всі правильні дроби менші за 1, а неправильні більші або дорівнюють 1;

3) із двох дробів з однаковими знаменниками більший той, в якого більший чисельник ( > , бо 2 > 1).

VI. Закріплення знань. Відпрацювання вмінь

№№ 694; 696; 698, крім 4), 5), 6); 700; додаткові задачі.

1. Два десятилітрових цебра повністю наповнені водою. З першого спо­чатку виливають 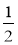цебра, а потім 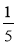остачі. З другого, навпаки, спочат­ку виливають 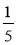цебра, а потім 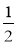остачі. В якому з цебер води залиши­лось більше?
2. З чисел 1; 4; 5; 7 утворіть:

а) всі можливі правильні дроби;

б) всі можливі неправильні дроби.

3. № 715 (підручник).
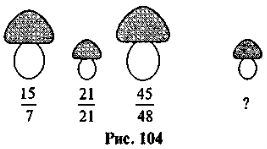
4. Яке     число      пропущено? (рис. 104)
5. Яке з чисел треба виключити?

; ; ; .

V. Підсумок уроку

Запитання до класу

1. Якщо в запису 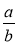а < b, то дріб 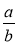називається....
2. Якщо в запису 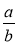а > b або а = b, то 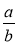називається ....
3. Яким повинен бути чисельник а, щоб дріб 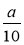був:

1) правильним;

2) неправильним;

3) меншим від ;

4) більшим від 1;

5) більшим від ?

VII. Домашнє завдання

п. 23, № 695; 697; 699 1); 3), 701, 10.