Розробка уроку на тему "Уявлення про звичайні дроби."

Тема. Уявлення про звичайні дроби.

Мета: формувати поняття про дробові числа, звичайні дроби; навчити учнів розпізнавати звичайний дріб, дробове число, читати й записувати звичайні дроби, розв'язувати нестандартні задачі на знаходження дробу від числа.

Тип уроку: засвоєння нових знань.

Обладнання: таблиця «Звичайні дроби».

Хід уроку

І. Актуалізація опорних знань

Усні вправи

1. Скільки:

1) у метрі — сантиметрів; дециметрів; міліметрів;

2) у годині — хвилин; секунд;

3) у тонні — кілограмів; центнерів; грамів?

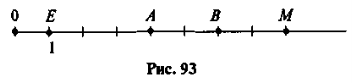
2. Знайдіть координати точок, зображених нарис. 93:

3. Знак якої арифметичної дії треба поставити замість *, щоб правиль­ною була рівність?

1) 75 * 1 = 75; 2) 2 * 2 = 4; 3) 79 * 0 = 79; 4) 37 * 0 = 0.

II. Засвоєння знань

1. Мотивація навчальної діяльності

 Учні п'ятого класу певною мірою знайомі з поняттям звичайного дро­бу, але перший урок теми все ж таки треба розпочати з того, що показа­ти учням необхідність введення поняття «дробові числа», запропону­вавши декілька практичних завдань (на кожну парту заздалегідь видано набір геометричних фігур).

Завдання 1. Як розділити відрізок, зображений у вигляді паперової смуги, на 2, 4, 8 рівних частин? [Скласти навпіл 1, 2, 3 рази]

Як знайти, чому дорівнює довжина кожної з утворених частин, якщо довжина смуги:  1) 8 см; 2) 16 см; 3) 10 см?  [1) 4, 2, 1 см; 2) 8, 4, 2 см; 3) 5 см; 10 : 4; 10 : 8 см]

Завдання 2. Як паперову модель кута по­ділити навпіл (провести бісектрису)?

[Треба скласти її по лінії, що виходить з вершини кута і перегнути так, щоб сторони даного кута співпали (рис. 94).]

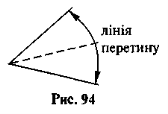Як знайти, чому дорівнює кут між бісектри­сою даного кута і його стороною, якщо даний кут: 1) прямий; 2) 72°; 3) 99°?

[1) 90° : 2 = 45^о;

2) 72^о : 2 = 36^о;

3) 99° : 2 не ділиться]

Завдання 3. Модель квадрата треба розрізати на 4 рівних частини. Як це зроби­ти, маючи тільки ножиці?

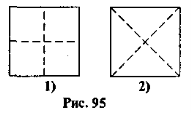[Можливі варіанти перетину квадрата на рис. 95]

Як знайти, чому дорівнює площа кож­ної з утворених частин, якщо сторона квадрата:

1) 10 см; 2) 2 см; 3) 1 дм?

[1)10² : 4 = 25см²; 2) 2² : 4 = 1см²;

3) 1² : 4 не ділиться]

Після виконання завдань учні (можна за допомогою вчителя) доходять висновку: розв'язання деяких математичних завдань приводить до не­обхідності введення нових, окрім натуральних, чисел — дробових.

Подальше викладення матеріалу відповідно до тексту підручника можна проводити за планом:

1. Поняття дробових чисел. Приклади дробових чисел, що зустрічають­ся в побуті.
2. Задачі, що приводять до поняття «звичайний дріб».
3. Запис звичайних дробів.
4. Що показує знаменник дробу? чисельник дробу?
5. Задача на знаходження частини одного натурального числа від іншого.
6. Задача на знаходження дробу від числа.

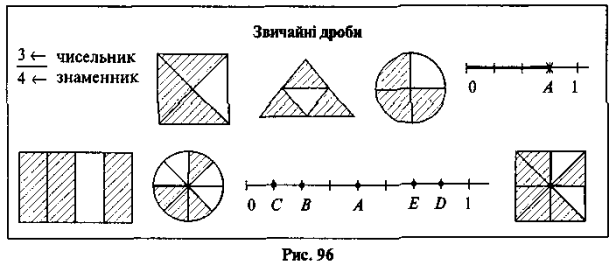
Свої пояснення вчитель супроводжує наочністю (таблиця «Звичайні дроби», рис. 96).

III. Закріплення матеріалу

 На першому уроці вивчення теми «Дроби» дуже важливо навчити учнів читати дроби, розпізнавати чисельник і знаменник дробу і розуміти, що показує кожний з них. Тому спочатку учні виконують вправи: №№ 651, 652, 653. (Коментар: учні повинні запам'ятати, що під час читання спо­чатку називають чисельник, а потім знамените, але якщо треба записати якесь число, що відповідає частині фігури у вигляді звичайного дробу .то спочатку краще встановити, чому дорівнює знаменник, порахувавши кількість рівних частин, на які воно поділено, а потім знаходимо чисель­ник, порахувавши кількість відлічених серед них частин).

Далі учні повинні навчитись записувати одиниці виміру у вигляді дро­бу (№ 655), але перш ніж давати учням це завдання, вчитель повинен про­вести деяку підготовчу роботу. А саме:

Завдання 4. Скільки в одному метрі сантиметрів (дециметрів, мілі­метрів)? На скільки рівних частин треба поділити відрізок довжиною 1 м, щоб отримати рівні частини довжиною 1 см (1 дм, 1 мм)?

Після виконання цього завдання учні самі (або за допомогою вчите­ля) складають своєрідний «алгоритм» розв'язання задач виду «Виразити величину меншими одиницями вимірювання».

1. Знайти, скільки в даній одиниці шуканих, і записати це натуральне число в знаменник дробу.
2. З'ясувати, скільки шуканих одиниць взяли, записати це натуральне число в чисельник дробу.

Наприкінці уроку учні розв'язують найпростіші задачі: № 657, 659, 661, 663, 664.

 Для кращого розуміння змісту розв'язання вправ № 657, 659 учням знову треба нагадати: коли щось ціле: сад, книжка тощо — поділено на рівні частини — дерева, сторінки, то кількість одиниць поділу є зна­менником дробу, а кількість «відмічених» одиниць є чисельником дро­бу. Тому в №657 маємо дріб ; а в № 659 спочатку знайдемо знамен­ник:

1)14 + 19 = 33 (с.) — уся книжка, а потім уже запишемо дроби: — перше оповідання; — друге оповідання.

№ 661, 663, 664 — найпростіші вправи на засвоєння алгоритму зна­ходження дробу від числа.

Додатково учням для засвоєння матеріалу, можна запропонувати логічну вправу.

Додаткове завдання. Вставити пропущений рисунок (рис. 97).

Рис. 97

IV. Підсумок уроку

Запитання до класу

1. Який запис називається звичайним дробом?
2. Що показує знаменник (чисельник) звичайного дробу? Де він запи­сується?
3. Скільки грамів: 1) у п'ятій частині кілограма; 2) у десятій частині кіло­грама?
4. Виразити у хвилинах: 1 сек; 20 сек; 59 сек.

V. Домашнє завдання

п. 12 до прикладу 3, №№ 654; 656; 658; 660; 662, повторення № 691 (1).