Дистанційний практикум з теми "Розв'язування систем лінійних рівнянь способом додавання"
Про матеріал
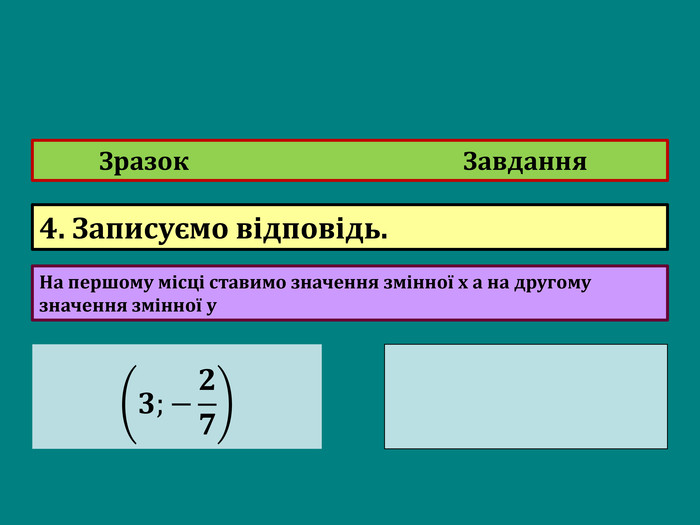
Дистанційний практикум складається з 5 блоків. У кожному з перших чотирьох блоків пропонується розв’язок зразка і завдання для самостійної роботи учнів за алгоритмом. У п’ятому блоці запропоновано оригінальний спосіб розв’язування системи лінійних рівнянь способом «подвійного додавання».
Матеріал можна використати для дистанційного навчання розбивши презентацію на блоки і зберігши кожну частину у pdf файл.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
Розв'язування систем лінійних рівнянь методом додавання Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку