Конспект на тему "Упрощение выражений".

1. Упрощение выражений
   1.         Порядок действий.

Скобки → Возведение в степень → Умножение и деление → Сложение и вычитание.

Слева направо.

1. Алгебраическая сумма.

2.       Одночлены. Приведение одночлена к стандартному виду.

Одночленами называют числа, переменные, их степени с натуральным показателем и их произведение.

Одночлен состоит из числового коэффициента и переменных.

Степень одночлена – сумма показателей степени всех переменных.

1. Произведение рациональных чисел.

Число, которое можно представить обыкновенной дробью вида , где m – целое, n – натуральное называется рациональным.

Натуральные числа – используемые при счете.

Целые числа – натуральные + отрицательные + ноль.

1.                   Умножение обыкновенных дробей.

Что бы умножить дробь на дробь, нужно числитель умножить на числитель, знаменатель на знаменатель.

Любое число или выражение можно записать в виде дроби со знаменателем 1.

1.            Смешанные числа.

Что бы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, а после умножить на дробь.

Что бы перевести смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель, и полученное произведение добавить в числитель, знаменатель оставить без изменений.

2.          Основное свойство дроби.

Основное свойство дроби: числитель и знаменатель дроби можно умножить или разделить на одно и тоже число.

1.    Сокращение дробей.

Сократить дробь, значит разделить числитель и знаменатель дроби на одно и тоже число.

2. Знак дроби.

2.                 Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, нужно их перемножить, не обращая на запятые, затем в ответе отделить запятой столько цифр, сколько их было после запятой у обоих чисел вместе.

Любое целое число можно представить в виде десятичной дроби

3.                 Арифметические действия с числами с одинаковыми и разными знаками.

Сложение и вычитание:

• Одинаковые знаки: складываем числа и ставим общий знак;
• Разные знаки: из большего по модулю вычитаем меньшее по модулю и ставим знак большего.

Умножение и деление:

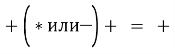
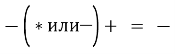
4.                 Сложение и вычитание дробей.

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить числители, а знаменатели оставить без изменений.

Чтобы сложить дроби с разными знаменателями, нужно привести дроби к общему знаменателю.

Приведение дробей к общему знаменателю.

1 способ.

 За общий знаменатель взять произведение знаменателей, числитель первой дроби умножить на знаменатель второй, числитель второй дроби на знаменатель первой.

2 способ.

Для приведения дробей к общему знаменателю:

• найти наименьшее число, что делится нацело на знаменатель первой и второй дроби (наименьшее общее кратное).

• разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;

• умножить числитель и знаменатели каждой дроби на ее дополнительный множитель.

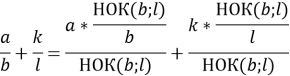
1.2.1.5 Стандартный вид одночлена

Стандартный вид одночлена – это одночлен, которые имеет один числовой множитель (коэффициент), записанный первым и степени переменных в единственном числе.

3.       Многочлен. Приведение многочленов к стандартному виду.

Многочлен – это сумма одночленов.

1. Раскрытие скобок.

• Произведение/Деление

Если перед(после) скобкой стоит знак умножения, значит всю скобку нужно умножить на множитель.

Если после скобки стоит знак деления, значит всю скобку нужно разделить на делитель.

• Знак

Если перед скобкой стоит:

Знак «+», знаки в скобке остаются без изменений.

Знак «-», знаки в скобке меняются на противоположные.

1.                   Смысл скобок.

2. Умножение одночлена на многочлен, многочлена на многочлен.

Что бы умножить одночлен на многочлен, нужно одночлен умножить на каждый член многочлена и полученные произведения сложить.

Что бы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.

3. Приведение подобных.

Слагаемые многочленов(одночлены), которые отличаются только коэффициентом, называются подобными членами(слагаемыми).

Привести подобные значит, сложить все подобные слагаемые.

4. Многочлен стандартного вида.

Многочлен стандартного вида – имеет только одночлены стандартного вида и не имеет подобных слагаемых.

4.       Тождества.

Тождество – равенство, выполняющееся на всем множестве значений входящих в него переменных.

Не любое равенство является тождеством.

Например, имеет место только при , поэтому оно не является тождеством.