ВЕСЕЛИНІВСЬКИЙ ЛІЦЕЙ

 

 

 

 

 

 

 

 

 

 

НАУКОВО-ДОСЛІДНИЦЬКА РОБОТА НА ТЕМУ:

 

«СТЕРЕОМЕТРІЯ В ЖИТТЄВИХ СИТУАЦІЯХ»

 

 

TRIAL

 

 

 

 

 

 

 

 

РОБОТУ ВИКОНАЛИ:

Гранченко Валерія

                                                                                                    Кушнір Станіслав

НАУКОВИЙ КЕРІВНИК:

                                                                                                Демешина Т.А.

 

 

TRIAL

 

 

 

 

 

 

 

 

 

 

ВЕСЕЛИНОВЕ-2024

ЗМІСТ

І. ВСТУП……………………………………………………………………..3-5 

ІІ. ЗАСТОСУВАННЯ ПОЛОЖЕНЬ СТЕРЕОМЕТРІЇ В РІЗНИХ ГАЛУЗЯХ:

2.1 Історія виникнення стереометрії ………………………………………6-7 2.2 Аксіоматичний підхід до дослідження навколишнього світу………..8-10

2.3 Практичне спрямування trial

TRIAL

-         Застосування стереометрії в архітектурі, машинобудуванні,

медицині……………………………………………………………….11-14

-         Прикладні задачі стереометрії ……………………………………… 15-16 

ІІІ. ВИСНОВКИ………………………………………………………………17

ІV. СПИСОК ВИКОРИСТАНИХ TRIAL ТА ЛІТЕРАТУРИ ……………18

ДОДАТКИ ………………………………………………………………………19

TRIAL

           

 

І. ВСТУП

 

Геометрія в нашому житті є на кожному кроці і відіграє дуже велику роль в житті кожної людини. З нею ми зустрічаємося не лише на уроках, вона знаходиться навколо нас, несе красу в наше життя. Геометрія бере участь у багатьох сферах людського життя і вносить свій вклад в ряд наук. А людині залишається тільки вчитися у природи – самого геніального винахідника. 

Геометрія - це про рух, збалансованість та стрункість простору навколо.

 

 

 

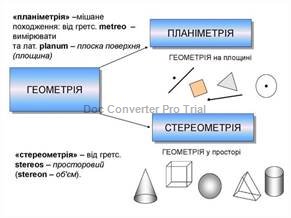
Стереометрія - це галузь геометрії, яка вивчає об'єми та площі геометричних тіл у тривимірному просторі. У повсякденному житті людина може зустрічати застосування стереометрії у таких ситуаціях, як обчислення об'єму басейну для заповнення водою, визначення об'єму ванної кімнати для підбору плитки чи обчислення об'єму коробки для відправлення пошти. Будьяка ситуація, де потрібно виміряти або розрахувати об'єм чи площу простору, може включати застосування стереометрії.

Варто відзначити широкий спектр можливостей, які відкриваються завдяки розумінню тривимірного простору. Стереометрія стає ключовим інструментом у таких галузях, як архітектура, інтер'єрний дизайн, інженерія, медицина, наука та багато інших. Розуміння стереометрії дозволяє краще аналізувати та моделювати об'єкти у тривимірному просторі, що має величезне значення для сучасних технологій та розвитку різних сфер діяльності.

 Дослідження trial стереометрії у різних галузях дозволить виявити перспективність цього інструменту та його вплив на сучасне суспільство. Окрім того, вивчення цієї теми дозволяє збагатити розуміння професійного оточення та розвинути креативний потенціал у створенні інноваційних рішень у різних галузях. Робота над аналізом та дослідженням застосування стереометрії у різних галузях є актуальним та перспективним завданням, яке сприятиме розвитку знань та навичок в цій області.

Отже, важливість trial проблеми, нагальна потреба дослідження та її вирішення зумовили вибір теми нашого дослідження:

«СТЕРЕОМЕТРІЯ В ЖИТТЄВИХ СИТУАЦІЯХ».

Об’єкт дослідження: застосування аксіоматичного підходу стереометрії до дослідження навколишнього світу.

TRIAL

Предмет дослідження: застосування теоретичних знань зі стереометрії в різних галузях людської діяльності 

Мета дослідження: застосування стереометрії в житті полягає в тому, щоб допомогти людям розв'язувати просторові задачі та вирішувати практичні проблеми, які вимагають розуміння тривимірного простору. 

Завдання дослідження: 

1.        Здійснити trial пізнання людиною навколишнього світу через застосування стереометричних моделей. 

2.        Розкрити trial положень стереометрії для кращого розуміння та роботи з тривимірними об'єктами у повсякденному житті. 

3.        Довести що застосування стереометрії в житті полягає в тому, щоб допомогти людям розв'язувати просторові задачі та вирішувати практичні проблеми, які вимагають розуміння тривимірного простору. 

Методи дослідження: 

1.   Експериментальний метод.

2.   Спостереження.

3.   Математичне моделювання.

Очікуванні результати:

Очікувані результати роботи зі стереометрією в повсякденному житті включають точні виміри, ефективне використання ресурсів та оптимальну організацію простору.

           

ІІ.    ЗАСТОСУВАННЯ     ПОЛОЖЕНЬ    СТЕРЕОМЕТРІЇ    В    РІЗНИХ

ГАЛУЗЯХ

2.1. Історія стереометрії

Виникнення геометрії сягає глибокої давнини і було обумовлено практичними потребами людської діяльності (необхідністю вимірювання земельних ділянок, вимірювання об'ємів різних тіл …) 

Стереометрія або геометрія в просторі - це розділ геометрії, що вивчає стан, форму, розміри і властивості різних просторових фігур.

Стереометрія - грецьке trial Воно походить від слів "стерео" - тіло і

"метрия"     -     вимірювати,     тобто     буквально     стереометрия     означає

"тіловимірювання". Trial як і планіметрія, виникла і розвивалася в зв'язку з потребами практичної діяльності людини. Про зародження геометрії в стародавньому Єгипті близько 2000 років до н.е. давньогрецький вчений Геродот (V ст. до н.е.) писав наступне: "Сеозоостріс, єгипетський фараон, розділив землю, дав кожному єгиптянину ділянку по жеребу і стягував відповідним чином податок з кожної ділянки. Траплялося, що Ніл заливали ту чи іншу ділянку, тоді потерпілий звертався до царя, а цар посилав землемірів, щоб встановити, на скільки зменшилася ділянка, і відповідним чином зменшити податок. Так виникла геометрія в Єгипті, а звідти перейшла до

Греції ". 

Однією з найперших і найвідоміших шкіл була піфагорійская (VI-V вв.до н. Е.), Названа так на честь свого засновника Піфагора. Для своїх філософських теорій піфагорійці використовували правильні багатогранники, форми яких надавали елементам першооснов буття, а саме: вогонь - тетраедр, земля - гексаедр (куб); повітря - октаедр; вода - ікосаедр; весь Всесвіт, на думку древніх, мав форму додекаедра.

TRIAL

У сучасному розумінні стереометрія стала важливою дисципліною геометрії, яка використовується як у наукових дослідженнях, так і в повсякденному житті. Зараз безліч математичних моделей, теорем та формул, заснованих на принципах стереометрії, застосовуються в архітектурі, інженерії, комп'ютерній графіці та інших областях, пов'язаних із тривимірним простором та об'єктами.

Вчені, які стояли у витоків стереометрії 

Учений	Рік
Герон	3 століття до н.
Архімед	3 століття до н.
Евклід	3 століття до н.
Аполлоній Пергський	3-2 століття до н

 

TRIAL

           

2.2. Аксіоматичний підхід до дослідження навколишнього світу

Геометрія - це математична ідеальна модель навколишнього світу. І пізнаючи та вивчаючи ці моделі людина тим самим пізнає навколишній світ. Але, всьому в природі є свій початок. В даному дослідженні розглянемо як геометрія і аксіоматичний підхід допомагають вивчати навколишній світ.

Аксіоматичний підхід у trial є ключовим для дослідження навколишнього тривимірного простору, оскільки встановлення початкових аксіом, на яких ґрунтується весь процес розуміння та побудова геометричних моделей, дозволяє ретельно та систематично досліджувати просторові відношення та властивості об'єктів. Цей підхід сприяє створенню консистентної та логічної структури вивчення стереометрії, яка дозволяє точно та об'єктивно аналізувати тривимірні об'єкти та процеси у них. Шляхом застосування аксіоматичного підходу у стереометрії, дослідники можуть отримати важливі знання про тривимірний простір та його властивості, що допомагає зрозуміти навколишній світ більш повно та об'єктивно. Розглянемо застосування деяких аксіом стереометрії: 

 

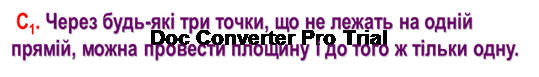
Застосування: 

üТабуретка із трьома ніжками завжди ідеально стане на підлогу і не буде гойдатися. У табуретки з чотирма ніжками бувають проблеми зі стійкістю, якщо ніжки стільця не однакової довжини. Табуретка розкачується, тобто опирається на три ніжки, а четверта ніжка (четверта «точка») не лежить в площині підлоги, а висить в повітрі (рис.1). 

üДля відеокамери, фотозьомки, пьюпітра і для інших пристроїв часто використовують штатив – триногу. Три ніжки штатива стійко розміщуються на будь-якій підлозі в приміщеннях, на асфальті або прямо на газоні на вулиці, на піску на пляжі або в траві в лісі. Три ніжки штатива завжди знайдуть площину (рис.2). 

üРухома площина дверей, що проходить через дві фіксовані точки A і B, розташовані в місцях кріплення завісів до одвірка, фіксується (стає визначеною) третьою точкою якого-небудь обмежника: наприклад, кілочком C у підлозі для запобігання вдаряння об стіну, або замком D у протилежному одвірку (рис.3). 

 

                                         

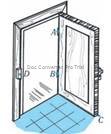
                      рис. 1                               рис. 2                         рис. 3

 Стіл, який має 5 ніжок замість 3. Дизайнер не

застосував аксіому стереометрії, тому собівартість такого стола збільшилася.

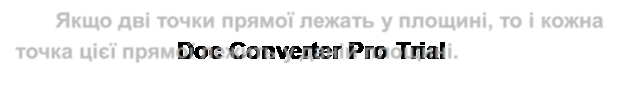 С_շ. Якщо дві точки прямої лежать у площині, то і кожна точка цієї прямої лежить у даній площині.

  

TRIAL

üВластивість, сформульована в аксіомі С₂ на практиці застосовують, наприклад, для вишивання: для того, щоб  пряма нитка щільно прилягала до поверхні тканини, натягненої на п’яльці, тканину проколюють у двох місцях (рис.4).

üTrial сформульована в аксіомі С2 на практиці застосовують, наприклад, для вишивання: для того, щоб  пряма нитка щільно прилягала до поверхні тканини, натягненої на п’яльці, тканину проколюють у двох місцях (рис.5).                                                                                                                                            рис. 4                                                      рис. 5                                    

С_ᶾ. Через дві прямі, що перетинаються, можна провести площину і до того ж тільки одну

üПрактичну цінність цього твердження ілюструє такий приклад: під час рятування потопаючого на тонкій кризі рятувальник має розпластатися на площині криги у вигляді літери Х, щоб його вага розподілялася рівномірно і крига не провалювалася (рис. 6).

 

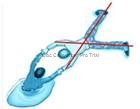
рис. 6

TRIAL

С . Якщо дві різні площини мають спільну точку, то вони

4

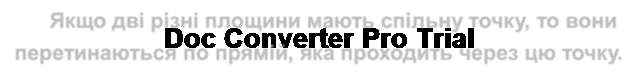перетинаються по прямій, яка проходить через цю точку.

Наочною ілюстрацією аксіоми С₄ є перетин двох суміжних стін, стіни і стелі класної кімнати, стіни і підлоги (рис. 7).

 

рис. 7

           

2.3. Практичне застосування стереометрії:

- Застосування стереометрії в trial машинобудуванні, медицині

Застосування стереометрії в житті має величезне значення для розвитку різних галузей. Цей метод не лише допомагає вирішити практичні завдання, але і сприяє пошуку нових рішень та покращенню якості життя.

Архітектура:

Знання кутів у стереометрії може бути корисним у таких сферах, як архітектура та будівництво. А саме знання про двогранний кут.

              

Архітектори використовують кути для створення стійких і естетично привабливих конструкцій, тоді як будівельники покладаються на точні вимірювання, щоб переконатися, що будівлі будуються правильно та витримують різні сили. В архітектурі та будівництві стереометрія відноситься до вимірювання тривимірних об'єктів і просторів. Наприклад, архітектори використовують стереометрію для розрахунку об’єму, площі поверхні, кутів і пропорцій будівель і споруд. Це допомагає їм створювати точні креслення та проекти будівельних проектів. 

Для розрахунку стійкості будівлі використовуються різні методи і принципи, включаючи і стереометрію. Одним із  кроків у розрахунку стійкості будівлі є етап «визначення опори». Стереометрія допомагає визначити геометричні параметри будівлі, такі як довжина, ширина та висота, які впливають на співвідношення опорних точок та реакцій опор.

Одним із поширених прикладів стереометрії в архітектурі є використання програмного забезпечення для 3D-моделювання для візуалізації та планування будівель перед їх будівництвом. 

Один із способів застосування знань про стереометрію в повсякденному житті

– це дизайн інтер’єру. Під час проектування кімнати чи простору розуміння поняття об’єму може допомогти визначити, скільки меблів чи декору можна помістити в просторі, не створюючи відчуття переповненості. 

Знання площі поверхні також може бути корисним при визначенні кількості фарби або шпалер, які потрібні для покриття стін кімнати. Навіть найменші деталі можуть внести необхідного яскравого акценту, задавши гармонійний ритм інтер’єру.

Машинобудування

Тіла обертання широко застосовуються в техніці, особливо в машинобудуванні, автомобілях, тракторах та в їх обладнанні. Найпростіша деталь автомобіля — підшипник (рис.8) — має в своєму складі тіло обертання - кулю. Але чому саме кулю, а не куб або призму? Та тому, що куля зазнає найменшого тертя під час роботи підшипників. У них вставляються кульки однакового розміру. Не можна вставити хоча б одну кульку більшу або меншу за розміром, бо це спричиняє люфт агрегатів і призводить до ушкоджень. Важливим є також те, що складові частини кермової трапеції з’єднані не простими болтами, а кульовими з’єднаннями Бо під час повороту змінюються кути з’єднання і циліндричні болти можуть зламатися .

Важливу роль в машинобудуванні відіграють циліндри. Циліндричні підшипники в автомобілях використовують там, де потрібні підшипники з великою бічною поверхнею і невеликою товщиною (наприклад, у механізмі зчеплення). У формі циліндра зроблено найважливіші складові частини: генератор, індукційну котушку, конденсатори, фільтри, насоси, стартер, карданну передачу, гідро підсилювач тощо. Тут використовується така властивість обертання навколо своєї осі: відстань від усіх зовнішніх точок до осі обертання однакова, що якраз ми спостерігаємо у циліндрі.

В рух транспортний засіб приводять двигуни внутрішнього згоряння. Головні робочі частини двигуна — поршні —теж мають форму циліндрів і знаходяться в своєрідних циліндрах. Під час переміщення поршня від верхньої мертвої точки до нижньої мертвої точки над ним утворюється простір, який називається робочим об’ємом циліндра. Коли поршень знаходиться у верхній мертвій точці, над ним утворюється найменший простір, який називається об’ємом камери згоряння. У багатоциліндрових двигунах повний об’єм усіх циліндрів виражається в літрах і називається літражем. Таким чином, визначення об’ємів циліндрів є головною характеристикою автомобіля (рис.

TRIAL

10)

Чи trial в машинобудівництві конуси? У формі конусів виконано регулюючі гвинти урізних частин тракторів (наприклад, на колесах). Використовуються також конічні підшипники. Голчасті клапани, виготовлені у формі конуса, використовуються у карбюраторі для регулювання подачі палива. У вигляді конуса виготовлені деякі деталі двигуна (головки клапанів, кульові пальці, поршень у головному гальмовому циліндрі) (рис.11).

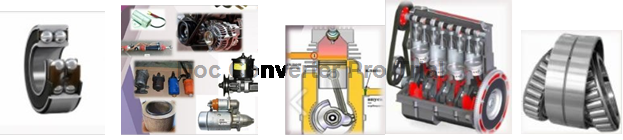    рис. 8              рис. 9                                   рис. 10                              рис. 11

Усе це свідчить про те, що такі тіла обертання, як куля, циліндр, конус, широко застосовуються в обладнанні автомобілів та тракторів. Як сказав видатний французький архітектор Ле Корбюзі, ми живемо в геометричний період і навколо нас – геометрія. І справді, світ в якому ми живемо, наповнений геометрією будинків і вулиць, творінням природи і людини. Квітникарю, інженеру, архітектору, водію- всім необхідна геометрична уява. Тіла обертання також знайшли широке застосування у повсякденному житті, науці і техніці.

Медицина

В медицині стереометрія використовується для створення тривимірних моделей органів та структур людського тіла, що дозволяє лікарям отримувати детальніший та більш об'єктивний образ для діагностики, планування лікування та проведення хірургічних втручань. Наприклад, використання стереометрії у рентгенології дозволяє отримати тривимірні образи внутрішніх органів, що полегшує визначення патологічних змін та вибір оптимального методу лікування. Також стереометрія застосовується в стоматології для планування імплантації, виробництва зубних протезів та інших медичних процедур.

           

- Прикладні задачі стереометрії

Задача №1 Для установки опалювальної системи в будинку потрібно розмістити  радіатори з розрахунку: три одиниці на 50 м³. Яку кількість одиниць радіаторів необхідно замовити  для нового будинку, якщо він має фому прямокутного паралелепіпеда з розмірами 15 мХ20мХ30 м?

Розв’язання: Будинок має форму прямокутного паралелепіпеда. Тому:

1.        Визначаємо об’єм будинку за формулою об’єму прямокутного паралелепіпеда V=abh.  V=9000мᶾ.  

2.        Визначаємо кількість радіаторів: 9000:50=180.

Відповідь: потрібно 180 радіаторів.

 

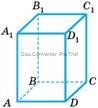
Задача №2 Скільки потрібно картону для виготовлення одного ковпака для святкування дня народження, якщо  обхват голови дитини 60см, а висота ковпака 20см?

Розв’язання: trial має форму конуса. Тому

1.     Обчислюємо радіус основи конуса, застосовуючи формулу довжини кола: С=2ПR;  R=C/2П; 𝑅 = 60 ÷ (2 ∙ 3,14) = 9,6см.

2.     Trial довжину твірної конуса за теоремою Піфагора 𝑙² = ℎ² + 𝑅².

TRIAL

𝑙 = 22,2см. 

3.     Обчислюємо площу бічної поверхні конуса за формулою 𝑆 = П𝑅𝑙. 

S=669,2cм²

Відповідь: потрібно 669,2см² картону для виготовлення одного ковпака.

 

 

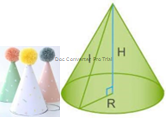
Задача №3. Скільки повних порцій борщу міститься в каструлі, яка має форму циліндра, висота якого 60 см, а діаметр 50см? Відомо, що одна порція містить 0,25л борщу.

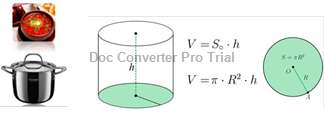 Розв’язання: каструля має форму

TRIAL

циліндра. Тому:

1.     Обчислимо об’єм циліндра: V=117750см³=0,11775м³.      

2.     Обчислимо N - кількість порцій в каструлі: 0,25л = 2,5 ∙ 10 ⁻⁴м³.

N= 0,11775: 2,5∙ 10⁻⁴= 490,63.

Відповідь в каструлі міститься 490 повних порцій

TRIAL

 

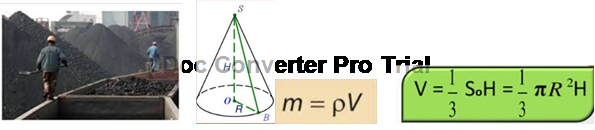
Задача №4 Ви керівник підприємства. Постачальник, вказуючи на купу вугілля, що має конічну форму, пропонує вивезти її, запевняючи , що в ній певна кількість тон. Які виміри та  обчислення потрібно виконати, щоб впевнитися, що вас не обманюють? 

Розв’язання: купа вугілля має конічну форму. Тому:  

1.     Trial довжину кола в основі купи вугілля та обчислити довжину радіуса.

2.     Виміряти висоту купи вугілля (конуса).

3.     Обчислити об’єм, який займає вугілля.

4.     За таблицями визначити густину вугілля та обчислити за формулою

TRIAL

𝑚 = р ∙ TRIAL масу вугілля.

 

 

ІІІ. ВИСНОВКИ

На основі проведеного дослідження щодо застосування положень стереометрії в повсякденному житті  нами встановлено: стереометрія грає важливу роль у різних сферах життя, допомагаючи людям розв'язувати складні просторові завдання та вирішувати практичні проблеми. У повсякденному житті знання стереометрії, вивчення тривимірних форм і вимірювання їхніх властивостей, можуть виявитися неймовірно корисними. Розуміння таких понять, як об’єм, площа поверхні та кути, може допомогти нам у різних практичних ситуаціях. Таким чином: 

 

•      Вивчення стереометрії допомагає розвивати просторове мислення, уявлення про просторові відношення та форми об'єктів, що є корисним для різних професій.

•      Стереометрія має практичне значення для побуту та допомагає в повсякденних ситуаціях, де важливе розуміння тривимірного простору.

•      Вивчення стереометрії сприяє розвитку  творчості, дозволяючи ефективно втілювати ідеї у тривимірному просторі.

•      Вивчення стереометрії розширює знання та навички у сфері математики та вдосконалює логічне мислення.

           

ІV. СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ ТА ЛІТЕРАТУРИ

1.     Алла Прус Василь        Швець        ПРИКЛАДНА     СПРЯМОВАНІСТЬ

                СТЕРЕОМЕТРІЇ     10—11     клас    Київ     «Шкільний    світ»    2007р.

                [Електронний              ресурс]              –              Режим              доступу:

http://eprints.zu.edu.ua/20268/1/Prus_Prykladna_spryamovanist_stereometri ji.pdf

 

2.     https://formula.co.ua/blog/tag/tsitati/

 

3.     https://uk.wikipedia.org/wiki/%D0%A1%D1%82%D0%B5%D1%80%D0%

B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D1%96%D1%8F

 

4.     «Практичні завдання на уроках математики» Бондаренко Т.Ф., учитель математики загальноосвітньої школи № 17 м. Слов’янська Донецької області

 

5.     https://moyamebel.com.ua/ua/blog/geometriya-v-interere-za-i-protiv ДОДАТОК №1

Експериментальне дослідження:

1.     Перевірка стійкості триноги якщо всі її «ноги»:

а) мають однакову довжину;

б) різні довжини.

            

           а)                                                             б)  

Висновок: Тринога стійка, оскільки всі три точки опори лежать в одній площині.  

TRIAL

2.     Перевірка стійкості конструкції з 4 дротиків, якщо всі її «ноги» мають:

а) однакові довжини;

б) різні довжини.

               

           а)                                                                         б)

Висновок: конструкція з 4 однаковими «ніжками» стійка. Але якщо «ніжки» різної довжини, то стійкість порушується, оскільки, четверта ніжка не лежить в площині основи.