Контрольна робота з геометрії для сімейного навчання 10 клас 2 семестр
Контрольна робота з геометрії для сімейного навчання 10 клас 2 семестр
Перпендикулярність у просторі. Координати та вектори у просторі.
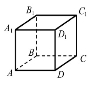
- На рисунку зображено куб АВСD А1В1С1D1. Укажіть проекцію похилої А1С на площину (А1АВ)
|
А) А1С1 |
Б) А1В |
В) АС |
Г) D1С |
Д) А1D |
- З точки В до площини α проведено похилу ВС, яка утворю з площиною α кут 30°. Знайдіть відстань від точки В до площини α, якщо проекція похилої ВС на цю площину дорівнює 12 см.
|
А) 6 см |
Б) |
В) |
Г) 24 см |
- На рисунку зображено куб АВСD А1В1С1D1 (див. завдання 1). Знайдіть кут між прямими АВ1 і СD1
|
А) 60° |
Б) 45° |
В) 0° |
Г) 90° |
- Яка з наведених точок лежить у площині oxz прямокутної системи координат у просторі.
|
А) (0; -3; 0) |
Б) (0; 4; -3) |
В) (3; 0; -4) |
Г) (-4; 3; 0) |
Д) (-3; 3; 3) |
-
Обчисліть скалярний добуток векторів
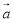 (3; 2; -1) і
(3; 2; -1) і  (-1; -4; 5)
(-1; -4; 5)
|
А) 120 |
Б) 26 |
В) 0 |
Г) -10 |
Д) -16 |
-
Знайдіть вектор
 =2
=2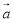 -
- , якщо
, якщо 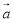 (3; -1; 2),
(3; -1; 2),  (-2; 2; 5)
(-2; 2; 5)
|
А) |
Б) |
В) |
Г) |
Д) |
- Знайдіть координати точки М, відносно якої симетричні точки E (-3; 8; 7) і F (-9; 6; 1)
|
А) (-6; 7; 4) |
Б) (-12; 14; 8) |
В) (0; 0; 0) |
Г) (3; 1; 3) |
Д) інше |
- У прямокутній декартовій системі координат задано точку М (1; -4; 8). Знайдіть відстань від точки М до осі z.
|
А) 1 |
Б) 4 |
В) |
Г) 8 |
Д) 9 |
- З точки А до площини проведено похилі АВ і АС та перпендикуляр АК. АВ=10 см, ВК=6см, КС=15 см. Знайдіть АС.
|
А) |
Б) 17 см |
В) 25 см |
Г) |
-
Який із запропонованих векторів перпендикулярний до вектора
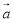 (-2; 3; -1)
(-2; 3; -1)
|
А) |
Б) |
В) |
Г) |
- Кут між площинами дорівнює 60°. Точка А лежить в площині α. Знайдіть відстань від точки А до площини β Якщо відстань від точки А до лінії перетину площин дорівнює 6 см.
|
А) |
Б) |
В) |
Г) |
Д) |
-
Знайдіть площу проекції многокутника на задану площину якщо площа многокутника
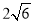 см2 а кут між даною площиною і площиною многокутника дорівнює 30°.
см2 а кут між даною площиною і площиною многокутника дорівнює 30°.
|
А) |
Б) |
В) |
Г) |
Д) 6 см2 |
-
Точка М знаходиться поза площиною прямокутного трикутника на однакових відстанях від його вершин. Знайдіть відстань від точки М до вершин трикутника, якщо відстань від точки М до площини трикутника 12 см,
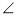 С=90°, АС=8 см, ВС= 6 см.
С=90°, АС=8 см, ВС= 6 см.
-
Точка М знаходиться на відстані
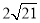 см від площини трикутника АВС і рівновіддалена від прямих що містять сторони трикутника. Проекцією точки М на площину трикутника АВС є точка О, яка належить даному трикутник. Знайдіть відстань від точки М до прямої АВ, якщо АВ=11 см, ВС=25 см, АС=30 см.
см від площини трикутника АВС і рівновіддалена від прямих що містять сторони трикутника. Проекцією точки М на площину трикутника АВС є точка О, яка належить даному трикутник. Знайдіть відстань від точки М до прямої АВ, якщо АВ=11 см, ВС=25 см, АС=30 см.
- Точки А (2; 0; -3), С (-6; 0; -1), D (5; 5 ; 2) вершини паралелограма АВСD. Знайдіть координати вершини В.
- Знайдіть зовнішній кут при вершині В трикутника АВС, якщо відомі координати вершин А (0; 2; -2), В (0; -1; 1), С (1; -1 ; 0)
- Діагоналі ромба з тупим кутом при вершині В дорівнюють 30 см і 40 см. Відрізок МВ перпендикуляр до площини ромба, МВ= 24 см. Знайдіть кут між площиною ромба і площиною (СМD).
-
Знайдіть косинус кута між векторами
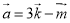 і
і 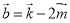 якщо
якщо  і
і  .
.
-
Точки А і В лежать у перпендикулярних площинках α і β відповідно. З точок А і В опущено перпендикуляри АА1 і ВВ1 на лінію перетину площин, АВ1=
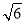 см, АВ=
см, АВ=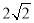 см, АА1=2 см. Знайти кути, які утворює відрізок АВ з площинами α і β.
см, АА1=2 см. Знайти кути, які утворює відрізок АВ з площинами α і β.
Геометрія 10 клас. Оцінювання завдань
|
Номери завдань |
Кількість балів |
Усього балів |
|
1 – 12 |
По 1 б |
12 |
|
13 – 16 |
По 2 б |
8 |
|
17 – 19 |
По 3 б |
9 |
|
Сума балів |
29 |
|
|
Кількість набраних балів |
Оцінка за 12-бальною системою оцінювання навчальних досягнень учнів |
|
0 – 2 |
1 |
|
3 – 4 |
2 |
|
5 – 6 |
3 |
|
7 – 8 |
4 |
|
9 – 10 |
5 |
|
11 – 12 |
6 |
|
13 – 16 |
7 |
|
17 – 20 |
8 |
|
21 – 24 |
9 |
|
25 – 26 |
10 |
|
27 – 28 |
11 |
|
29 |
12 |


про публікацію авторської розробки
Додати розробку
