Довідковий матеріал до теми "Подібність трикутників"
ГЕОМЕТРІЯ, 8 ТЕМА 2. П О Д І Б Н І С Т Ь Т Р И К У Т Н И К І В
Означення.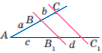 Відрізки називають пропорційними, якщо пропорційні їх довжини.
Відрізки називають пропорційними, якщо пропорційні їх довжини.
Відрізки a і b пропорційні відрізкам c і d, якщо правильна пропорція ![]()
Узагальнена теорема Фалеса
Паралельні прямі, що перетинають сторони кута, відтинають на його сторонах пропорційні відрізки.
Якщо BB1 || CC1 і кут CAC1 (BAC і CAC, а B1AC1 і C1AC1 ), тоді ![]() або
або ![]()
Наслідок 1. ![]() . Наслідок 2.
. Наслідок 2. ![]()
Подібні трикутники
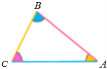 Означення. Два трикутники називають подібними, якщо їх кути відповідно рівні і сторони одного трикутника пропорційні відповідним сторонам другого трикутника.
Означення. Два трикутники називають подібними, якщо їх кути відповідно рівні і сторони одного трикутника пропорційні відповідним сторонам другого трикутника.
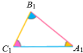 А1 = A, B1 = B, C1 = С,
А1 = A, B1 = B, C1 = С,
![]()
Лема. Пряма, паралельна стороні трикутника, відтинає від нього трикутник, подібний даному.
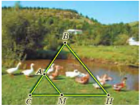
566. Знайдіть відстань між двома садибами (позначимо їх А і В),
які розташовані на протилежних берегах річки (див. рис.),
якщо АМ || BH і CA = 4 м, CM = 5 м, MH = 35 м.
Ознаки подібності трикутників
За двома сторонами і кутом між ними За двома кутами За трьома сторонами
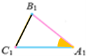
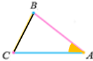
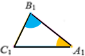
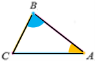
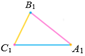
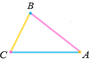
А1 = A, ![]() А1 = A, B1 = B
А1 = A, B1 = B ![]()
Властивість медіан та бісектриси трикутника
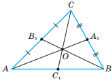
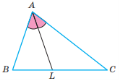
Якщо О – точка перетину медіан ABC, то![]() . Якщо AL – бісектриса ABC, то
. Якщо AL – бісектриса ABC, то ![]()
Ознаки подібності прямокутних трикутників
За двома катетами За гострим кутом За гіпотенузою і катетом
![]()
![]()
![]()
![]()
![]()
![]()
Середні пропорційні відрізки у прямокутному трикутнику
Відрізок k називають середнім пропорційним відрізків m і n, якщо k2 = m ![]() n.
n.
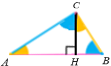
Лема. Висота прямокутного трикутника, проведена з вершини прямого кута, розбиває трикутник
на два подібних прямокутних трикутника, кожний з яких подібний даному трикутнику.
![]()
ACH ![]() CBH, CH2 = AH
CBH, CH2 = AH ![]() HB. ACH
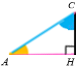
HB. ACH ![]() ABC, AC2 = AB
ABC, AC2 = AB ![]() AH. ABC
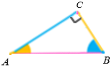
AH. ABC ![]() CBH, BC2 = AB
CBH, BC2 = AB ![]() BH.
BH.
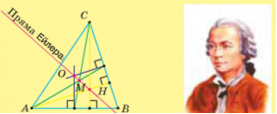 Теорема. У будь-якому трикутнику центр описаного
Теорема. У будь-якому трикутнику центр описаного
кола О, точка перетину медіан М (центроїд) і точка перетину висот трикутника H (ортоцентр) лежать
на одній прямій.
Теорему про пряму, названу його ім’ям, Леонард Ейлер сформулював, довів й опублікував у 1765 р.
Леонард Ейлер (1707-1783)
-
-
Велике спасибі за чудовий матеріал і титанічну працю!
-


про публікацію авторської розробки
Додати розробку
