Довідник з математики

Про матеріал

Усі формули для вивчення. Окремо виділені за темами. Документ у форматі WORD.

Перегляд файлу

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Відокремлений структурний підрозділ «Костянтинівський коледж Луганського національного аграрного університету»

Воронцова О.М., Мірошніченко Г.І.
Корнюшенко Р.С., Ткаченко М.В.

Підготовка до ЗНО

(Довідник з математики)

Затверджено

на засіданні циклової комісії

загальноосвітніх дисциплін

протокол № ___ від _______

Голова ЦК _________ О.М. Акулова

с. Іллінівка, 2019

Дійсні числа

Позначення:

N – множина натуральних чисел. Числа, які використовуються при лічбі.

Z – множина цілих чисел. Натуральні числа 1, 2, 3, …, їм протилежні числа -1, -2, -3, … і число 0 утворюють множину цілих чисел.

Q – множина раціональних чисел. Числа, які можна подати у вигляді , де , .

I – множина ірраціональних чисел. Ірраціональні числа – нескінченні неперіодичні десяткові дроби ().

R – множина дійсних чисел. Об’єднання національних та ірраціональних чисел називають дійсними числами.

Парні та непарні числа

Числа виду a=2n, де n – натуральне число, називаються парними.
Вони діляться на 2 без остачі.

Числа виду a=2n+1, де n – натуральне число, називаються непарними.
Непарне число при діленні на 2 дає остачу 1.

Деякі ознаки подільності натуральних чисел

Число ділиться на 2, якщо його остання цифра є число парне або нуль.

Число ділиться на 3, якщо сума цифр числа ділиться на 3.

Число ділиться на 4, якщо дві його останні цифри – нулі або утворюють число,

яке ділиться на 4.

Число ділиться на 5, якщо воно закінчується на нуль або на 5.

Число ділиться на 6, якщо воно ділиться на 2 і на 3.

Число ділиться на 9, якщо сума його цифр ділиться на 9.

Число ділиться на 10, якщо воно закінчується на нуль.

Число ділиться на 11, якщо сума його цифр, що стоять на парних місцях,

дорівнює сумі цифр, що стоять на непарних місцях або відрізняється від неї на

число, яке ділиться на 11.

Число ділиться на 25, якщо дві його останні цифри – нулі або утворюють число,

яке ділиться на 25.

Ознака подільності суми. Якщо кожен із доданків ділиться на натуральне число

b, то і сума ділиться на b.

Ознака подільності добутку. Якщо хоч один із співмножників ділиться на

натуральне число b, то і добуток ділиться на b.

Властивості натуральних чисел

Властивості додавання:

1) a+b=b+a (переставний закон додавання);

2) (a+b)+c=a+(b+c) (сполучний закон додавання).

Властивості множення:

1) a·b=b·a (переставний закон множення);

2) (a·b)·c=a·(b·c) (сполучний закон множення);

3) (a+b)·c=a·с+b·c (розподільний закон множення).

Найбільший спільний дільник (НСД) та

найменше спільне кратне (НСК) кількох натуральних чисел

НСД – це найбільше з чисел, на які діляться число a і число b.

НСК – це найменше число, яке ділиться як на число a, так і на число b.

Числа a і b називаються взаємно простими, якщо НСД(a,b)=1.

Формула зв'язку НСД і НСК двох натуральних чисел a і b:
ab= НСД(a,b)НСК(a,b).

Середні значення чисел

Середнє арифметичне n чисел: , (.

Середнє геометричне n чисел: ,
.

Для двох чисел: ; .

Гармонічне n чисел: ; двох чисел ..

Квадратичне n чисел: ; двох чисел .

Дроби

Правила дії з дробами: 1) ; 2) ;
3) ; 4) .

Основна властивість дробу:

Формула перетворення скінченного десяткового дробу в раціональний дріб:

0,, де – цифри.

Формула перетворення нескінченного періодичного десяткового дробу в

раціональний дріб:

0,.

0,8(172) = 5,8(12)=5,812121212… = 12,34(5) =

Пропорції

Пропорція має вигляд , або a:b=c:d, де ad – крайні члени; b, c – середні члени пропорції.

Властивості пропорції: , , , , , , , m, n, p, q – будь-які числа та .

Дві величини називають прямо пропорційними, якщо зі збереженням значень однієї з них у кілька разів значення другої збільшується у стільки ж разів.

Дві величини називають обернено пропорційними, якщо із збільшенням значень однієї з них у кілька разів значення другої зменшується в стільки ж разів.

Відсотки

Відсоток – це одна сота: 1%=0,01, 50%=0,5, 100%=1.

Знаходження p відсотків від числа а: а=100%, х=р%, х= .

Знаходження числа за його відсотком: нехай р% деякого числа у дорівнюють числу а, тоді а=р%, у=100%, у= .

Знаходження процентного відношення двох чисел a і b: .

Формула складних відсотків: , де – початковий капітал; – капітал через років; – число відсотків.

Степені та їх властивості

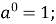
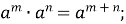
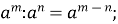
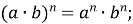
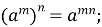
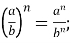
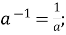
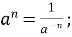
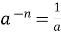Корені та їх властивості

Якщо a і b невід'ємні, то:

1) =;

2) =;
3) == ;

4) = ;
5) =;
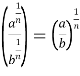6) ;

7) = ;

8) .=.

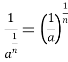Якщо a і b невід'ємні, то: =;.

Логарифми

Логарифм даного числа у при основі а є показник х, до якого треба піднести а, щоб одержати у: .

Основна логарифмічна тотожність: .

Властивість логарифмів:

1) ;

2) ;

3) , ;

4) , ;

5) , , непарне;

6) , , парне;

7) , , , ;

8) , , , ;

9) , , , , , ;

10) , , , , .

Десятковий логарифм – логарифм за основою 10: .

Натуральний логарифм – логарифм за основою , де – число Непера: .

Зв'язок між десятковими і натуральними логарифмами:

Формули скороченого множення

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) , де – будь-яке натуральне число;

10) , де – парне натуральне число;

11) , де – непарне натуральне число.

Формули скороченого множення із коренями

1) ;

2) ;

3) ;

4) ;

5) .

Звільнення від ірраціональності в знаменнику

1) ;

2) ;

3) ;

4) ;

5) .

Алгебраїчні рівняння

Лінійне рівняння , де . Розв'язок: .

Квадратне рівняння: , де

Дискримінант .

Якщо , то рівняння має два різні дійсні корені: .

Якщо , то рівняння має один корінь, тобто корінь кратності 2.

Біквадратне рівняння підстановкою зводиться до квадратного рівняння 1); 2)

Способи розкладання на множники

Квадратний тричлен при розкладається на множники:

Якщо , то розклад має вигляд: .

Винесення спільного множника за дужки .

Спосіб групування .

Формули Вієта

Формули Вієта для зведеного квадратного рівняння

Для незведеного квадратного рівняння формули мають вигляд:

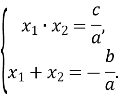
Формули Вієта для зведеного кубічного рівняння

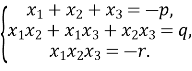
Алгебраїчні нерівності

Строгі нерівності: Нестрогі нерівності:

Якщо то .

Властивості нерівностей:

1) якщо то ;

2) якщо і то ;

3) якщо , то

4) якщо і то

5) якщо і то

6) якщо і то

Лінійні нерівності:

де

Розв'язок нерівності

1) якщо то (рис. 1);

2) якщо то (рис. 2).

Рис. 1 Рис. 2

Деякі важливі нерівності

1) (нерівність трикутника);

2) ;

3) ;

4) , де – дійсні числа одного знаку;

5) (середнє арифметичне невід'ємне чисел більше або дорівнює їх середньому геометричному);

6) , де – гармонічне; – геометричне; арифметичне; – квадратичне;

7) нерівність Бернуллі , де ,

Квадратні нерівності

Квадратні нерівності мають вигляд: ; ; ; де

Розв'язок нерівності :

1) при і , (рис. 3);

2) при і , (рис. 4);

3) при і , (рис. 5);

4) при і , (розв'язків немає) (рис. 6).

Рис. 3 Рис. 4

Рис. 5 Рис. 6

Функція

Залежність змінної у від змінної х називається функцією, якщо кожному значенню х відповідає єдине значення у. Змінну х називають незалежною змінною або аргументом, а змінну у – залежною змінною.

Усі значення, які приймає незалежна змінна, утворюють область визначення функції; усі значення, які приймає залежна змінна, утворюють множину значень функції.

Графік функції в обраній системі координат – це множина всіх точок, абсциси яких дорівнюють значенням аргументу, а ординати відповідають значенням функції.

Основні характеристики функцій

Монотонність.

Функція зростає на даному числовому проміжку Х, якщо більшому значенню аргументу , відповідає більше значення функції , тобто для будь-яких точок і із проміжку X таких, що , виконується нерівність .

Функція спадає на даному числовому проміжку Х, якщо більшому значенню аргументу відповідає менше значення функції , тобто для будь-яких і таких, що , виконується нерівність .

Функція, яка тільки зростає або тільки спадає на даному числовому проміжку, називається монотонною на цьому проміжку.

Парність.

Функція парна, якщо для будь-якого значення і із області визначення функції виконується рівність . Графік парної функції симетричний відносно осі

Функція непарна, якщо для будь-якого значення і із області визначення функції виконується рівність . Графік непарної функції симетричний відносно початку координат

Періодичність.

Функція періодична, якщо існує таке число (період функції), що для будь-якого з області визначення виконується рівність .

Якщо Т – період, то , де , також період функції.

Основні елементарні функції, їх властивості та графіки

1. Лінійна функція (рис.7).

область визначення: ;
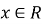графік 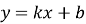є пряма лінія. Для побудови її достатньо двох точок, наприклад 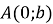і ,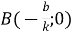

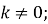
Рис. 7

кутовий коефіцієнт 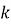характеризує кут, який утворює пряма 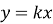з додатнім напрямом осі 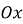: 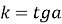. Якщо 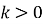– цей кут гострий, якщо 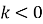– тупий;
при 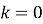, то графік функції 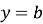є пряма, паралельна до осі .

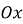2. Квадратична функція , (рис. 8).

область визначення: ;
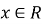графік функції є парабола. При 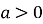вітки параболи направлені вгору, при 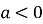– вниз. Вісь симетрії параболи – пряма ;
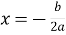координати вершини параболи визначаються за формулами
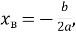
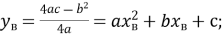
квадратичну функцію 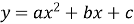завжди можна привести до вигляду 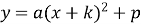шляхом виділення повного квадрату, де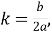 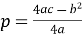. Точка А(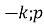) – вершина параболи;
графік квадратичної функції 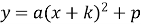одержується з графіка функції 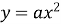за допомогою паралельного перенесення;
якщо 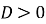, парабола перетинає вісь Ох у двох точках;
якщо 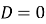, парабола дотикається до осі Ох;
якщо 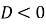, точок перетину з віссю Ох немає.

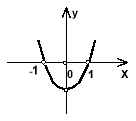
Рис. 8

Функція 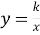, де 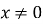(рис. 9).

змінна у обернено пропорційна х, 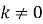– коефіцієнт оберненої пропорційності;
область визначення – множина всіх дійсних чисел, крім х=0;
графіком функції є гіпербола – крива, що складається з двох віток, симетричних відносно початку координат. Якщо 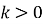, вітки розташовані в 1-й і 3-й чвертях, якщо 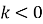, в 2-й і 4-й чвертях;
гіпербола 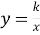не має точок перетину з осями координат.

Рис. 9

Степенева функція 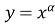, 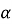– будь-яке дійсне число і показник степеня.

при цілих додатних 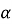функція визначена при :

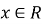– лінійна функція;

- парабола;

- кубічна парабола;

при раціональному 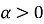графіки зображені на рисунках 10, 11, 12;
при ірраціональному 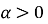степенева функція розглядається тільки при ;
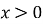при 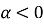лінії 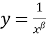, 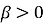називається гіперболами відповідних порядків (при 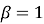– звичайна гіпербола (рис. 9), при 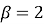(рис. 13);
лінії 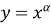у фізиці та техніці називають політропними кривими.

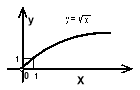
Рис. 10 Рис. 11

Рис. 12 Рис. 13

Показникова функція 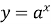, де 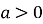, 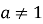(рис. 14).

область визначення: ;
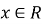множина значень ;
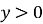якщ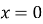о , то 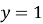при будь-якому а;
функція неперервна та диференційована в усій області визначення;
при 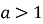функція монотонно зростає, при – монотонно спадає;
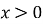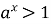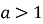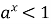якщо , то при , при ;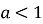
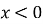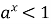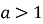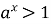якщо , то при , при ;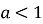
графік .

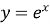Рис. 14

Логарифмічна функція 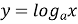, , 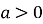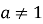(рис. 15).

логарифмічна функція є обернена до показникової;
область визначення ;
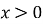множина значень функції y ;
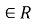функція неперервна та диференційована в усій області визначення;
функція монотонно зростає при 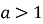і монотонно спадає при ;
при будь-якій основ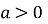і і 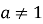мають місце рівності ;
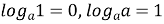якщо , то – десятковий логарифм;
якщо 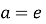(число Непера), то 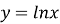– натуральний логарифм.

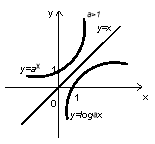
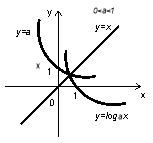
Рис. 15

Перетворення графіків функцій

Якщо відомий графік функції , то за допомогою деяких перетворень можна побудувати графіки більш складних функцій.

Графік функції 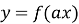одержується за допомогою стискання графіка 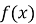в а разів до осі Оу, якщо 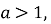або розтягу в раз, якщо

(рис. 16).

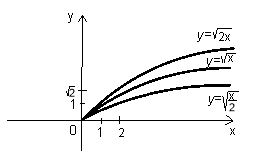
Рис. 16

Графік функції 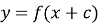одержується паралельним перенесенням графіка 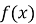вліво на с одиниць при 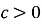та вправо на с одиниць при

с < 0 (рис. 17).

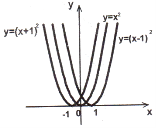
Рис. 17

Графік функції 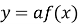одержується розтягом графіка 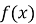уздовж осі Оу в а раз при 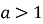і стисканням уздовж цієї ж осі в раз при (рис.18).

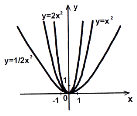
Рис. 18

Графік функції 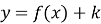одержується паралельним перенесенням графіка функції 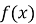вверх по осі Оу на k одиниць. Графік функції 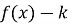паралельно переноситься вниз по осі Оу на k одиниць (рис. 19).

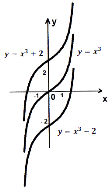
Рис. 19

Графік функції 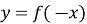одержується симетричним відображенням графіка 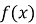відносно осі Оу (рис. 20).

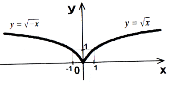
Рис. 20

Графік функції одержується симетричним відображенням графіка 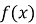відносно осі Ох (рис. 21).

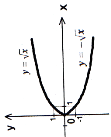
Рис. 21

Графік функції 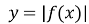одержується із графіка функції 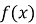наступним чином: частина графіка 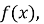яка лежить над віссю Ох, зберігається, та ж частина його, яка лежить під віссю Ох, відображається симетрично відносно осі Ох (рис. 22).

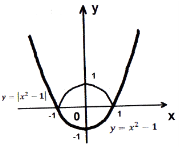
Рис. 22

Графік функції 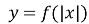одержується із графіка функції 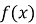наступним чином: при графік 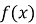зберігається, а при 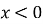одержана частина графіка відображається симетрично відносно осі Oy (рис. 23).

Рис. 23

Арифметична прогресія

Арифметична прогресія – послідовність чисел , у якій кожний наступний член утворюється з попереднього, додаванням одного і того ж числа d (різниці прогресії). При прогресія зростаюча, при – спадаюча.

Позначення: – перший член, – різниця, – кількість членів, – –й член, - сума перших n членів.

Загальний член арифметичної прогресії: .

Cума перших членів: .

Властивості арифметичної прогресії: , де , де .

Геометрична прогресія

Геометрична прогресія – послідовність чисел , в якій кожний наступний член утворюється з попереднього члена за допомогою множення на одне і те саме для даної послідовності число q.

Позначення: – перший член (), - знаменник геометричної прогресії (), – n-й член, - сума перших n членів.

Загальний член геометричної прогресії: .

Сума перших n членів: , де .

Властивості геометричної прогресії:

, де

Нескінченна спадна геометрична прогресія: , .

Сума обчислюється за формулою: .

Числові послідовності та їх суми

1) 1+2+3+…+ = ;

2) 1+2+5+…+()+ ()=;

3) 2+4+6+…+()+ =;

4) ;

5) ;

6) ;

7) .

Тригонометричні функції

Позначення: xOy – декартова прямокутна система координат.

R=AO – радіус кола з центром на початку координат; x, y – координати точки А; α – кут, який утворює радіус з додатним напрямом осі Оу

(рис. 24).

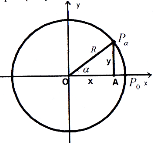
Рис. 24

Визначення тригонометричних функцій довільного кута:

; ; ; .

Секанс і косеканс α визначається такими формулами: , .

Значення тригонометричних функцій не залежить від довжини радіуса ОА, тому можна покласти R=1. Коло в цьому випадку називається одиничним колом і тригонометричні функції визначаються так: (ордината кінця радіуса); (абсциса кінця радіуса);

, .

Знаки тригонометричних функцій

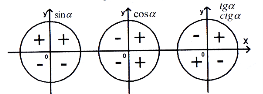
Рис. 25

Властивості та графіки тригонометричних функцій

Функція :

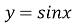область визначення: ;
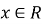множина значень: ;
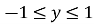функція періодична з основним періодом : ;
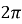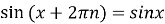функція непарна: ;
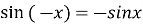нулі функції: 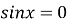, при , ;
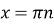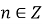функція зростає при і спадає при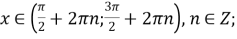
функція неперервна і має похідну при будь-якому ;
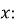
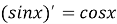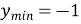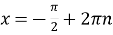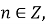
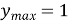екстремуми функції: при , при ,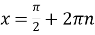

Графік функції називається синусоїдою (рис. 26).

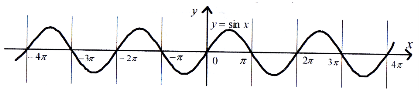
Рис. 26

Функція

область визначення: ;
множина значень: ;
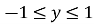функція періодична з основним періодом : ;
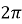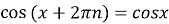функція парна: ;
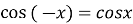нулі функції: 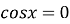, при
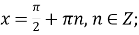
функція зростає при 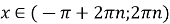і спадає при ;
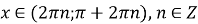функція неперервна і має похідну при будь-якому ;
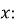
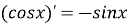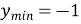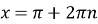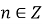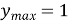екстремуми функції: при , , при ,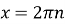

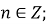
Графік функції називається косинусоїдою (рис. 27).

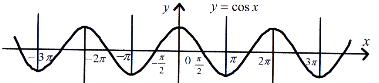
Рис. 27

Функція :

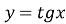область визначення: 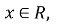крім , ;
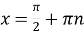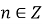множина значень: ;
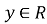функція періодична з основним періодом : ;
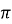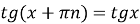функція непарна: ;
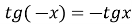нулі функції: 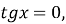при ;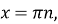
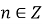функція зростає в кожному з проміжків ;
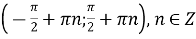функція неперервна і диференційована при будь-якому х із області визначення: ;

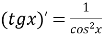Графік функції називається тангенсоїдою (рис. 28).

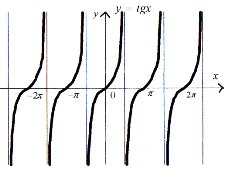
Рис. 28

Функція :

область визначення: 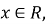крім ;
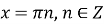множина значень: ;
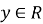функція періодична з основним періодом : ;
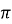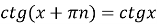функція непарна: ;
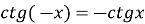нулі функції: 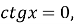при ;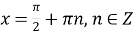
функція спадає в кожному з проміжків ;
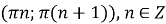функція неперервна і диференційована при будь-якому х із області визначення: ;

Графік функції називається котангенсоїдою (рис. 29).

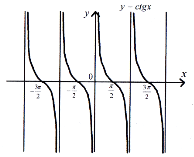
Рис. 29

Основні тотожності

Правила зведення

Щоб записати будь-яку формулу зведення, коли , слід пам’ятати правила:

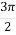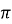Якщо формула містить кут або (, то функція змінюється на кофункцію (синус на косинус, тангент на котангенс і навпаки); якщо функція містить кут або 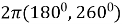, то найменування функції не змінюється.
Знак наступної частини прикладу визначається знаком попередньої частини прикладу.

Формули додавання

; ;
;

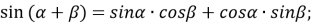
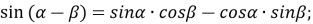
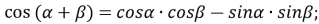
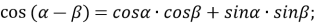
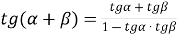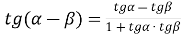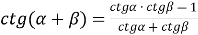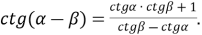
Формули подвійного і потрійного аргументів

;
;
;
;
;
;
.

Формули пониження степеня

;
;

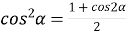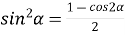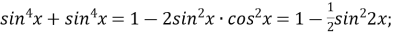
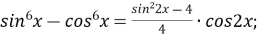
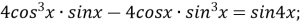
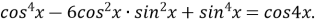
Формули половинного аргументу

; .

Формули перетворення суми та різниці в добуток

;

де ;

;
.

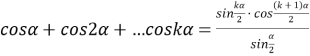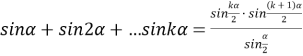Формули перетворення добутку в суму

; ;

;

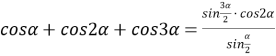Довільні формули перетворення

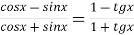; 2) .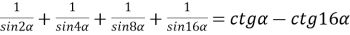

Властивості та графіки обернених тригонометричних функцій

, де ;

]; ];

); );

, де , де

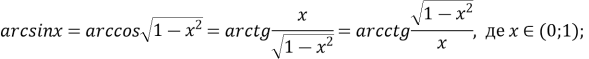
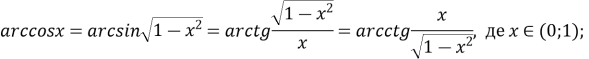
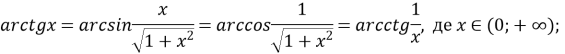
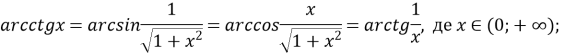
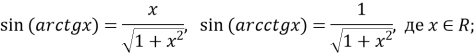
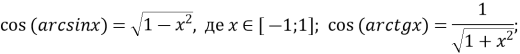
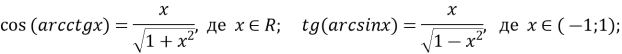
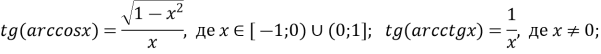
, де

де , де .

Обернені тригонометричні функції

Функція

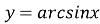
область визначення: ;
множина значень: ;
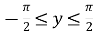функція непарна: ;
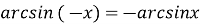нулі функції: 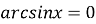при ;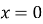
функція зростаюча.

Графік функції зображений на рис. 31.

Функція

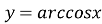
область визначення: ;
множина значень: ;
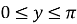функція непарна: ;
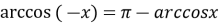нулі функції: 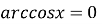при ;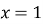
функція спадна.

Графік функції зображений на рис. 31.

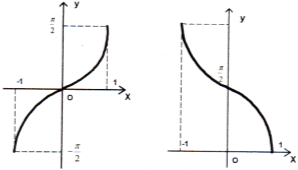
Рис. 30 Рис. 31

Функція

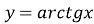
область визначення: ;
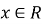множина значень: ;
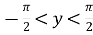функція непарна, ні непарна: ;
додатна при всіх х;
функція зростаюча.

Графік функції зображений на рис. 32.

Функція

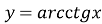
область визначення: ;

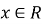множина значень: (0;;
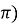функція ні парна, ні непарна, ;
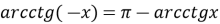спадає на всій області визначення;
;
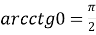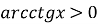для всіх ;
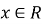неперервна і диференційована при всіх ;
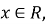
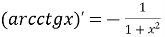графік функції 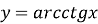дістаємо симетричним відображенням котангенсоїди, взятої на інтервалі (0;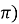, відносно прямої 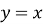(рис. 33).

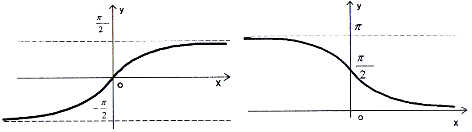
Рис. 32 Рис. 33

Найпростіші тригонометричні рівняння

Рівняння	Загальні випадки (n	Окремі випадки

	розв'язків немає
	+ 2
	розв'язків немає
	+
	+

Найпростіші тригонометричні нерівності

Вид нерівності	Множина розв'язків
()
()
()
()

Аксіоми планіметрії

I. Аксіоми належності точок і прямих на площині

1. Яка б не була пряма, існують точки, що належать цій прямій, і точки, які не належать їй.

2. Через будь-які дві точки можна провести пряму, і тільки одну.

II. Аксіоми вимірювання

1. Кожен відрізок має певну довжину, виражену додатнім числом.

2. Довжина відрізка дорівнює сумі довжин частин, на які розбивається відрізок будь-якою своєю точкою.

3. Кожен кут має певну величину (градусну міру), виражену додатнім числом.

4. Величина розгорнутого кута становить 180°.

5. Величина кута дорівнює сумі величин кутів, на які розбивається даний кут променем, що виходить з вершини даного кута і проходить між його сторонами.

III. Аксіоми відкладання

1. Яка б не була півпряма, на ній від її початку можна відкласти відрізок заданої довжини, і тільки один.

2. Яка б не була півпряма, від неї в задану півплощину можна відкласти кут із заданою градусною мірою, і тільки один.

IV. Аксіоми взаємного розташування точок на прямій і площині

1. Які б не були три точки прямої, одна і тільки одна з них розташована між двома іншими.

2. Пряма розбиває площину на дві півплощини.

3. Якщо на площині проведена пряма і кінці відрізка належать одній з півплощин, то цей відрізок не перетинає пряму.

4. Якщо на площині проведена пряма і кінці відрізка належать різним півплощинам, то цей відрізок перетинає пряму.

V. Аксіома паралельності

Через точку, що не належить прямій, можна провести пряму, паралельну даній, і тільки одну.

Аксіоми стереометрії

I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй.

Через будь-які дві точки можна провести пряму, й тільки одну.

II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими.

III. Кожний відрізок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.

IV. Пряма, що належить площині, розбиває цю площину на дві півплощини.

V. Кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут дорівнює . Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.

VI. На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини, й тільки один.

VII. Від півпрямої на площині, що містить її, можна відкласти в задану півплощину кут із даною градусною мірою, меншою за , і тільки один.

VIII. Який би не був трикутник, існує трикутник, що дорівнює йому, у даній площині в заданому розміщені відносно даної півпрямої у цій площині.

IX. На площині через дану точку, що не лежить на даній прямій, можна провести не більш як одну пряму, паралельну даній.

До цих аксіом додаються три аксіоми групи С.

. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй.

. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.

. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, й до того ж тільки одну.

Теорема 1. Через пряму і точку, яка не лежить на ній, можна провести площину, й до того ж тільки одну.

Теорема 2. Через пряму можна провести дві різні площини (див. рисунок).

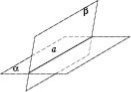
Теорема 3. Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

Отже, можливі три варіанти взаємного розміщення прямої і площини в просторі.

1. Пряма лежить у площині (рисунок зліва).

2. Пряма перетинає площину в даній точці (рисунок справа).

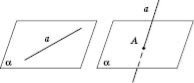
3. Пряма не перетинає площину (див. рисунок). У даному випадку пряма а називається паралельною площині.

Теорема 4. Через три точки, які не лежать на одній прямій, можна провести площину, й до того ж тільки одну.

Для розв’язання задач можуть бути корисними такі твердження.

1. Якщо дві різні прямі перетинаються у деякій точці (рисунок нижче зліва), то всі прямі, які перетинають обидві дані прямі й не проходять через цю точку, лежать в одній площині.

2. Усі прямі, які перетинають дану пряму й проходять через дану точку поза прямою, лежать в одній площині (рисунок справа).

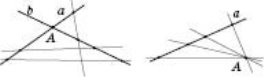
Кути

Промені АО і ОВ, які виходять з однієї точки О, утворюють кут: , де О – вершина кута, промені ОА і ОВ – сторони кута. Кути виміряються в градусах або в радіанах:

1 радіан радіана.

Властивості кутів (рис. 34, 35):

прямий кут дорівнює 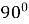, або радіан (його позначають буквою d);
гострий кут менший ;
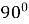тупий кут більший 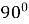, але менший ;
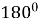суміжні кути мають одну спільну сторону, їх сума дорівнює 180⁰;
вертикальні кути рівні та утворюються перетином двох прямих;
внутрішні різносторонні кути ∠1=∠3, ∠2=∠4;
внутрішні односторонні кути ∠1+∠4=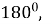∠2+.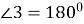

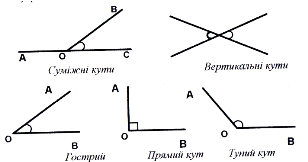
Рис. 34

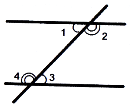
Рис. 35

Теорема Фалеса

Якщо паралельні прямі, які перетинають сторони кута, відтинають на одній його стороні рівні відрізки, то вони відтинають рівні відрізки і на другій його стороні (рис. 36).

Теорема про пропорційні відрізки

Паралельні прямі, які перетинають сторони кута, відтинають від сторін кута пропорційні відрізки (рис. 36).

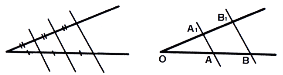
Рис. 36

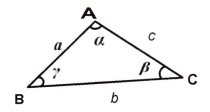
Трикутники

Позначення: - сторони; α, β, γ - кути.

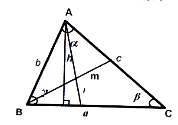
Гострокутний Прямокутний

Тупокутний

Рис. 37

півпериметр;

радіуси описаного та вписаного кіл відповідно;

висоти, проведені до сторін ;

відповідно бісектриса і медіана, проведені до сторони ;

площа трикутника.

Нехай с – найбільша сторона трикутника, тоді:

трикутник гострокутний;

трикутник прямокутний;

трикутник тупокутний (рис. 37).

Основні співвідношення між елементами трикутника

Властивості:

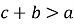, де а – найбільша із сторін;
α + β + γ =;
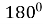теорема синусів ;
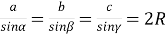теорема косинусів ;
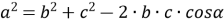середня лінія трикутника – відрізок, що сполучає середини двох сторін, паралельна третій стороні та дорівнює її половині.

Медіана трикутника

Медіана трикутника - відрізок, який сполучає вершину трикутника з серединою протилежної сторони (рис. 38).

Три медіани перетинаються в одній точці, що лежить всередині трикутника. Ця точка ділить кожну медіану у відношенні 2:1, якщо рахувати від вершини трикутника.

Точка перетину медіан є центром ваги трикутника або його центроїдом.

Медіана ділить трикутник на 2 рівновеликих трикутника ():

де медіана.

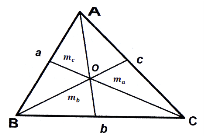
Рис. 38

Бісектриса трикутника

Бісектриса внутрішнього кута трикутника – відрізок, який ділить цей кут пополам. Три бісектриси перетинаються в одній точці.

Властивості:

бісектриса ділить протилежну сторону трикутника на відрізки, пропорційні двом прилеглим до неї сторонам: 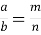(рис. 39);
бісектриса трикутника є геометричним місцем точок, рівновіддалених від сторін кута. Бісектриса CD ділить площу трикутника у відношенні, пропорційному прилеглим сторонам: ;
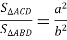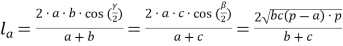, де 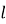- бісектриса;
(рис. 39);
центр вписаного кола – точка перетину бісектрис (рис. 40).

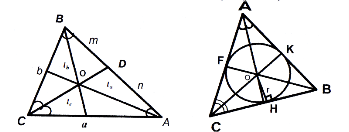
Рис. 39 Рис. 40

Висота трикутника

Висота трикутника – відрізок перпендикуляра, опущеного з вершини на протилежну сторону.

Властивості:

три висоти перетинаються в одній точці (ортоцентр трикутника), але ця точка не обов'язково лежить всередині трикутника (рис. 41):

, де 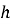- висота.

Центр описаного навколо трикутника кола лежить у точці перетину трьох серединних перпендикулярів, які проведені до сторін цього трикутника (рис. 42).

Якщо трикутник гострокутний, то центр описаного кола лежить всередині трикутника, в прямокутному – на середині гіпотенузи, а в тупокутному – зовні трикутника:

Рис. 41 Рис. 42

Ознаки рівності трикутників

Ознака рівності з двома сторонами та кутом між ними.

Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.

Ознака рівності за стороною та двома прилеглими кутами.

Якщо сторона та прилеглі до неї кути одного трикутника дорівнюють відповідно стороні та прилеглим до неї кутам другого трикутника, то такі трикутники рівні.

Ознака рівності за трьома ознаками.

Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні.

Ознаки подібності трикутників

Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники подібні: .
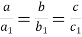Якщо два кути одного трикутника дорівнюють двом кутам другого трикутника, то такі трикутники подібні:
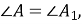
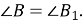
Якщо будь-які дві сторони одного трикутника пропорційні двом сторонам другого трикутника та кути між цими сторонами рівні, то такі трикутники подібні: .

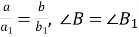Периметри подібних трикутників відносяться як їх відповідні лінійні розміри.

Площі подібних трикутників відносяться як квадрати їх відповідних розмірів, їх відношення дорівнює квадрату коефіцієнта подібності (рис. 43):

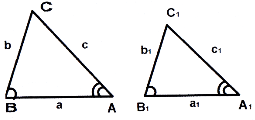
Рис. 43

Формули для обчислення площі трикутника

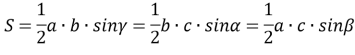
Правильний трикутник (a=b=c)

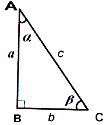
Прямокутний трикутник

Позначення:

проекції катетів a і b на гіпотенузу.

Властивості (рис. 45):

(відношення протилежного катета до гіпотенузи);
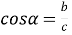(відношення прилеглого катета до гіпотенузи);
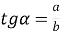(відношення протилежного катета до прилеглого);
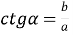(відношення прилеглого катета до протилежного);
теорема Піфагора: 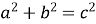, де 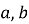- катети, с – гіпотенуза;
медіана, що виходить з вершини прямого кута прямокутного трикутника, дорівнює половині гіпотенузи;
;
; ;

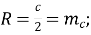
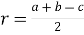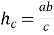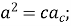
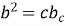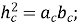
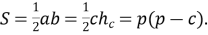
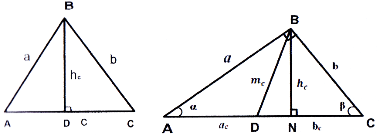
Рис. 44 Рис. 45

Рівнобедрений трикутник a = b

Позначення:

- центр вписаного кола, - центр описаного кола;

Властивості (рис. 46):

BD=DC; AD=; .

Рис. 46

Чотирикутники

Позначення:

і – діагоналі; ‒ кут між діагоналями; ‒ суміжні сторони; α ‒ кут між сторонами a і b; висота, опущена на сторону a; ‒півпериметр; ‒ площа.

Властивості (рис. 47):

у будь-якому опуклому чотирикутнику площа дорівнює ;
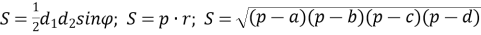сума внутрішніх кутів опуклого чотирикутника дорівнює ;
у чотирикутник можна вписати коло, якщо суми протилежних сторін рівні: ;
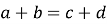сума діагоналей чотирикутника менша від його периметра;
навколо чотирикутника можна описати коло, якщо суми протилежних кутів рівні: ;
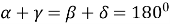якщо чотирикутник вписаний в коло, то: ;
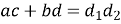середини сторін довільного чотирикутника є вершинами паралелограма.

Квадрат

Властивості (рис. 48):

периметр квадрата в чотири рази більше його сторін ;
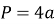всі кути квадрата рівні і дорівнюють ;
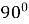діагоналі перетинаються під прямим кутом. Діагоналі квадрата в 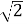разів більше його сторони ;
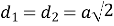навколо будь-якого квадрата можна описати коло. В будь-який квадрат можна вписати коло ;
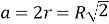площа квадрата дорівнює .

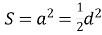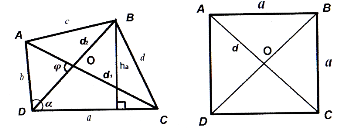
Рис. 47 Рис. 48

Прямокутник

Властивості (рис.49):

протилежні сторони рівні 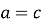, 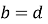та всі кути прямі;
діагоналі прямокутника рівні. Квадрат діагоналі прямокутника дорівнює сумі квадратів двох сусідніх сторін: ;
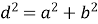навколо будь-якого прямокутника можна описати коло: ;
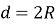периметр дорівнює: ;
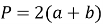при перетині бісектрис внутрішніх кутів довільного паралелограма утворюється прямокутник;
середини сторін прямокутника є вершинами ромба;
площа прямокутника дорівнює: .

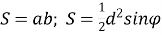Паралелограм

Властивості (рис. 50):

;
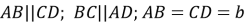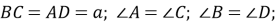
∠A+∠B=∠B+∠C=;
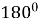діагоналі точкою перетину діляться навпіл ;
; ;
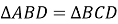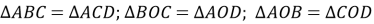сума квадратів сторін дорівнює сумі квадратів діагоналей: ;
.

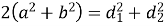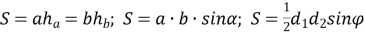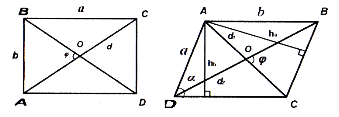
Рис. 49 Рис. 50

Ромб

Властивості (рис. 51):

усі сторони ромба рівні, протилежні кути рівні;
діагоналі ромба перпендикулярні ;
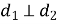сума квадратів діагоналей дорівнює сумі квадратів сторін ;
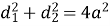площа ромба дорівнює: ;
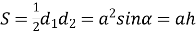середини сторін ромба є вершинами прямокутника;
у будь-який ромб можна вписати коло, центр вписаного кола радіуса 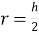лежить у точці перетину діагоналей.

Трапеція

Позначення:

а – менша основа, b - більша основа, - висота, - середня лінія, .

Властивості (рис. 52):

1) ;

2) ;

3) навколо трапеції можна описати коло тільки тоді, коли вона рівнобічна;

4) якщо в трапецію можна вписати коло, то суми протилежних сторін рівні;

Рис. 51

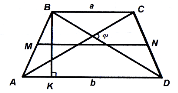
Рис. 52

5) у рівнобічній трапеції проекція діагоналей на більшу основу дорівнює середній лінії;

якщо трапеція вписана в коло, то вона рівнобічна, а сума її внутрішніх протилежних кутів дорівнює ;
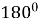якщо в рівнобічну трапецію вписати коло, то її бічна сторона дорівнює середній лінії;
середня лінія трапеції ділить пополам будь-який відрізок, кінці якого лежать на основах;
якщо в рівнобічній трапеції діагоналі взаємно перпендикулярні, то висота її дорівнює середній лінії;
якщо діагоналі рівнобічної трапеції є бісектрисами гострих кутів, то її бічна сторона дорівнює меншій основі;
якщо діагоналі рівнобічної трапеції є бісектрисами тупих кутів, то її бічна сторона дорівнює більшій основі;
площа рівнобічної трапеції, діагоналі якої взаємно перпендикулярні, дорівнює квадрату її висоти і ;
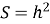висота рівнобічної трапеції, в яку можна вписати коло, є середнім геометричним її основ ;
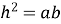радіус кола, описаного навколо трапеції, дорівнює радіусу кола, описаного навколо трикутника, вершини якого лежать у вершинах трапеції;
середини сторін рівнобічної трапеції є вершинами ромба.

Многокутник

Многокутник опуклий, якщо при продовженні будь-якої з його сторін увесь многокутник лежить по одну сторону від цієї прямої.

Діагональ многокутника – відрізок, що з'єднує дві не сусідні вершини.

Число діагоналей опуклого - кутника дорівнює .

Сума внутрішніх кутів опуклого - кутника дорівнює .

Сума зовнішніх кутів опуклого – кутника, якщо взяти по одному при кожній вершині, дорівнює .

Правильний многокутник

Позначення: - сторона; - радіус описаного кола, - радіус вписаного кола, S - площа (рис. 53).

;

Довжина сторони:

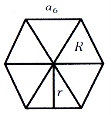
Рис. 53

Подібні многокутники

Якщо сторони одного многокутника пропорційні сторонам другого многокутника і відповідні кути цих многокутників рівні, то такі многокутники подібні.

Периметри подібних многокутників відносяться як їх відповідні сторони.

Площі подібних многокутників відносяться як квадрати відповідних сторін.

Коло та круг

Позначення: – радіус, L – довжина кола, S - площа круга, l - довжина дуги, a - хорда, що стягує дугу, α - центральний кут в радіанах, що стягує хорду, – градусна міра кута.

Сектор круга – частина круга, обмежена двома його радіусами (рис. 55).

Сегмент круга – частина круга, обмежена хордою і дугою, що її стягує (рис. 56).

Дотична до кола – пряма, яка має з колом тільки одну спільну точку.

Січна – пряма, яка має з колом дві спільні точки (CN).

;

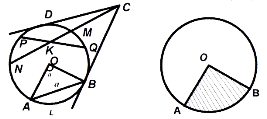
Рис. 54 Рис. 55

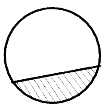
Рис. 56

Властивості хорд, дотичних і січних

Властивості:

діаметр, який ділить хорду пополам, перпендикулярний до цієї хорди;
рівні хорди рівновіддалені від центру;
рівні дуги стягуються рівними хордами;
між відрізками хорд, що перетинаються, має місце співвідношення: ;
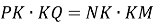дотична перпендикулярна до радіуса кола і проходить через його кінець: ;
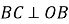через точку, що лежить поза кругом, можна провести дві рівні дотичні: CD=CB;
якщо через точку, що лежить поза кругом, провести дотичну (CD) і січну (CN), то відрізки дотичної і січної зв'язані співвідношенням:

Кути в колі

Центральний кут – кут з вершиною в центрі кола ∠BOC.

Вписаний у коло кут – це кут, вершина якого належить колу, а сторони перетинають коло.

Описаний кут – кут, утворений двома дотичними до кола, що проходять через одну точку поза колом (∠BAC) (рис. 58).

Властивості (рис. 57):

величина центрального кута дорівнює кутовій величині дуги, на яку він спирається: ∠AOB=;
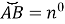величина вписаного кута дорівнює половині кутової величини дуги, на яку він спирається (вписаний кут вимірюється половиною центрального кута, якщо вони спираються на рівні дуги) ;
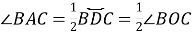величина описаного кута дорівнює піврізниці кутових величин дуг, які заключні між його сторонами: ∠BAC=.

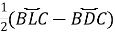Рис.57 Рис. 58

Властивості ліній в колах, які дотикаються і перетинаються

Лінія центрів двох кіл, які дотикаються, проходять через точки дотику.

Спільна внутрішня дотична двох кіл, які зовні дотикаються одне до одного, перпендикулярна до лінії їх центрів.

Спільна дотична двох кіл, які дотикаються внутрішньо, перпендикулярна до лінії їх центрів.

Спільна хорда двох кіл, які перетинаються, перпендикулярна до лінії двох центрів і ділиться цією лінією навпіл.

Взаємне розміщення двох прямих у просторі

Дві прямі, що перетинаються – це дві прямі, що мають лише одну спільну точку.
Паралельні прямі – дві прямі, що лежать в одній площині й не мають спільних точок.
Мимобіжні прямі – дві прямі, що лежать в одній площині та не перетинаються.

Взаємне розміщення прямої і площини в просторі

Пряма, що перетинає площину - це пряма, яка має тільки одну спільну точку з площиною.
Пряма, паралельна площині – це пряма, яка не має спільних точок з площиною.
Пряма, що лежить у площині – це пряма, кожна точка якої належить площині.

Взаємне розміщення двох площин у просторі

Дві площини перетинаються – дві різні площини, що мають спільні точки (рис. 59).
Паралельні площини – площини, які не мають спільних точок (рис. 60).

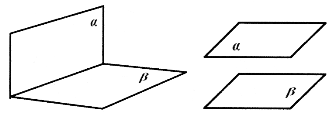
Рис. 59 Рис. 60

Перпендикулярність прямої і площини

Пряма, яка перетинає площину, називається перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить у цій площині й проходить через точку перетину (рис. 61).
Якщо пряма перпендикулярна двом прямим, які лежать у деякій площині і перетинаються, то вона перпендикулярна даній площині (рис. 62).

Перпендикуляр і похила. Теорема про три перпендикуляри

Перпендикуляр, опущений з даної точки на площину, - відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площині (рис.63).

Кінець цього відрізка, який лежить у площині, є основа перпендикулярна. Похила, проведена з даної точки до площини, - будь-який відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром до площини. Кінець відрізка, що лежить у площині, називають основою похилої. Відрізок, що сполучає основи перпендикуляра і похилої, проведених з однієї й тієї самої точки, називають проекцією похилої.

Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої. І навпаки:

якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої (рис. 64).

АО – перпендикуляр до площини , АВ – похила до площини , ВО – проекція похилої АВ на площину .

Рис. 63 Рис. 64

Перпендикулярність двох площин

Перпендикулярні площини – дві площини, що перетинаються, за умови, якщо третя площина, перпендикулярна до лінії їх перетину, перетинає їх по перпендикулярних прямих (рис. 65).
Якщо пряма, що лежить в одній площині, перпендикулярна другій площині, то ці площини перпендикулярні (рис. 66).

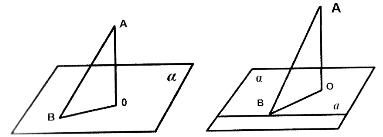
Рис. 65 Рис. 66

Двогранні кути. Тригранні кути

Двогранний кут – фігура, утворена двома півплощинами зі спільною прямою, що їх обмежує (рис. 67). Півплощини називають гранями, а пряму, що їх обмежує (рис. 67). Півплощини називають гранями, а пряму, що їх обмежує, - ребром двогранного кута, α і β – грані двогранного кута, а – його ребро.

Лінійний кут двогранного кута – кут, який є перерізом цього двогранного кута і площини, яка перпендикулярна ребру (рис. 68).

Міра двогранного кута – міра відповідного йому лінійного кута, знаходиться в межах від 0⁰ до 180⁰.

Тригранний кут SABC – фігура, яка складається з трьох плоских кутів ASB, BSC, ASC. Вершина тригранного кута – S; AS, BS, SC – плоскі кути тригранного кута, тобто грані тригранного кута (рис. 69).

Двогранні кути, утворені гранями тригранного кута, називають двогранними кутами тригранного кута.

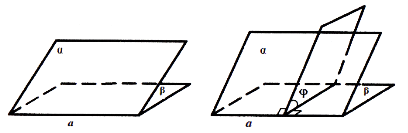
Рис. 67 Рис. 68

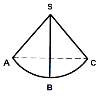
Рис. 69

Призма

Призмою називається многогранник, який складається з двох плоских многокутників, які лежать у різних площинах і суміщаються паралельним перенесенням, та всіх відрізків, що сполучають відповідні точки цих многокутників.

Призма – кутна має: грані, ребер, вершин.

У - кутної призми діагоналей (n>3).

Діагональний переріз призми – паралелограм.

Пряма призма – призма, всі бічні ребра якої перпендикулярні основам (рис. 71). У протилежному випадку призма називається похилою (рис. 72).

Висота призми – відрізок перпендикуляра до площин основ призми, кінці якого належать цим площинам.

Бічні грані прямої призми – прямокутники.

Бічне ребро дорівнює висоті прямої призми.

Усі двогранні кути при ребрах основи прямої призми прямі.

Діагональний переріз прямої призми – прямокутник.

Правильна призма – пряма призма, основою якої є правильний многокутник. Правильна призма має всі властивості призми і прямої призми.

Бічні грані правильної призми рівні.

Двогранні кути при бічних ребрах рівні. Лінійні кути цих двогранних кутів дорівнюють: .

Позначення:

бічне ребро, P ‒ периметр основи, ‒ площа основи, H ‒ висота, ‒ периметр перпендикулярного перерізу, ‒ площа бічної поверхні,

V ‒ об'єм, ‒ площа повної поверхні призми.

У прямої призми .

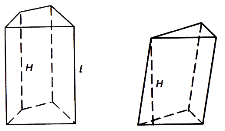
Рис. 71 Рис. 72

Паралелепіпед

Позначення: - виміри, - діагональ прямокутного паралелепіпеда.

Паралелепіпед – призма, основами якої є паралелепіпед. Усі шість граней паралелепіпеда – паралелограми.

Діагоналі паралелепіпеда – відрізки, які сполучають вершини паралелепіпеда, що не належать одній і тій же грані.

Паралелепіпед, бічні ребра якого перпендикулярні до площини основи, називається прямим (рис. 74).

Усі бічні грані прямого паралелепіпеда – прямокутника. Бічні грані перпендикулярні основам.

Прямий паралелепіпед, основою якого є прямокутник, називається прямокутним (рис. 75).

Куб прямокутний паралелепіпед – з рівними вимірами, тобто .

Усі шість граней куба – рівні квадрати (рис. 73).

Якщо – ребро куба, - діагональ, то .

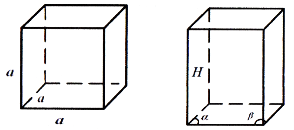
Рис. 73 Рис. 74

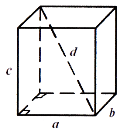
Рис. 75

Піраміда

Позначення:

- периметр основи, l - апофема, H - висота, - площа основи, - площа бічної поверхні, - площа повної поверхні, V - об'єм.

Пірамідою називається многогранник, який складається з плоского многокутника – основи піраміди, точки, яка не лежить у площині основи, - вершини піраміди і всіх відрізків, що сполучають вершину піраміди з точками основи.

Многокутник називається основою піраміди, грані (трикутники) – бічні грані. Спільна вершина всіх бічних граней називається вершиною піраміди.

Висота піраміди – відрізок перпендикуляра, проведеного з вершини до площини основи.

Піраміда правильна, якщо основа її є правильний многокутник, а проекція вершини на площину основи збігається з центром цього многокутника (рис. 76).

Усі бічні ребра правильної піраміди рівні між собою, всі бічні грані – рівні рівнобедрені трикутники. У правильної піраміди всі плоскі кути при вершині рівні.

Висота бічної грані правильної піраміди, яка проведена з її вершини, називається апофемою піраміди. Апофеми правильної піраміди рівні.

Для будь-якої піраміди: .

Для правильної піраміди: .

Якщо в трикутній піраміді усі бічні ребра утворюють рівні кути з площиною основи, то вершина піраміди проектується в центр кола, описаного навколо трикутника в основі (рис. 77).

Якщо в трикутній піраміді усі бічні грані утворюють рівні кути з площиною основи, то вершина піраміди проектується в центр кола, вписаного в трикутник, що лежить в основі (рис. 78).

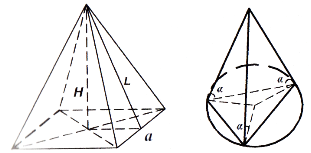
Рис. 76 Рис. 77

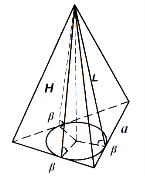
Рис. 78

Зрізана піраміда

Позначення: ₁, ₂‒ периметри основ, l ‒ апофема, H ‒ висота, ₁, ₂‒ площі основ, V ‒ об'єм, _біч‒ площа бічної поверхні правильної зрізаної піраміди.

Якщо через точку, що належить будь-якому бічному ребру піраміди, провести площину, паралельну площині основи, то многогранник, вершинами якого є вершини основи піраміди і вершини основи піраміди, що відрізається, називається зрізаною пірамідою. Бічні грані зрізаної піраміди – трапеції.

Зрізана піраміда правильна, якщо вона – частина правильної піраміди. Бічні грані правильної зрізаної піраміди – рівні рівнобічні трапеції; висота цих трапецій називається апофемою зрізаної піраміди (рис. 79).

Циліндр

Позначення: ‒ радіус основи, H ‒ висота, V ‒ об'єм, _біч ‒ площа бічної поверхні, _пов ‒ площа повної поверхні.

Циліндром називається тіло, що складається з двох кругів, які не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих кругів (рис. 80).

Основи циліндра рівні і паралельні. Твірні циліндра рівні і паралельні. Висота циліндра дорівнює твірній.

Переріз циліндра площиною, яка паралельна осі, або осьовий переріз – прямокутник.

, , .

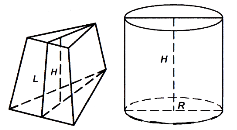
Рис. 79 Рис. 80

Конус

Позначення:

‒ радіус основи, ‒ висота, площа основи, площа бічної поверхні, площа повної поверхні, об'єм.

Конусом називається тіло, яке складається з круга – основи конуса, точки, яка не лежить у площині цього круга – вершини конуса і всіх відрізків, що сполучають вершину конуса з точками основи (рис. 81). Розгортка бічної поверхні конуса є круговим сектором.

, , , =

Зрізаний конус

Позначення:

₁, ₂‒ радіуси нижньої і верхньої основ, H ‒ висота, L ‒ твірна, V ‒ об'єм, площа бічної поверхні. Зрізаний конус – частина конуса, яка обмежена його основою і перерізом, паралельним площині основи (рис. 82).

Осьовий переріз зрізаного конуса – рівнобічна трапеція.

Твірні зрізаного конуса утворюють рівні кути з основою.

Куля і сфера

Куля – множина всіх точок простору, які знаходяться від даної точки (центра) на відстані, не більше R (радіус кулі), (рис. 83).

Сфера – поверхня кулі.

Кульовий сектор – фігура, яка утворена при обертанні кругового сектора АОК навколо радіуса ОК.

Кульовий сегмент – фігура, яка одержується при обертанні кругового сегменту АКВ навколо радіуса ОК, перпендикулярного до його хорди АВ, Н=КМ – висота сегменту.

Об'єм кулі: .

Площа сфери: .

Об'єм кульового сегменту: .

Площа сегментної поверхні: .

Об'єм кульового сектора: .

Площа повної поверхні кульового сектора:

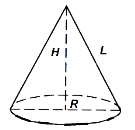
Рис. 81

Рис. 82 Рис. 83

Декартові координати на площині

Нехай і – дві точки на площині хОу (рис. 84).

Відстань d між ними визначається за формулою:

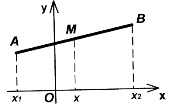
Рис. 84

Якщо точка M ділить відрізок АВ у відношенні , то її координати дорівнюють: , , .

Якщо при цьому , тобто М – середина відрізка АВ, то:

, , .

Коло на площині

Рівняння кола з центром у точці і радіусом має вигляд:

Якщо центр кола у початку координат, то його рівняння набуває вигляду:

Пряма на площині

Загальне рівняння прямої: , де .

Положення прямої в окремих випадках:

1) , тоді – пряма, паралельна осі Ох (рис. 85).

2) , – по аналогії пряма, паралельна осі Оу, і збігається з нею, якщо (рис. 86);

3) , тоді – пряма проходить через т. О (0;0) (рис. 87).

Рівняння прямої з кутовим коефіцієнтом .

Кутовий коефіцієнт з точністю до знаку дорівнює тангенсу гострого кута, який утворює пряма з віссю Ох.

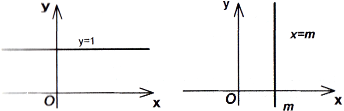
Рис. 85 Рис. 86

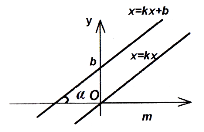
Рис. 87

Декартові координати у просторі

Нехай A і B – дві точки у просторі. Відстань між ними визначається за формулою:

Площина в просторі

Загальне рівняння площини .

Коефіцієнти a, b і c у цьому рівнянні є координати вектора, перпендикулярного цій площині:

Якщо точка належить площині, то рівняння площини набуває вигляду (рис. 88): .

Пряма лінія у просторі задається рівнянням двох площин, що проходять через цю пряму (рис. 89):

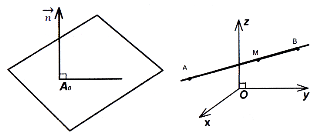
Рис. 88 Рис. 89

Вектори

Вектор – це направлений відрізок (рис. 90).

Позначення вектора: або , А ‒ початок, В ‒ кінець вектора.

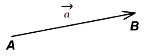
Рис. 90

Модуль (абсолютна величина) вектора – довжина відрізка, що зображає вектор, позначається .

Якщо початок вектора збігається з його кінцем, то вектор називається нульовим вектором.

Два вектори називаються рівними, якщо їх відповідні координати рівні.

Два вектори колінеарні, якщо вони лежать на одній або паралельних прямих.

Лінійні операції над векторами

Правило трикутника (рис. 91).

Сума векторів є вектор , який сполучає початок вектора і кінець вектора .

Правило паралелограма (рис. 92).

Якщо вектори і зведені до спільного початку і на них побудований паралелограм, то сума є вектор, який збігається з діагоналлю цього паралелограма і виходить з їх спільного початку.

Різниця 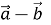двох векторів є вектор 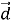, який в сумі з вектором 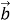складає вектор 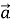(рис. 93).

Якщо вектори і зведені до спільного початку, то різниця є вектор, який іде з кінця вектора в кінець вектора .

Правило многокутника (рис. 94).

Якщо треба знайти суму кількох векторів, можна скористатися правилом многокутника.

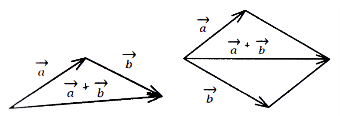
Рис. 91 Рис. 92

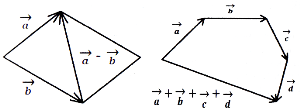
Рис. 93 Рис. 94

Добуток вектора на число (скаляр) 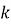є вектор, модуль якого дорівнює .

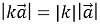Направлення вектора (при ) збігається з направленням вектора , якщо k>0, і протилежне до направлення вектора , якщо k<0.

Для будь-яких трьох векторів ), ) i ), справедлива рівність .

Координати вектора

Координати вектора з початком у т. і кінцем у т. називається вектор

Модуль вектора знаходиться за формулою: .

Сумою векторів ) і ) називається вектор

Різницею є вектор

Добутком вектора на число k є вектор ) .

Умова колінеарності векторів і – пропорційність відповідних координат: .

Скалярний добуток векторів

Скалярний добуток векторів дорівнює добутку їх модулів на косинус між ними .

Скалярним добутком векторів ) і ) називається число .

Кут між векторами .

Умова перпендикулярності векторів – рівність нулю скалярного добутку: або

Скалярний квадрат вектора: .

Якщо вектор лежить у площині хОу, то він має тільки дві координати . Відповідний вигляд приймуть усі вище зазначені формули.

Комбінаторика та біном Ньютона

Скінченна множина впорядкована, якщо кожному її елементу присвоєний свій порядковий номер.

Будь-який встановлений у скінченній множині порядок елементів називається перестановкою елементів множини.

Число перестановок із елементів знаходиться за формулою:

Нехай множина М має елементів. Кожну її впорядковану – елементну підмножину називають розміщенням із елементів по .

Число розміщень із елементів по знаходиться за формулою .

Кожну – елементну підмножину множини М називають комбінацією із елементів по .

Число комбінацій із елементів по знаходиться за формулою: .

Справедливі такі властивості комбінацій: , ,

Формула бінома Ньютона

+ або +

Окремі випадки:

;
;
;
;
.

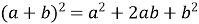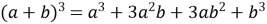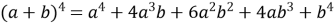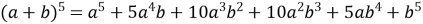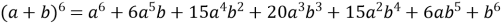Поняття похідної

Похідною функції у точці називається границя , де - приріст аргументу в точці .

Якщо ця границя існує, то кажуть, що функція диференційована в точці . Похідну позначають: =.

Для існування диференціала необхідно і достатньо, щоб існувала похідна , причому .

Правила диференціювання

Якщо с – стала величина і функції – диференційовані в точці , то справедливі формули:

1) ;

2) ;

3) ;

4) .

Похідна складеної функції

Нехай і – складна функція. Якщо диференційована в точці і диференційована в точці , то похідна складної функції в т. дорівнює:

Похідні основних елементарних функцій

1) а) , б) ; в) ;

2) ;

3) ;

4) ;

5) ;

6) а) , б) ;

7) а) б) ;

8) ;

9) ;

8) ;

9) .

Геометричний зміст похідної

Похідна функції у точці дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції в точці .

Рівняння дотичної має вигляд: (рис. 95).

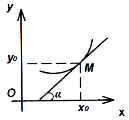
Рис. 95

Фізичний зміст похідної

Якщо – закон руху точки, то швидкість у момент часу визначається співвідношенням: , де миттєва швидкість .

Невизначений інтеграл

Функція – первісна функції на проміжку Х (скінченному або нескінченному), якщо для всіх х з цього проміжку .

Невизначений інтеграл від функції на проміжку – сукупність усіх її первісних: , де .

Основні властивості невизначеного інтегралу

4) (замінна змінної).

Основні формули інтегрування

1) , де

2) ;

3) +C;

4) +C;

10) а) ; b) ;

11)

Визначений інтеграл

Формула Ньютона-Лейбніца: де – первісна функції .

Властивості визначеного інтегралу

6) якщо на , то ;

7) якщо і найменше і найбільше значення функції на

Геометричний зміст визначеного інтегралу

якщо функція 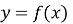невід'ємна і неперервна на 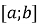, то площа криволінійної трапеції (рис. 96) обчислюється за формулою: ;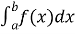
якщо, обмежена двома неперервними кривими 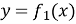і 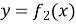, причому 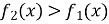, та двома прямими 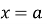і 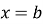(рис. 97, 98), дорівнює: ;
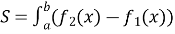якщо функція 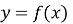від'ємна і неперервна на 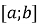, то площа криволінійної трапеції (рис. 99) обчислюється за формулою: ;
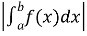площа, обмежена двома неперервними кривими 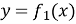і 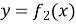, та двома прямими 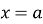і 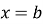(рис. 100), дорівнює: ;
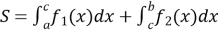якщо функція 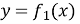від'ємна, а функція 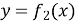додатна, тоді площа дорівнює: 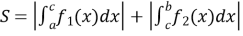, (рис. 101);
якщо функці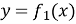ї і 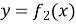від'ємні, тоді: 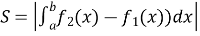, (рис. 102).

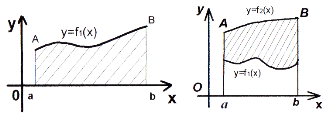
Рис. 96 Рис. 97

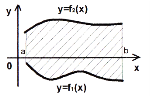
Рис. 98

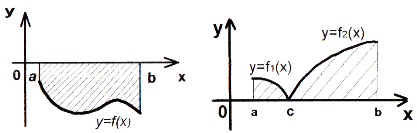
Рис. 99 Рис. 100

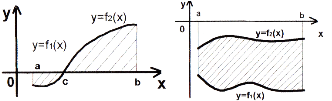
Рис. 101 Рис. 102

Таблиці квадратів двозначних чисел

Десятки	Одиниці
	1	2	3	4	5	6	7	8	9
1	121	144	169	196	225	256	289	324	361
2	441	484	529	576	625	676	729	784	841
3	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	5041	5184	5329	5476	5625	5776	5819	6084	6241
8	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8281	8464	8649	8836	9025	9216	9409	9604	9801

Таблиця простих чисел

2	3	5	7	11	13	17	19	23	29
31	37	41	43	47	53	59	61	67	71
73	79	83	89	97	101	103	107	109	113
127	131	137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223	227	229
233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541
547	557	563	569	571	577	587	593	599	601
607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733
739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863
877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997

Обернені числа, квадрати, куби, корені

n
0	не існує	0	0	0	0
1	1	1	1	1	1
2	0,5	4	8	1,4	1,26
3	0,33	9	27	0,73	0,44
4	0,25	16	64	2	1,59
5	0,2	25	125	2,24	1,71
6	0,17	36	216	2,45	1,82
7	0,14	49	343	2,65	1,91
8	0,13	64	512	2,83	2
9	0,11	81	729	3	2,08
10	0,1	100	1000	3,16	2,15

Таблиця тригонометричних функцій деяких функцій

α	,
	0
	0			1		0	-1
	1			0		-1	0
	0		1	-	-1	0	-
	-	1	1	0	-1	-	0

Співвідношення

між одиницями

довжини

Співвідношення

між одиницями

площі

Співвідношення

між одиницями

об'єму

Співвідношення

між одиницями

маси

1 см = 10 мм

1дм = 10 см

1 м = 10 дм

1 дм = 100 мм

1 м = 100 см

1 м = 1000 мм

1 км = 1000 м

1 км = 100000 см

1см² = 100 мм²

1 дм² = 100 см²

1 м² = 100 дм²

1 а = 100 м²

1 га = 100 а

1 км² = 1000000 м²

1 см³= 1000 мм³

1 дм³ = 1000 см³

1 м³ = 1000 дм³

1 кг = 1000 г

1 ц = 100 кг = 100000 г

1 т = 10 ц = 1000 кг

1 т = 1000000 г

Деякі степені чисел 2, 3, 5

128

256

512

1024

2048

4096

8192

16384

32768

65536

131072

262144

524288

1048576

243

729

2187

6561

19683

59049

177147

531441

1594323

4782969

14348907

43046721

129140163

387420489

1162261467

3486784401

125

625

3125

15625

78125

390625

1953125

9765625

48828125

244140625

1220703125

6103515625

30517578125

152587890625

762939453125

3814697265625

19073486328125

95367431640625

docx

Завантажити

Зберегти на потім

Додав(-ла)

Мірошніченко Ганна Іванівна

Пов’язані теми

Алгебра, Методичні рекомендації

Додано

10 лютого 2020

Переглядів

1323

Оцінка розробки

Відгуки відсутні

2	3	5	7	11	13	17	19	23	29
31	37	41	43	47	53	59	61	67	71
73	79	83	89	97	101	103	107	109	113
127	131	137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223	227	229
233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541
547	557	563	569	571	577	587	593	599	601
607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733
739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863
877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997

2	3	5	7	11	13	17	19	23	29
31	37	41	43	47	53	59	61	67	71
73	79	83	89	97	101	103	107	109	113
127	131	137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223	227	229
233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541
547	557	563	569	571	577	587	593	599	601
607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733
739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863
877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997

2	3	5	7	11	13	17	19	23	29
31	37	41	43	47	53	59	61	67	71
73	79	83	89	97	101	103	107	109	113
127	131	137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223	227	229
233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541
547	557	563	569	571	577	587	593	599	601
607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733
739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863
877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997