Довжина вектора у просторі

Про матеріал

Дидактичні матеріали у нетрадиційній формі зручно використовувати на уроках та індивідуальних заняттях при вивченні нових тем. Кожна розробка містить: - бланк завдань на 11-12 прикладів, що є зручним для оцінювання. Завдання підібрані з поступовим збільшенням рівня складності. - бланк відповідей. - історична довідка про походження та використання у різних галузях закодованого математичного терміну.

Перегляд файлу

10 клас

Тема: Довжина вектора.

Мета: Формування умінь та навичок учнів застосовувати формули для знаходження координат вектора та довжини вектора у просторі.

Завдання:

Обчисліть довжини векторів:

Дано:	Розв'язування:
О ( -1; 0; -6)	1) \|ОА\| =
Р ( 7 ; 4 ; -5)	2) \|ОР\| =
А ( 5 ; -2 ; 3)	3) \|АД\| =
В ( 1 ; -2; 0)	4) \|ВС\| =
С ( 6 ; 10; 0)	5) \|ДК\| =
Д ( 5; 4; 11)	6) \|АК\| =
К ( -4; 4; -1)	7) \|АВ\| =
М ( 1; 1; 3)	8) \|ВД\| =
Знайти:	9) \|АМ\| =
	10) \|СД\| =
	11) \|АС\| =

Шифратор

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

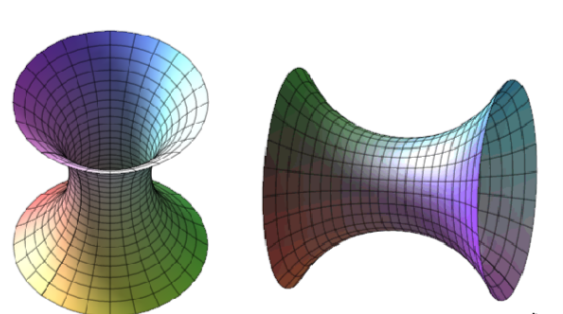
Термін "гіперболоїд" (грец. від hyperbole — гіпербола, і eidos — подібність).

Прикладами гіперболоїдних конструкцій є:

Дано:	Розв'язування:	Дано:	Розв'язування:
О ( -1; 0; -6)	1) \|ОА\| =	О ( -1; 0; -6)	1) \|ОА\| =
Р ( 7 ; 4 ; -5)	2) \|ОР\| =	Р ( 7 ; 4 ; -5)	2) \|ОР\| =
А ( 5 ; -2 ; 3)	3) \|АД\| =	А ( 5 ; -2 ; 3)	3) \|АД\| =
В ( 1 ; -2; 0)	4) \|ВС\| =	В ( 1 ; -2; 0)	4) \|ВС\| =
С ( 6 ; 10; 0)	5) \|ДК\| =	С ( 6 ; 10; 0)	5) \|ДК\| =
Д ( 5; 4; 11)	6) \|АК\| =	Д ( 5; 4; 11)	6) \|АК\| =
К ( -4; 4; -1)	7) \|АВ\| =	К ( -4; 4; -1)	7) \|АВ\| =
М ( 1; 1; 3)	8) \|ВД\| =	М ( 1; 1; 3)	8) \|ВД\| =
Знайти:	9) \|АМ\| =	Знайти:	9) \|АМ\| =
	10) \|СД\| =		10) \|СД\| =
	11) \|АС\| =		11) \|АС\| =
Дано:	Розв'язування:	Дано:	Розв'язування:
О ( -1; 0; -6)	1) \|ОА\| =	О ( -1; 0; -6)	1) \|ОА\| =
Р ( 7 ; 4 ; -5)	2) \|ОР\| =	Р ( 7 ; 4 ; -5)	2) \|ОР\| =
А ( 5 ; -2 ; 3)	3) \|АД\| =	А ( 5 ; -2 ; 3)	3) \|АД\| =
В ( 1 ; -2; 0)	4) \|ВС\| =	В ( 1 ; -2; 0)	4) \|ВС\| =
С ( 6 ; 10; 0)	5) \|ДК\| =	С ( 6 ; 10; 0)	5) \|ДК\| =
Д ( 5; 4; 11)	6) \|АК\| =	Д ( 5; 4; 11)	6) \|АК\| =
К ( -4; 4; -1)	7) \|АВ\| =	К ( -4; 4; -1)	7) \|АВ\| =
М ( 1; 1; 3)	8) \|ВД\| =	М ( 1; 1; 3)	8) \|ВД\| =
Знайти:	9) \|АМ\| =	Знайти:	9) \|АМ\| =
	10) \|СД\| =		10) \|СД\| =
	11) \|АС\| =		11) \|АС\| =
Дано:	Розв'язування:	Дано:	Розв'язування:
О ( -1; 0; -6)	1) \|ОА\| =	О ( -1; 0; -6)	1) \|ОА\| =
Р ( 7 ; 4 ; -5)	2) \|ОР\| =	Р ( 7 ; 4 ; -5)	2) \|ОР\| =
А ( 5 ; -2 ; 3)	3) \|АД\| =	А ( 5 ; -2 ; 3)	3) \|АД\| =
В ( 1 ; -2; 0)	4) \|ВС\| =	В ( 1 ; -2; 0)	4) \|ВС\| =
С ( 6 ; 10; 0)	5) \|ДК\| =	С ( 6 ; 10; 0)	5) \|ДК\| =
Д ( 5; 4; 11)	6) \|АК\| =	Д ( 5; 4; 11)	6) \|АК\| =
К ( -4; 4; -1)	7) \|АВ\| =	К ( -4; 4; -1)	7) \|АВ\| =
М ( 1; 1; 3)	8) \|ВД\| =	М ( 1; 1; 3)	8) \|ВД\| =
Знайти:	9) \|АМ\| =	Знайти:	9) \|АМ\| =
	10) \|СД\| =		10) \|СД\| =
	11) \|АС\| =		11) \|АС\| =

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

а	р	в	г	д	е	і	б	л	н	п	о	м	ї
12	15	20	11		13	9			14	10	5	7

docx

Завантажити

Зберегти на потім

Додав(-ла)

Джоболда Олена Олександрівна

Пов’язані теми

Геометрія, 10 клас, Матеріали до уроків

До підручника

Геометрія (академічний рівень) 10 клас (Бурда М.І., Тарасенкова Н.А.)

Додано

9 березня

Переглядів

Оцінка розробки

Відгуки відсутні