Елементи ейдографіки на уроках математики
Ейдографіка – особливий різновид комп'ютерного моделювання за допомогою графіків рівнянь. Це своєрідний симбіоз математики, комп'ютера і мистецтва. У статті наведено приклади використання різних типів задач
Значно підвищує інтерес школярів до вивчення математики дидактична гра. Вплив її на школярів проявляється в тому, що гра вносить деякий елемент невизначеності, що збуджує, активізує розум, налаштовує на пошук оптимальних рішень. Використовуючи у навчанні дидактичну гру, вчитель може розвивати у школярів такі компоненти творчих якостей як фантазія, творча уява, образність мислення. Л.В. Тополя, М.Е. Марко виокремлюють наступні притаманні педагогічній грі риси: вільна розвиваюча діяльність, що починається за бажанням учня, заради задоволення від самого процесу діяльності, а не тільки від результату (процедурне задоволення); творчий, в певній мірі імпровізаційний, активний характер діяльності(поле творчості); емоційна піднесеність діяльності (емоційна напруга), що передбачає як суперництво, так і співпрацю в команді; змагання та ін.; наявність прямих чи непрямих правил, що відображають зміст гри, логічну і часову послідовність її розвитку. За характером педагогічного процесу виділяють такі групи гри:
а) навчальні, тренувальні, контролюючі, узагальнюючі;
б) пізнавальні, виховні, розвиваючі;
в) репродуктивні, продуктивні, творчі та інші.
Дидактична гра, що використовується як засіб розвитку пізнавальної активності школярів, є грою за готовими правилами. 
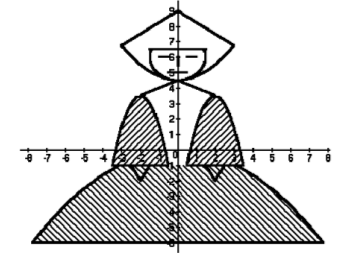У формі конкурсу художників-математиків рекомендують провести заняття побудови графіків функцій і автори електронного посібника «Інноваційні інформаційно-комунікаційні технології навчання математики» (за ред. М.І. Жалдака), [12]. На уроці чи спецкурсі бажано об’єднати учнів у групи і кожній з них запропонувати системи рівнянь чи нерівностей, якими зашифровано малюнок. Переможе та команда, яка краще справиться з побудовою графіків, записаних на аркушах. Побудову можна здійснити як вручну, так і з використанням ПЗНП GRAN1. Виконуючи завдання, учні оперують поняттями області визначення і області значень функції. При розшифровці рис. 29 у школярів можуть виникнути проблеми при побудові залежностей з модулями, а саме – «руки» 
та «рукавів» 
Завдання з тренувального перейде в розряд розвиваючого, якщо запропонувати учням описати рівняннями малюнок, виконаний в координатній площині. При вивченні теми «Побудови графіків функцій за допомогою елементарних перетворень» актуальним буде творчий проект «Малюємо графіками функцій». Кінцевим продуктом в проекті стане колекція малюнків. Завдання для школярів будуть корисними у тому смислі, що закладають базу для усвідомлення практичного застосування матеріалу – опису графічних зображень за методом функціонального подання. Учням доступно вивчати предмет в ігровій формі. При цьому наявний елемент заохочення, ігровий ефект. Школярі мають можливість проявити нестандартний підхід, творчість, розкрити прихований потенціал дослідника.
В окремих учнів можуть виникнути проблеми при створенні малюнка для описування, а не лише при добиранні функцій. Простіше побудувати графік функції за готовою формулою. Інша справа, коли потрібно проаналізувати – графіки яких функцій(чи частини графіків) нагадують ті чи інші криві, дібрати формулу, з’ясувати вплив коефіцієнтів, можливо, зробити корекцію малюнка тощо. Тобто, виконання малюнків створює передумови формування не лише творчої уяви і фантазії, але й таких пізнавальних якостей, як уміння аналізувати, синтезувати, креативної якості – здібності до формування залежності.
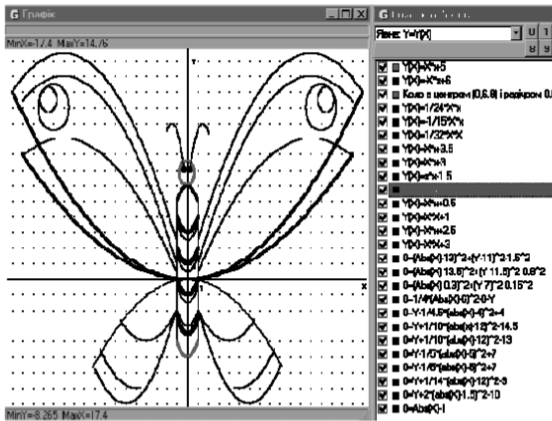
Задачі з ейдографіки
Задачі ейдографіки доцільно класифікувати за домінантним напрямом
перекодування «умова-вимога». За цією засадою можна виділити:
- задачі з домінантним напрямом перекодування «знаково-символьне - графічне»;
- задачі з домінантним напрямом перекодування «графічне - знаково-символьне»;
- задачі, в яких домінантний напрям перекодування постійно змінюється й залежить від типу мислення учня та його індивідуальних особливостей.
Перш ніж проілюструвати сказане прикладами, зробимо кілька суттєвих зауважень.
По-перше, опанування ейдографіки неможливе без досконалої орієнтації на координатній площині.
По-друге, враховуючи специфіку створення рисунків у техніці ейдографіки доцільно оволодіння параметричним заданням ліній.
По-третє, ейдографіка неможлива без знання найпростіших геометричних перетворень графіків функцій, включаючи геометричні перетворення графіків функцій, що задані параметрично.
По-четверте, ейдографіка потребує відповідних програмних засобів. Найпростішими та найефективнішими в даному випадку, на мою думку, є програмно-методичний комплекс GRAN та програмний засіб Advanced Grapher із великими перевагами першого.
У програмному середовищі GRAN кількість графіків функцій, побудованих в одній системі координат, практично необмежена, а в програмному середовищі Advanced Grapher можна будувати їх не більше 20.
По-п’яте, ейдографіка потребує вміння виконувати геометричні перетворення плоских фігур (паралельне перенесення, симетрію відносно точки та прямої, поворот, подібність).
По-шосте, естетичний аспект ейдографіки ґрунтується на знаннях особливостей компоновки композиції, розумінні ролі обрамлення, вмінні акцентувати увагу на певних деталях різними засобами (колір, товщина та стиль лінії). Це царина образотворчого мистецтва й естетичних уподобань учнів.
По-сьоме, учитель та учні мають усвідомити самобутність і неповторність техніки ейдографіки. Тому «від розуміння - через наслідування -до власних творчих здобутків» – тільки такий орієнтир принесе радість самоствердження та відкриття.
Наведемо приклади основних типів задач ейдографіки.
Задача 1 (домінантний напрям перекодування умова-вимога за схемою «знаково-символьне - графічне»). Зобразіть графічний етюд, використовуючи технологічну карту (аналітичне задання).
Таблиця
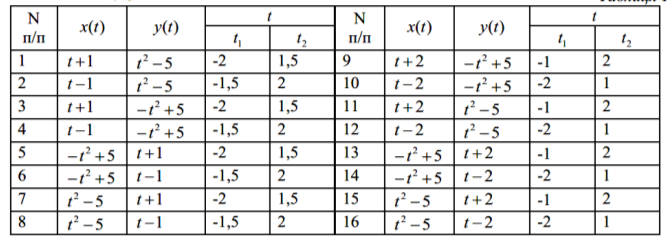
Відповідь наводимо на рисунку без додаткових пояснень. (Рис. 51)
Задачі, на зразок наведеної вище, сприяють усвідомленню аналітичного задання графічного етюда, формуванню навичок роботи з програмними засобами, візуалізації знаково-символьної інформації, забезпечують репродуктивний рівень навчальних досягнень.
Зауважимо, що запропонована технологічна карта може бути доповнена додатковою інформацією щодо товщини кожної лінії та її кольору.
Завдання 1. Вважаючи графічний етюд фрагментом, запропонуйте свій варіант:
а) горизонтального орнаменту;
б) вертикального орнаменту;
в) рисунка, для якого він слугує центром.
Завдання 2. Домалюйте графічний етюд так, щоб він став узором для вишивання серветки квадратної форми тощо.
Наведемо приклади задач другого типу.
Задача 2 (домінантний напрям перекодування умова-вимога за схемою «графічне -знаково-символьне»). Розробіть технологічну карту графічних етюдів, зображених на рисунках 52 і 53 , якщо відомо, що вони створені винятково за допомогою парабол.
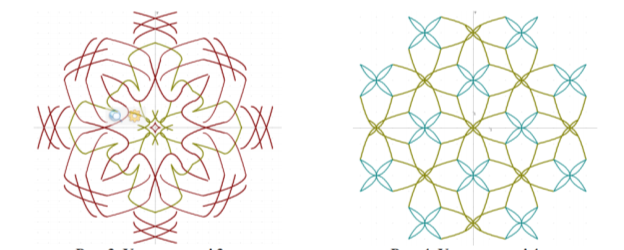
Перша задача (створення графічного образу за його аналітичним заданням) і друга задача (аналітичне задання графічного образу на певному класі функцій) є взаємно оберненими, тому їх поєднання є особливо цінним.
Перша задача простіша й завжди має єдиний розв’язок. Друга задача складніша. Навіть якщо відомий клас функцій, що використовувалися при створенні графічного етюда, задача має частково-пошуковий характер.
Якщо ж клас функцій, що використовувався для створення графічного етюда, невідомий, то задача стає неоднозначною і можливі тільки численні версії, що наближатимуть нас до відповіді.
Найцікавішими задачами, які відповідають творчому рівню навчальних досягнень, є задачі на самостійне створення графічних етюдів та розробку їх технологічної карти.
Уже навіть формулювання такої задачі має певні особливості, а вимоги до її розв’язання стосуються тільки програмних засобів, форми графічного етюда, розмірів, кількості використаних ліній, кольорової гами, наявності певного виду симетрії чи її відсутність, відповідності заданій темі та функціональному призначенню. Учень - майстер має повне право самостійно обирати послідовність етапів своєї роботи, пропонувати авторський підхід до задачі, захищати своє бачення проблеми.
Наведемо орієнтовні формулювання задач третього типу:
- створіть візерунок для гаптування, симетричний відносно осі OY (осі OX, початку координат);
- створіть горизонтальний орнамент для вишивання рушника (вертикальний орнамент для вишивання сорочки);
- розробіть логотип, емблему дитячого спортивного свята (фірмового магазину «Світ дитячих мрій»).
Для тих, хто виявляє особливий хист до ейдографіки і має певні здібності, можна ускладнити завдання:
- проілюструйте казку, оповідання;
- створіть ексклюзивну вітальну листівку (різдвяну, великодню);
- проілюструйте задачу із серії «Жива алгебра», «Жива геометрія» тощо.
Задача третього типу передбачає подовжений термін виконання. Навчально-пізнавальну діяльність учнів можна організувати як роботу над проектом, оскільки задача має на меті самостійне створення продукту, який матиме певну духовну (можливо й матеріальну) цінність.
Таблиця
Відповідь наводимо на рисунку без додаткових пояснень. (Рис. 51)
Задачі, на зразок наведеної вище, сприяють усвідомленню аналітичного задання графічного етюда, формуванню навичок роботи з програмними засобами, візуалізації знаково-символьної інформації, забезпечують репродуктивний рівень навчальних досягнень.
Зауважимо, що запропонована технологічна карта може бути доповнена додатковою інформацією щодо товщини кожної лінії та її кольору.
Завдання 1. Вважаючи графічний етюд фрагментом, запропонуйте свій варіант:
а) горизонтального орнаменту;
б) вертикального орнаменту;
в) рисунка, для якого він слугує центром.
Завдання 2. Домалюйте графічний етюд так, щоб він став узором для вишивання серветки квадратної форми тощо.
Наведемо приклади задач другого типу.
Задача 2 (домінантний напрям перекодування умова-вимога за схемою «графічне -знаково-символьне»). Розробіть технологічну карту графічних етюдів, зображених на рисунках 52 і 53 , якщо відомо, що вони створені винятково за допомогою парабол.
Перша задача (створення графічного образу за його аналітичним заданням) і друга задача (аналітичне задання графічного образу на певному класі функцій) є взаємно оберненими, тому їх поєднання є особливо цінним.
Перша задача простіша й завжди має єдиний розв’язок. Друга задача складніша. Навіть якщо відомий клас функцій, що використовувалися при створенні графічного етюда, задача має частково-пошуковий характер.
Якщо ж клас функцій, що використовувався для створення графічного етюда, невідомий, то задача стає неоднозначною і можливі тільки численні версії, що наближатимуть нас до відповіді.
Найцікавішими задачами, які відповідають творчому рівню навчальних досягнень, є задачі на самостійне створення графічних етюдів та розробку їх технологічної карти.
Уже навіть формулювання такої задачі має певні особливості, а вимоги до її розв’язання стосуються тільки програмних засобів, форми графічного етюда, розмірів, кількості використаних ліній, кольорової гами, наявності певного виду симетрії чи її відсутність, відповідності заданій темі та функціональному призначенню. Учень - майстер має повне право самостійно обирати послідовність етапів своєї роботи, пропонувати авторський підхід до задачі, захищати своє бачення проблеми.
Наведемо орієнтовні формулювання задач третього типу:
- створіть візерунок для гаптування, симетричний відносно осі OY (осі OX, початку координат);
- створіть горизонтальний орнамент для вишивання рушника (вертикальний орнамент для вишивання сорочки);
- розробіть логотип, емблему дитячого спортивного свята (фірмового магазину «Світ дитячих мрій»).
Для тих, хто виявляє особливий хист до ейдографіки і має певні здібності, можна ускладнити завдання:
- проілюструйте казку, оповідання;
- створіть ексклюзивну вітальну листівку (різдвяну, великодню);
- проілюструйте задачу із серії «Жива алгебра», «Жива геометрія» тощо.
Задача третього типу передбачає подовжений термін виконання. Навчально-пізнавальну діяльність учнів можна організувати як роботу над проектом, оскільки задача має на меті самостійне створення продукту, який матиме певну духовну (можливо й матеріальну) цінність.
про публікацію авторської розробки
Додати розробку